Funciones 3ESO

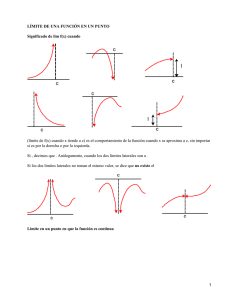
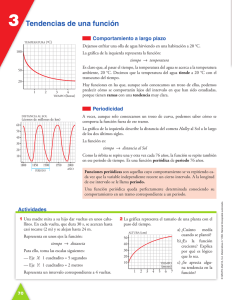
Funciones
3ESO
Una función de variable real es una correspondencia que asocia a cada elemento de un
determinado conjunto de números reales un único número real que se designa como y=f(x)

DOMINIO / RECORRIDO o IMAGEN
Dominio Dom(f) es el conjunto de valores de x para los cuales existe la función.
Recorrido o Imagen Im(f) es el conjunto de valores que toma la función; es decir, es el
conjunto de valores y para los cuales hay un x tal que f(x)=y
No pertenecen al dominio de definición:
a. Los valores que anulan el denominador
b. Los valores que hacen negativo el radicando de las raíces cuadradas o de índice par.

TASA DE VARIACIÓN
La Tasa de variación de una función f(x) en el intervalo [a,b] es:
TV[a,b]=f(b)-f(a)
Se llama Tasa de Variación Media de f(x) en el intervalo [a,b] a:

CRECIMIENTO, MÁXIMOS Y MÍNIMOS
La función f(x) es creciente en un tramo si, siendo x1<x2, entonces f(x1)<f(x2)
Es decir, una función es creciente en un intervalo si para cualquier par de valores en él, a,b
la Tasa de Variación es positiva.
Análogamente, es decreciente en un tramo / intervalo si siendo x1<x2, entonces f(x1)>f(x2)
Es decir, si la TV[a,b]=f(b)-f(a)<0, la función es decreciente en ese tramo.
Una función tiene un máximo relativo en un punto cuando en él la función toma un valor
mayor que en los puntos próximos; en tal caso, la función es creciente hasta el máximo y
decreciente a partir de él.
Análogamente, si f(x) tiene un mínimo relativo en un punto, es decreciente antes del punto
y creciente a partir de él.
La función tiene un máximo absoluto en x=a si f(a) es mayor o igual que el valor de f(x)
en cualquier otro punto del dominio de la función.
f(x) tiene un mínimo absoluto en x=a si f(a) es menor o igual que el valor de f(x) en
cualquier otro punto del dominio de la función.

TENDENCIA
Una función tiende hacia un valor constante k cuando al aumentar x, y se va aproximando
a k. Se dice entonces que “cuando x tiende a más infinito, y tiende a un valor constante k”.
página 1
Dpto. de Matemáticas - colegio NUESTRA SEÑORA DEL PILAR - Madrid
Funciones
3ESO
Una función tiende a más infinito cuando al aumentar los valores de x, los valores de y
también aumentan. Se dice que “cuando x tiende a más infinito, y tiende a más infinito”.
Análogamente, al disminuir la x, y tiende a menos infinito. (Ej: y=ax para x>1)

PERIODICIDAD
Una función es periódica de período T, si para todo x del dominio se cumple: f(x+T)=f(x)
ACOTACIÓN
Una función f(x) está acotada inferiormente si existe un número real k tal que, para todo
x,
El número k se llama cota inferior.
Una función f(x) está acotada superiormente si existe un número real k’ tal que, para todo
x,
El número k’ se llama cota superior.
Un función f(x) está acotada si lo está superior e inferiormente.

SIMETRÍA
Simetría par → una función f(x) es simétrica respecto al eje de ordenadas cuando para
todo x del dominio se verifica:
f(x)=f(-x)
Se dice que existe una simetría par. Ejemplo: y=x2+1
Simetría impar → f(x) es simétrica respecto del origen de coordenadas (0,0) cuando para
todo x del dominio se verifica que:
-f(x)=f(-x); o lo que es lo mismo: f(x)=-f(-x)
Se dice que tiene simetría impar. Ejemplos: f(x)=x3; f(x)=|x|

MONOTONÍA: CONTINUIDAD / DISCONTINUIDAD
Una función es continua cuando no presenta discontinuidades de ningún tipo.
Una función es continua en un intervalo [a,b] si no presenta ninguna discontinuidad en él.
Cuando una función se describe aplicando diferentes fórmulas a distintas partes de su
dominio, se dice que la función está definida a trozos.
El intervalo en el cual se define una función puede ser cerrado, abierto o semiabierto.
Para describir analíticamente una gráfica formada por trozos, se hace:
a. Se dan las ecuaciones de los diversos tramos
b. Enumerados por orden de izquierda a derecha
c. Indicando en cada uno de los tramos los valores de x para los que la
función está definida.
página 2
Dpto. de Matemáticas - colegio NUESTRA SEÑORA DEL PILAR - Madrid