capitulo 1 cuadernillo de 4to

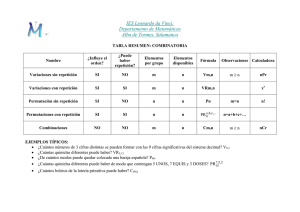
Matemática 4to año TT
Liceo N° 12 DE.8
Prof. Susana Gómez
Capítulo I
Combinatoria y Probabilidad
Los problemas de conteo son aquellos en los que la solución buscada da como resultado
situaciones o conjuntos de muchos elementos. Como agotar todas las posibilidades puede tornarse
una tarea complicada, se buscan estrategias o fórmulas para evitar enumerarlas.
Principio multiplicativo o regla del producto dice que si una elección tiene m posibilidades y otra
n entonces la realización de la misma tiene m.n posibilidades
Ejemplos:
1. ¿ Cuántos números capicúas de dos cifras hay? ¿ Y de tres?
2. ¿Cuántos menúes distintos se pueden formar con 2 entradas, 4 platos principales y tres
postres?
Estrategias para contar
Variaciones y Permutaciones sin repetición
En general las variaciones sin repetición de m elementos elegidos de a n elementos se escribe y
calcula
V mn = m⋅(m−1)⋅(m−2) .... con n factores decrecientes.
Ejemplos:
1. En el Club social del Barrio se realizan elecciones internas para formar una comisión con un
presidente, un vicepresidente y un tesorero. Si se postulan 25 socios como candidatos para
cubrir dichos puestos ¿ De cuántas maneras diferentes se pude armar esa comisión?
En general las permutaciones sin repetición de m elementos se calculan como
Ejemplos:
1. Cinco amigos van al cine. Se sientan en la misma fila y
en cinco butacas contiguas .¿ De cuántas maneras
diferentes pueden acomodarse los cinco amigos?
Pm = m!
Factorial de un número natural n (n!)
es el producto de todos los números naturales
menores o iguales a n.
Por ejemplo 7!= 7.6.5.4.3.2.1.
Se define que 0!=1.
Variaciones con repetición
En general las variaciones con repetición de m elementos tomados de a n elementos se escribe y
calcula
Ejemplos:
V mn = m
n
Matemática 4to año TT
Liceo N° 12 DE.8
Prof. Susana Gómez
1. ¿ Cuántos números de seis cifras se pueden formar con los dígitos del 1 al 9 inclusive?
Actividades
1. Con los dígitos 1; 2; 3; 4 y 5.
a)
¿ Cuántos números de 5 cifras se pueden formar?
b)
¿ Cuántos números de 5 cifras distintas existen?
d)
¿ Cuántos de los números obtenidos en b) son mayores a 20000 y múltiplos de 5?
2. Un grupo de siete atletas corre una carrera .¿De cuántas formas pueden ubicarse en los tres
primeros puestos?
3. Un quinteto vocal ensaya una presentación¿ De cuántas maneras distintas pueden disponerse
uno al lado del otro?
Combinaciones
En general las variaciones con repetición de m elementos tomados de a n elementos se escribe y
calcula
C mn =
V mn
m!
=
= m
n!
(m−n)! n !
n
()
Ejemplos:
1. Para confeccionar una cartelera una profesora debe seleccionar un grupo de tres estudiantes¿
De cuántas maneras puede hacerlo sin en total son 30 los interesados?
2. A partir de un octógono regular se quieren formar cuadriláteros convexos cuyos vértices
coincidan con algunos de los vértices del octógono ¿ Cuántos cuadriláteros se pueden
formar de esa manera?
Números combinatorios
Algunas propiedades de los Números combinatorios:
m!
a) m =
=1
0
(m−0)! 0 !
m!
b) m =
=1
m
(m−m)! m!
m!
c) m =
=m
1
(m−1)! 1!
()
()
()
Ejemplo
Ejemplo
Ejemplo
(70) = 77! 0! ! = 1 Recuerda que 0! = 1
5!
5!
=
= 1 Recuerda que 0! = 1
(55) = (5−5)!
5! 0!5!
6!
6!
6.5 !
=
=
=6
( 61) = (6−1)!
1! 5 ! 1 ! 5 ! 1 !
Matemática 4to año TT
Liceo N° 12 DE.8
Prof. Susana Gómez
Triángulo de Pascal o de Tartaglia
(Investiga su historia y curiosidades del triángulo, visita: http://www.disfrutalasmatematicas.com/triangulopascal.html y http://www.acmor.org.mx/?q=content/tri%C3%A1ngulo-de-pascal )
El triángulo de Pascal o de Tartaglia puede definirse como un conjunto de números combinatorio
organizados en forma simétrica. Estos números expresan entre otras cosas coeficientes binomiales,
pero su utilidad es mucho mayor.
Para construir se pueden usar los números combinatorios:
Otra manera de construir el triángulo, es empezar con "1" arriba, e ir
colocando números debajo formando un triangulo. Con la condición
de que cada número que coloques sea igual a la suma de los dos
números que tiene encima, menos los extremos, que son siempre "1”.
(Aquí está remarcado que 1+3 = 4)
Diagonales
La primera diagonal es, claro, sólo "unos", y la siguiente son todos
los números consecutivamente (1,2,3, etc.)
La tercera diagonal son los números triangulares
(La cuarta diagonal, que no hemos remarcado, son los números
tetraédricos.)
Sumas horizontales
¿Notas algo en las sumas horizontales? ¿Hay algún patrón? ¡Es
increíble!
Se dobla cada vez (son las potencias de 2).
Simetría
El triángulo es simétrico, esto quiere decir que se ve igual desde la
derecha que desde la izquierda
Matemática 4to año TT
Liceo N° 12 DE.8
Prof. Susana Gómez
Usar el triángulo de Pascal
Caras y cruces
El triángulo de Pascal te dice cuántas combinaciones de caras y cruces de pueden salir tirando
monedas. Así puedes averiguar la "probabilidad" de cualquier combinación.
Por ejemplo, si tiras una moneda tres veces, sólo hay una manera de sacar tres caras (CCC), pero
hay tres maneras de sacar dos caras y una cruz (CCX, CXC, XCC), también tres de sacar una cara y
dos cruces (CXX, XCX, CXX) y sólo una de sacar tres cruces (XXX). Esta es la pauta "1,3,3,1" en
el triángulo de Pascal.
Tiradas
Resultados posibles (agrupados)
Triángulo de Pascal
1
C
X
1,1
2
C,C
XC; CX
XX
1,2,1
3
CCC
CCX, CXC,XCC
XXC,XCX,CXX
XXX
1,3,3,1
4
CCCC
CCCX, CCXC,CXCC,XCCC
CCXX, CXXC, XXCC, CXCX, XCXC
XXXC, XXCX,CXXX,XCXX
XXXX
1,4,6,4,1
Ejemplos:
1. Añade al Triángulo de Pascal cuya última fila corresponde a 25 tres filas más.
2. Sin calcularlo mirando el triángulo ¿ Cuánto vale C5,3 , C5,4 , C5,2, C5,5.
Binomio de Newton
Vamos a calcular las sucesivas potencias de un binomio
¿Te animas a calcular (a + b)5 sólo observando?
Pista: Fíjate que siempre aparecen todos los posibles términos del grado que estamos calculando. por lo que para calcular la quinta
potencia tendremos. Para los coeficientes fijate la relación con el triángulo de Pascal.
Podemos escribirlo también utilizando números combinatorios:
Matemática 4to año TT
Liceo N° 12 DE.8
()
Prof. Susana Gómez
()
()
()
()
()
(a+b)5 = 5 a5 + 5 a 4 . b + 5 a3 . b2 + 5 a2 . b3 + 5 a1 . b4 + 5 b5
0
1
2
3
4
5
Otros problemas de conteo.
Problema 1
Dados 10 números naturales consecutivos cualesquiera, hallar su suma. Encuentren la expresión
general.
Problema 2
Encuentren una fórmula que permita determinar el total de diagonales que tiene un polígono de n
lados.
Problema 3
Analicen si es posible que la suma de 10 números consecutivos de por resultado 735 245. En caso
afirmativo determinen que números se han sumado. Justifique.
Actividades de repaso
1. Julia tiene 7 témperas de diferentes colores ¿Cuántas mezclas de tres colores se pueden
hacer? ¿ y de dos colores?
2. Consideren las letras de la palabra POTENCIA y determinen cuántas palabras de sies letras
con y sin sentido se pueden armar.
a)
¿Cuántas comienzan con P?
b)
¿Cuántas terminan con N?
c)
¿Cuántas empiezan con la sílaba PO?
3. En una fábrica 18 empleados deben realizar su trabajo organizándose en tres turnos rotativos
de igual cantidad de personal. Determinar de cuántas maneras distintas pueden distribuirse
para cumplir con su horario de trabajo.
4. Un chef tiene 8 especies aromáticas y desea seleccionar 3 para condimentar un nuevo plato.
Determinar la cantidad de elecciones que puede hacer.
5. Estudien cuáles de las siguientes expresiones representan números pares, para cualquier n
natural.
2
a) 3. n +1
b) (n+1).(n−1)
c) n3 −n
d) n(n+1)
6. Considere que n personas asisten a una reunión y todas se saludan con un apretón de manos.
¿Cuántos apretones de mano hubo? ¿Si hubo 45 apretones de mano cuantas personas hubo?