PDF (Parte 2)

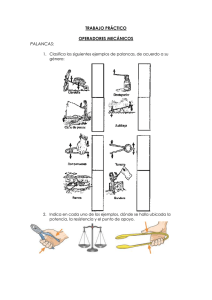
CAPITULO IV. TEORIA
1. DISEÑO POR RESISTENC
1.1.
Introducción
En el campo es común ver p
de máquinas que fallaron es
de cargas estilticas o cargas
que indican la necesidad d
principios que rigen el disefl
su mejor desempeflo. Lo idea
los resultados de los ensayo
elegido para el diseflo. Si sob
o de torsión o cargas combin
resultados de los ensayos
además de las condiciones
trabajo, acabado superficial
ensayos, es frecuente que l
utilicen los valores de resiste
diferentes materiales o el ap
tema, siempre y cuando la fa
vida humana o cuando el vo
regla general cuando sobre l
material es dúctil no se ne
esfuerzo en el análisis o disei
como tal, se hace necesa
concentración del esfuerzo Kt
Las teorías de falla han sido
carga estática y materiales i
condiciones de carga como im
l.2. Teoría del esfuerzo norm
que la faI1H se produce cuan
es igual a la resistencia. Si l
02 > 03 (esfuerzos principal
entonces:
Donde: St
Se
=
Resistencia de
Resistencia de
En el caso de materiales frági
CíI
==
Sut
o
Donde:
SU! Y Suc son
compresión, respectivamente
Esta teoría ha sido encontra
como frágiles. Teniendo cn c
las resistencias (Sut y Suc)
hipótesis de falla del esfuer
fuera del cuadro del diagram
s uc
Figura 22.Diagrama de esfu
normal máximo.
1.3. Teoría del esfuerzo corta
En materiales dúctiles predic
5'
'll1áx :;:, - )
o Cíl
Cí3 :;:, S\,
2
Los esfuerzos cortantes princ
2
2
2
2
Como 1:mi'tx no puede super
(Figura 23) por 01< (Sy/n)' y
teoría del esfuerzo normal m
Figura 23. Hipótesis del esf
Además establece que la res
por: Ssy = 0.50 Sy. Hay segu
=
t
Olax
±)(Ol 2
-O~2.12
.Sg.
Sv
)
2n
~
Las rectas de frontera serán
1.4. Teoría de la fricción in
No todos los materiales ti
tensión iguales a sus valore
los valores de estas resisten
de la teoría de Mohr conocid
establece:
.93
St
Se
1
Siempre que
al
cantidades positivas. Para
predice mediante: al Sr, a
En las ecuaciones 4.6 y 4.7,
a la fluencia (Sy) o la resis
muestra la hipótesis de la te
de esfuerzo biaxial.
Figura 24. Gráfica de la f
Coulomb- Mohr.
1.5. Teoría de la energía de d
Conocida también con el nom
teoría de vonMises-Hencky
establece que para el estado
o esfuerzo de vonMises ((J.) p
2
y se prevé ocurrirá la fluen
esfuerzo biaxial, (J' se reduce
Si ay ,
(JI'
Y Txy son obtenido
Si solamente
(J,
y
están
Para casos de torsión pura:
0.577 Sy. La ecuación (4.1
el interior de un volumen
producirá el fallo de la pieza
biaxia1 viene dada por una e
- 0
Figura 25. Diagrama de la e
1.6. Caso de materiales dúc
1. Para el caso del diseño
precisión se puede emplear
(TECM). Así mismo, cuando
han de ser altos o cuando
tamaño de una pieza. Esta t
2. La teoría de la energía de
caso de rediseño de piezas,
falla real ele un elemento m
seguridad son estrechos. Es
1.7. Caso de materiales frág
Estos materiales se caract
fluencía, la resistencia a la
que la resistencia a la tensi
(Ssu) es aproximadamente
teoría del esfuerzo normal
Mohr resultan aceptables pa
2. FALLA POR FATIGA
2.1. Introducción
Hay cargas que ocurren
máquinas
que producen
alternantes o fluctuantes
fatiga. Bajo esta condició
esfuerzo máximo menor q
por debajo del esfuerzo d
después de un determina
característica más notab
esfuerzos se repitieron m
FALLA POR FATIGA.
Por lo general una falla po
y propagación de grietas,
crítica de fractura súbita
grieta generalmente se des
en el material, tal como u
cunero o chavetero, un
esfuerzos, tos que fre
superficie.
Frecuenteme
observa una zona de SU
marcas ondulares conocid
áspera de fractura sú bila
y total y por tanto peligro
de fallas es más complejo
La teoría más exacta cono
falla por fatiga se conoce
deformación". Su aplicac
que conlleva a incertidum
La fatiga se aborda de
aplicación:
Diseño para una vida infi
debajo del límite de agua
esfuerzo por debajo del c
aplicaciones, los ciclos se
resulta el único enfoque
atraviesa por un ciclo cad
engranaje. Si gira a 4000
cuarto de millón durante c
Diseño para una vida se
diseño de tal forma que la
ocasiones una
catástrof
reemplazarse el componen
vida que causarú que un
empiecen a presentar griet
Diseño tolerante al da
fabricadas ya pueden tene
entonces en la vida de cre
pudiera pasar inadvertida
2.2. Curva de fatiga S-N
esfuerzo)
Frecuentemente
en
en
experimentalmente el núm
fatiga) correspondiente a
cíclico bajo ciertas condic
grafican, obteniendo un d
empleo de papel logarítmi
curva. Estos diagramas (
pruebas de ensayos con p
en particular.
En el caso de los aceros se
punto no ocurrirá falla.
qu iebre se denomina límit
metales no férreos y s
resistencia a la fatiga.
E
como: Fatiga de ciclo bajo
correspondiente a N > 10
región de duración finita
localiza entre 10 6 Y 10 7 ci
permite escoger el método
la resistencia.
lO~
Numel
Figura 26. Diagrama S N
pruebas de fatiga axial con
2.3. Limite de fatiga o limi
Mischke, analizando much
que el límite de resistenc
realidad con la resistencia
relación es:
0.504 Sut
S'e =
100 kpsi
{
700 MPa
Resistencia última
Limite de resisten
vejiga de rotación
Se - . . Limite de resiste
máquina particula
2. 4. Resistencia a la fatig
En el diagrama S
N (Fig
bajos hasta N
10 3 la ecu
escribirse: log Sf o: log a+b
Esta recta cortará 10 6 ci
Sustituyendo estos valores
(O.9Sut)2
a
b=
S'e
1
--IOg
3
Si se tiene un esfuerzo co
de ciclos de duración N co
la ecuación (4.14), sustituy
La constante a depende
unidades MPa (N/mm2) o k
ecuaCIOnes.
2.5.
Factores que modific
Marín, ha propuesto una
modifican el limite de fatig
propuesto la ecuación: (4.1
Factor de
superficie
Factor de
tamaño
Facto
carga
Cuando no se dispone de
estimaciones se hacen ap
slgue:
•
Factor de Superficie (k
La superficie de la probeta
pulida. Los factores de mo
acabado y de la resistencia
para diversos acabados:
IJ
Ka=aSut (4.18); en donde S
a y b depende del acabado
4.1.
Tabla 4.1
Parámetros a
Acabado superficial
Esmerilado
MHquinado o estirado en
Laminado et1-~ca-·l·-íC~.l~1t··-~e·~-·---
Como sale de forja
Factor de tamano (kb).
tamaño, o sea que kb =
d
0.3
yOl07
j
0.1
i
_d_y
( 7.62 J
OI07
2.79
Para tamaúos mayores se
torsión.
Cuando se utilizan seccion
de la dimensión efectiva
volumen del material some
del esfuerzo máximo con el
rotatoria.
Dependiendo
diámetros equivalentes:
• Para una sección redo
de=d
• Para una sección redon
• Para una sección recta
0.808 (bh) 1/2
•
Factor de carga (kc).
o.. 923
kc =
l
1
1
0.577
• Factor
carga axial
carga axial
flexión
torsión y cor
de Temperatu
investigar la relación e
temperatura debido
disminuye con rapidez
el límite de resistencia
temperatura del lugar
ST/ SRT, en donde ST
temperatura de operac
temperaturas elevadas p
o debido a una combin
dar lugar a la corrosión
temperatura, originando
la fatiga del material.
• Factor de efectos divers
hay otros factores que
fatiga o lo mejoran.
Hay operaciones como
laminado en frío, que
superficie de la pieza
limite de resistencia
trabajado en exceso,
el g
ori
y a
a l
Corrosión. Se espera que m
corrosivos, ocurra una dism
fatiga (Se), El problema no
esfuerzos repetidos se p
problema del diseilador es
afectan la duración a la fat
Los recubrimientos metáli
niquelado o camizado red
galvanizado (revestimiento
fatiga,
Concentración del esfuerzo
ecuación:
kf = 1 + q (kt
1) q: sensibilidad de la muesca
(para aceros entre O y
utilizado) .
1; sie
kt: factor de concen tración de e
Como factor de reducción de la
el enfoque: ke = 1/ lkf 2.6.
Esfuerzos fluctuante
(d
Figura 27. Esfuerzo fluctu
En general un esfuerzo flu
constante varía con el tiem
• Ciclo de esfuerzo: el
esfuerzo - tiempo el cua
• Esfuerzo máximo (Címáx
ciclo de esfuerzo.
U
positivo y una de compr
• Esfuerzo mínimo (Címín
ciclo de esfuerzo.
• l<-:sfuerzo medio (Cím):
máximo y el esfuerzo m
+ ()min
Cím =
2
• Amplitud del esfuerzo
en el esfuerzo máximo
esfuerzo.
Cía =
(J m;íx
(Jmll1
2
• Intervalo de esfuerzo
esfuerzo máximo y e
esfuerzo. ar == amiíx -1:min
• Relación de esfuerzo (R
mínimo y el esfuerzo má
• Cuando Cím
0, el esf
inversión completa y de
Címáx = Cír
• Vida de fatiga (N): N
deformación requerido
por fractura o por creci
2.7. Resistencia a la fatiga
Primordialmente la resis
establece para ciclo de e
medio igual a cero (Gm
aplicaciones en las cuale
superpuesto al esfuerzo
presentan cuatro criterios
Soderberg, de fluencia y
esfuerzos medio se muest
a la fluencia a la tensión
tensión (Sut]
.
Lmea de Sod
o~--------
O
Es
Figura 28. Diagrama de fa
Se ha encontrado expe
esfuerzo medio de tracció
en términos de la amplitud
Varias relaciones se han p
la fatiga correspondiente
base en la resistencia a
cero para un mismo núme
cuatro criterios de falla
ecuaciones, que para el c
en forma de intersecciones
Estas ecuaciones son:
Relación de Solderberg:
t
~~I~:~I t
~~I~~~I
0<1
0
Se
S
.' -+
Relación de Goodman:
Gil
-\­
Se
Gm
Sut
Relación de la línea de f
~+_Sm =J -L
Syt
Syt
I
n"<1
+~=
Syt
Syt
Relación de Gerber:
Una varilla
duro UNS C27000, con u
Para cada estado de esfu
seguridad mediante la
(TENM), la teoría del es
teoría de la energía de dis
MODELO 1.
a) Ox = 70 MPa, Oy =
b) Ox
70 MPa, cxy
-10 MPa,oy
e) Ox
d) Ox
50 MPa, Oy
3
-
a) Omáx = 70 MPa y cmáx =
CY' = [(70)2 - (70)(30)+(30
TENM: n = 310/70
=
TECM: n = (310/2)/35 =
TEDD: 11. = 310/60.8
=
b) o' =81.1 MPa, 0 2= 11.1
cmilx = 46.1 MPa
[81.1)2- (81.1) (-
==
(J'
87.2 MPa
(J'
TENM:n=310/81.1
TECM: n
(310/2)/46.1
TEDD: n = 310/87.2
el
4.1 MPa, 02 == -74.
39 1 MPa
=
(J'
'Cmáx
(J'
= [(4.1)2 - (4.1)(-74
a'
=
76.2 MPa
TENM:n=310/74.1
TECM: n
(310/2)/39.1
TEDD: n == 310/76.2
d)
(J'
(J'
=77.7 MPa,
==
[(77.7)2
7.7
(77.7)(-7
a' ;= 81.8 MPa
TENM: n
TECM: n
TEDD: n
=
==
310/77.7 == 3.
(310/2)/4.27
310/81.8;= 3.
La barra m
aeero UNS G 10350 estira
psi), de 1/4 de pulgada de
se invierte por completo
infinita calcular el fac
trabajando la barra.
MODELO 2.
1000lb
Se ticne: .:.
•:.
.:.
.:.
Esfuerzos completamcn
Carga simple
Sección transversal no
Vida infinita
Se presentan dos puntos
aguJero.
1. Cambio de sección: Se trata de esfuerzos com
1000lb _= 2667
(1.5'")(.0.25")
p
Límite de resistencia a la
Se
==
ka kb kc kd ke
).>
ka: Factor
h
ka = aSut
ka
superfic
~¡
aSut
0
).>
kb
Factor de tamaií
de tamé1l1o y se consid
).>
kc ==
0.923
Factor de carga.
~ kd
~ ke
Factor de efectos
sometida a ten sión sim p
Factor de temperat
r
D=2.25 =1.5
d 1.5"
kt
kf
kf
=
ke
=
=
d
1.95
l+q (Kt-l)
1.713
1
kf
1.5"
=
1+0.75(1
~_1_
1.779
ke == 0.583
Por lo tan Lo :
Se 0.845 x 0.923 x 0.9 x
S'e = 0.504 Sut, si Sut <::; 20
S'e == 0.504 x 80 x 10 3 psi
Entonces: Se = 16500 psi
16500
Por 10 tan Lo: n= - - - = 6.18
2667
de sección).
2. En el agujero
(Ja ==
Se
ka kb kc kd ke S'e
);. ka:
ka
=
0.845 (estira
);.
kb
1 (carga axial: ut
efecto de tamaüo).
0.923(cargaaxia
:Y
kc
>-
kd == 1 (no se dice nada)
);.
ke: d=0.75==0.5
w
1.5
kt =
kf
1 + q (K t - 1 )
kf
1885
1+0.75(
ke
=
0.53
Se
=
0.845 x 0.923 x 0.53
n
16666psi
5333psi
n= 3.12, que es el factor
barra.
El eje mostr
mientras la carga que act
eje es maquinado a partir
psi, Sy = 60.000 psi). Si la
para producir falla por fa
deberá ser el valor de F pa
MODELO 3.
Se trata de un eje con ca
alternos y con sección tra
el efecto de las fuerzas co
el eje es el momento flec
parte inferior de la figura.
La sección crítica del eje
sea menor.
Las pos
probablemente ocurra una
~B
A
-2"----
.....--f---1r--!" ____
/'\----
1 R I
F/21b
16
•
A
Sección B:
Se = ka kb kc kd
(
• Ka
2.70psi (90kpsi
•
í
kb
\
C,13)-O.1131
O
.
0.87
•
kc = 1.0 (flexión)
• kd = 1.0 (no se dice n
• ke: = tratándose de ca
modifícativo por con
de resistencia y no c
o
1.
el kf
Se
=
r
,d
0.0625"
1"
1+0.75(1.9 1)
1.675,
1"
1.25
0.82 x 0.87 x 0.6 x 0
Oa
== M
Z
=
0.5Fx32
n(l")'
=
5.09F
n== S_~ == 3814%
o"
Sección por C:
ka
kb
kc
kd
ke
==
==
==
==
==
0.82
0.85
kel == 1.0
1.0
1.0
Entonces:
Se == 0.82 x 0.85 x 0.504 x 9
1.5Fx32
= 7.82F nx(1.25):J -----
n == Se
=
o"
316 16 ,~ 4043/
7.82F
lF
Sección por D:
ka == 0.82
_ ( el J-O.II.13 _( 1 J-0.II.33_
kb -- - - - 0.3
0.3
kc == kel == 1.0
l:? = _1.~?" = 1.25' ~ = ~.125" = 0.
el
1"
'el
1"
kf == 1 + O. 7 5 ( 1. 7 - 1) == 1. 525
ke == 0.66
Se == 0.82 x 0.87 x 0.66 x 0.5
Oa
==
32(F)
n(1.0):J
=
10.18F
n == 21357 -209%
10.18FF
Sección por E:
ka
=
0.82
(1
kb
),\\,0.11 1 .1
0.85
= . --:- J
\ 0.3 /
kc
Kel
ke '.
D
d
1.0
1.25" ~'1 ~ 2'-.
r
;::),
1"
d
=
0.1
--
kf = 1 + 0.75(1.54-1)
Se
=
0.82 x 0.85 x 0.71 x 0
n
Se
era
n
22447 =4410/
5.09F
/F
; () a
32xO.5F
n(1)1
5.
El análisis anterior mue
ocurriría por la sección
aplicar para que no ocurra
10.18 F
F
2
2098 l
El eje most
fluctuación de torque indi
eje es acero con Sy = 135 k
eje es acabada por rectifi
de
ridad con el cual
10 3 ciclos.
MODELO 4.
Se trata de carga simple c
finita. Aunque el problem
determinar como si el pro
determinar primero la secc
Cambios de sección:
Se: ka kb kc kd ke 0.504
ka = 1.34 (152)·0085 == 0.87
1" ,.0113'
kb ==
)
0.872
\ 0.3
kc
0.5
(torsión)
kd
1.0 (no se dice nada)
í
ke: D
1.5"
1"
d
q
1.5 ;
r
0.1
d
1"
0.75
kf== 1 + 0.75 (1.45-1)
kc == 0.746
Se 1.3
0.874 x 0.872 x 0.57
.:. Se == 25131 psi
Las cargas serían:
Tmáx
=
d/
Tmáxx /2
16x8000(l
TTd~
n(1,,
32
r m1n Tmin x16
TT( 1")
Por lo tanto:
16x2000(lb ~
n( 1
1m
=
"r'
+ r mm
2
-
f"'i
2
y
infinita
u
1 La
1m
modificada:
n Se Sut Para
1
vida
15279psi
..
+ 25465psi
23245psi
152000psi n
En el agujero:
• ka
• kb
0.874 (rectificaci
0.872 (también d
=
• kc
0.577 (eje sometid
• kd = 1.0
(no se dice
• ke:
a
= 0.0625"
kts
OJ)625
1"
d
1.74. (Anexo 2)
=
Para r
(1 ()(
=
2')"
~=--- = 0.03" ,q
kf=1+0.75 (1.74 1)=1.555
ke=0.64
Entonces:
0.874 x 0.8
Se
21560 P
Cálculo de cargas:
tmáx
Ineto
tmáx =
8.0001b-pulgx
--nxO.94[
Tr
Jnefo
.!nefo = ll'A(D
4
d
4
)
32; enton
2000lb-pulgxO.5pulg
... -........... - - - - 0.09pulg 4
43344p
Por lo tanto: Tm
tmin
=
Ta '" 16254 psi
Para vida infinita:
n
n
==
16254
-
+
19674
:=
27090
-­
152000 1.0, lo que muestra qu
Vida finita para el agujero
Sf
= aNb ==>
Sf
=
(O.9~
Se
b -_
J log
a
3
951.2 (50.000)·O.2R
1 Ta
n
Sf
Así:
-1
4
Tm
Su
16254
n
27090
+----­
45980 152.000 <::====J
PROBLEMAS
n
1 .9
1. Una barra laminada e
flueneia mínima en te
Determine los factores
aplicable, en relación c
a) Cí x
10 kpsi, Cí y
-5k
b) Cíx := 12 kpsi, 1xy := 3 k
el 0x:= 4 kpsi, 0y := -9k
d) Cíx
9 kpsi, Cíy
4k
e) Cíx = 15 kpsi, 1xy
5
2. Una barra tiene una re
Determine los factores de
aplicable para:
a) Cíy:=
80 MPa,
1xy
b)
C'ix
= 180 MPa,
e)
C'i x
=
d)
exy
] 40 MPa,
150 MPa C'i y
eXY
3. Determine los factores
la
Energía de disto
esfuerzo en A y B mo
barra es de acero AISI
las cargas F
0.60 KN
'f
J
z
4. La figura muestra un
cojinetes Ay D con pol
bandas son mostradas
que actúan sobre las p
fundido ASTM de grad
tener el eje?
5. Si se vuelve a dise
reduciendo a la mitad
especificaciones, cuál e
CAPITULO V
1. INTRODUCCION
Los ejes, árboles y husos so
en las máquinas y puede
compresión, flexión y torsión
Los ejes o flechas se encuen
mecánico. La mayoría de el
flexión y torsión combinada
de esfuerzos, consistiendo
fatiga. La velocidad de trab
a una velocidad crítica, pue
geometría de un eje, es por
poleas, cojinetes y engranaj
tiene que prever que allí se p
Se debe tener en cuenta qu
específico de un eje se hace
punto sin requerirse la geom
diseí10 de ejes se localiza
cumpliendo los requisitos
determinar, conocido el ma
cuenta los análisis de esfu
aplicables.
2. DEFINICIONES
Eje móvil o simpleme
generalmente de seCClOn
transmitir movimiento y pot
como, engranajes, poleas, vo
Eje fijo: es un elemento
movimientos y ql;e se utili
ruedas, poleas, rodillos y otr
Arbol: sometido primordialm
potencia con polcas, engran
afectados también por la fl
ejemplos típicos.
Husillo: un eje móvil corto
herramienta para realizar
portabrocas en un taladro
en una fresadora.
Siempre que sea posible
mantenerse cerca de los co
movimiento flexionante y p
el esfuerzo por flexión.
Los ejes móviles, por lo gen
mediante el ensamble, cha
cuña o chaveta que entra t
Otros casos donde el proble
puede usar: tornillos de fi
conectores rasurados.
3. DISEÑO PARA CARGAS
Cuando las cargas so
dimensiones de un eje e
cuando las cargas son din
un eje redondo macizo de
flexión, axiales y de torsión
Esfuerzo de flexión
(Las componentes de
para el análisis)
a
32M
=-~+
x
TTd 3
()x
p
4F
TTd¿
Esfuerzo de torsión:
r
xy
16T
TTd
=--3
Utilizando el círculo de
esfuerzos principales no n
Estos esfuerzos
cortante máximo
pueden
cmAx
y el e
f)2 lY~
[l 0;_ + T~y
a =(0 A 2_0 A o B +0 8 ;>\1/ 2 =(0 2
1/,
f
I
X
Reemplazando (5.1) Y (5.2)
4
I
a
c-
2
TTd3l(8M + Fd) + 48T
Con (5.6) Y (5.7) se puede h
d cuando se conoce el valo
Si el análisis o diseño se ha
máximo, entonces:
f adm
=
n
S
= 2n
; Con (5.6)
conoce d o hallar d si se con
Si el diseño se hace por
esfuerzo van Mises admisibl
En muchos casos la comp
puede ser despreciada.
- Teoría del esfuerzo cort
Teoría de la energía d
4. DISEÑO POR FATIGA
En cualquier eje rotatorio
flexión y torsión actuarán
invertidos, permaneciendo
esfuerzos se expresan:
Esfuerzo alternante:
Cí xa
=~2~
TT
Y esfuerzo medio o esfuerzo
1
Si se considera Se como
completamentc corregido y n
Se
n
32M
TTd
a = - 3-a
xa
Si utilizamos el criterio de
afecta cllímite de fatiga a la
11
(32M n \/3
d ==
l-a_-I
TTSe
J
Estos dos componentes de
el CÍrculo de Mohr para cad
esfuerzo cortante o la teoría
obtencr valores equivalente
seleccionarse una de las r
Diagrama de fatiga (Teorías
línea Goodman, Curva Ge
Curva de Bagci).
Con la teoría del esfuerzo c
daño y con la teoría de la e
la resistencia.
Si se utiliza la T.E.C.M, las
ITa
y
= 2Ta
Si se emplea la
E.D.D., l
y
En ejes de transmisión es c
combinación de torsión con
sigu ien tes expresiones:
Si se requiere diseñar d:
d=
{~r(~?~
TT
l"
r í r] ¡
SSY )
+
M
y;
J
\ Sse /
Para la T.E.C.M. donde
=
Si se emplea la T.E.D.D. Ssv
] }3
1
0
Para el caso general en q
contienen una componente
T.E.C.M:
5. FORMULAS BASICAS D
FATIGA
TEORIA
FO
Soderberg
no
Goodman
--
Se
nO
Se
Gerber
nO a
Se
Elíptica ASME
(l~Oa
Se
Bagci
Flueneia (Langer)
n
~····~
S
y
(a) Considera la posibilida
(11 no requiere ser usad
(b) No considera flueneia
enfoque se usa (b) y (11
(e) Cuando ha de realizarse
(d) Se aplica sola. Pero se
flueneia plástica en la
(e) Se aplica sola.
MODELO 1.
Determinar los factores de
en A y B del eje empotrado
teoría de la energía de disto
UNS G 10060 estirado en frí
0.55KN, P = 8.0 KN Y T 3
z
Elemento A:
z
En el circulo de Mohr: a 1
9
Utilizando la T.E.D.D. con S
n=Sy
01
~~~?a
::: 2.8
100.98MPa
Si se utiliza Sut
Elemento B:
330MPa,n
y
=
1: xy =
En el circulo de Mohr: 01
=3
Utilizando la T.E.D.O. con S
01
(37.68)(-12-2)
N = Sy/crl ::: 6.22
Con Sut ::: 330 MPa se obtiene
MODELO 2. Calculo de un e
Un eje recibe una potencia
a de 50 cm de diámetro, de
10 indica la figura. El 60%
un engranaje C de 40cm d
otro engranaje O de 30 cm
ángulo de presión 20°. En
ser fabricado con un acero
2
y Su = 4.000 kg/cm , con c
Determinar el diámetro del
código ASME y usando kf=1
•
Cálculo de los momento
72574,65x36HP
400RPM T -----""----A-
6531,7
72574,65xO.6x36HP
_...
_---"
400RPM
= 72574,65xOAx36HP
o::
39
26
400RPM
•
Cálculo de las fuerzas de
Se supone para la correa qu
la fuerza impulsora neta, o
FA =2F= 2x6531,71
25em Te
= 52
3919,03kgem
.... _ - - - ­
195,
2gem
~
Re
Nc =
xtg200
71,32kg
En una transmisÍón por co
tirante F1 es mayor que la f
10 tanto el sentido de giro de
muestra en la figura.
A continuación se muestra
sobre el eje, siendo RB y RE
Las fuerzas en el plano verti
Ay::: FA sen45°
Cy
369.48 kg
-Fccos30o - Ncsen30::: 205
Dy ::: -FDcos30o + ND sen300
== -11
Para hallar las component
respecto al punto E, así:
369.48 kg (30 cm +30 cm +
cm) - 205.35 kg (44 cm + 32
Despejando: By
-290.85 k
Sumatoria de fuerza en el ej
369.48 kg- 290.85 kg
Ey
=
205
245.86 kg.
El diagrama de fuerzas co
plano yz, es como se mue
kgcm, Mey 13443.3 kgcm y
Las fuerzas en el plano horiz
Ay=369,48
k:s
30_--:*-_
z+-____~====~===
369,48 k¡;;
r~-----'
'--_ _
r...rBy= 11OE:4,4
A
k:s
cm
Calculo de Bx y Ex:
-369.48kg (30 cm + 30cm +
cm) + 36.21 kg (44 cm + 32 c
Despejando: Ex = 490.94 kg.
-369.48kg + 490.94 kg + 36.
Ex 15.69 kg.
Los respectivos diagramas
flexionantes se muestran e
kgcm, Mcx = 7440,6 kgcm y
flexión resultantes en los pu
15675,7
78R3, A
El punto críticu está en B, y
de flexión. Se calcula enton
B y éste será el diámetro pro
<;:---
30 - -*--30
z~____~========
Ax=369,48 kg
157,6
121,46kg¡
A
B
'\
~IC
MBx= -1
Según el código ASME, el es
es el menor entre los dos val
Ss 0.30 x Sy = 0.30 x 3000
Ss 0.18 x Su = 0.18 x 4000
Como existen cuñeros en el
Ss 0.75 x 720 kgj
= 54
Utilizando la formula recom
diámetro para el punto B así
.5x15675, 7)" + (1
dn= 6,21 cm, que es el diáme
PROBLEMAS
1. Un eje circular macizo tr
300 rpm, de forma que
constante. Su longitud e
una resistencia a la fluen
transversal G l 8 (10 4 ) N/
eje considerando un coe
problema aplicando tre
cortante máximo y energí
2. Un eje circular hueco d
debe transmitir un par
tangenciales no deben su
es la mitad del exterior.
torsionado por el eje.
3. Una barra de sección cir
una carga P en el otro ex
par torsor T. La barra
resistencia fluencia Sy =
extremo libre es de 2000
tiene una longitud de 13
2. Calcular el diámetro m
la teoría del esfuerzo cor
distorsión. Despreciar l
cortante.
4. Un árbol rotativo está h
estirado en frío de 42 x
diámetro taladrado en l
Calcular el factor de segu
y estática cuando el á
completamente invertido
flexionan te completamen
5.
Un eje voladizo de acero
carga que varía de -F a
puede soportar el eleme
coeficiente de seguridad
el factor de concentra
sensibilidad a la entalla
es q :oc 0,9. Hacer el análi
Usar: Su 551.2 MPa, S
pulgada y Se 250 MPa
6. y
Un eje de una máquina
cojinetes A y B separad
figura. Se suministran a
mm de diámetro, localiz
La potencia se transmit
cilíndrico de 203 mm de
del cojinete A. La correa
la horizontaL La polea
volante de inercia. La re
de la correa es 3: 1. Los
de presión de 20° y se a
vertical del cje. Si el ma
resistencia de rotura Su=
31 MPa, determinar el d
coeficiente de seguridad e
CAPITULO VI. VIBRACIONE
1. INTRODUCCJON
El análisis de la vibración y
importantes e integrales de
Establecer un modelo matemá
de las soluciones e incorpo
prueba, evaluación y mante
conocimiento de los principios
El estudio de las vibraciones
los cuerpos y a las fuerzas
ingeniería que poseen masa y
movimiento relativo. En gen
disipada y en muchos casos
cierto en la mayoría de las
producen ruidos, afectan las
movimientos indeseables.
Hay dos clases de vibracion
ocurre cuando un sistema osc
propio sistema, esto es no exi
una o más de sus frecuenci
lugar bajo la excitación de fu
el sistema es obligado a vibr
coincide con una de las frecu
una situación de resonancia
grandes. En la práctica, la
gradualmente, al vencer la
movimiento y el cuerpo, final
producida se dice que es amor
2. SISTEMAS DE UN GRADO
2.1 Vibración libre
Un sistema de un grado de
Consiste de una masa m co
amortiguador con coeficiente d
La rigidez k es definida com
deflexión y el coeficiente de
suministrada por el amortigu
velocidad. Si la masa tiene u
de su posición de equilibrio. L
mx + C X + kx
O
Figura 29. Representación de
Donde x es medida desde la po
variables representan las
Sustituyendo una solución de
obtiene la ecuación característ
ms 2 + cs +k
O
Las dos raíces ele la ecuación c
S =t,úJn ± i(,)n (1
Donde
(k/m) y, es la frec
(,)n
t,
=
clCc, relación de am
ce
2 mW n es el coeficie
t = ..y.T
Dependiendo de los valores de
a) Sistema no amortiguado (
ecuación son:
±
s
tú)n
± i(kl mfi2
La solución correspondiente es
x
=
Acoswnt + Bsenwnt
Donde A y B son consta
condiciones iniciales del movi
XI) y la velocidad inicial es I'{
ecuación (6.5), es posible reso
solución es:
x
Siendo Wn la frecuencia natu
(rad/s). La frecuencia natura
Donde fn se expresa en ciclos
una oscilación es p
l/fn = 2r
La solución dada en la ecuaci
la forma x = Xcos(wn-O)
Donde:
r
x
O ta
El movimiento es armOl11CO
ecuación (6.9) y gráficamente
1.0
L...-~
_______
Figura 30. Vibración libre de
diferentes valores de amortigu
b} Sistema subamortiguado
amortiguamiento es me
solución es:
Donde:
(ad
(Vll
(1
1/2
úJd frecuencia natural amorti
que dependen de las condicion
y velocidad inicial Vo:
Puede ser expresada en la form
x == [exp( ~~(,)n t] XCOS((,)d t - O)
y
En la figura 31 se muestra
oscilaciones caen exponencialm
Figura 31. Vibración libre d
subamortiguado
En la figura 31 las amplitud
periódica y son marcadas con
amplitud para n ciclos de osci
(6.13), como:
Xo
=
exp(-n8)
Donde 8 = 2rc s/(I-(~?)j'h es
corresponde a la relación entr
en la figura 31 para valores pe
1, el decremento logarítmico p
Usando la ecuación (6.14), se e
Xn
Xo
=
exp(-2rc ns) = 1
2rcs
Usando este prinCIpIO se mid
viscoso en un sistema. El sis
generando una velocidad inici
libre. Usando la ecuación (
puede ser evaluada. En la F
amplitudes de vibración libr
respecto a la relación de amort
0.20
o
~
(t\
0.15
ti
ro
::'
Of)
.~
t:
o
ti
ro
1])
-o >:: o
o
~
.~
ID
.P:::
O.OQ
0.1
O.Z
Figura 32. Variación de la r
amortiguamiento.
cl Sistema críticamente amort
característica dada por la ecua
negativas. Aquí el sistema no
solución es de la forma X = (A
La solución para las dos condic
El movimiento es mostrado e
tiempo la curva entra en reposo
d) Sistema sobrcamortiguado
amortiguamiento es mayor
distintas para la ecuación c
Donde: A = 1 ( X o + --".---"'--"~ l.., B
2\
(Un)
-1
En la Figura 30, se muestra el
sistemas estudiados.
Si la masa es suspendida p
muestra la Figura 33, el resort
respecto a la posición de equilib
/'
In
Figura 33. Modelo de un sistema d
deflexión estática debido al peso. En este caso la ecuación del movim
x
mi( + e + k (x + 0st)
mg
Desde que la fuerza en el resorte de
peso, esto es : kOst = W mg, la ecu
x
mi( + e + kx =
°
Esta ecuación es la misma ec
Con la ecuación (6.21) y con
natural puede ser obtenida po
Wn=(gj6stll/2
Un valor aproximado de la fre
sistema mecánico complejo p
grado de libertad. Por ejem
ruedas puede ser reducido a
juntando las masas de todos
rigidez equivalente del eje utili
2.2
Sistemas torsionalcs
Los ejes rotando transmitiend
torsionales si el torque no
cigüeñales de los motores. En
transmitido puede fluctuar
engranajes, o errores en el co
en vibraciones torsiona1es de l
Un sistema torsional de un g
34. Este tiene un eje de mas
amortiguador con coeficiente
mamen to polar de inercia J.
Figura 34.
libertad.
Representación d
La rigidez torsional es defini
unidad de ángulo y al coe
resistente del amortiguador
amortiguamiento puede ser
inherente a la estructura amo
sistema en torsión es dad por:
cJ8+c8+ k8
O
La solución de esta ecuaclO
(6.1), excepto que J reemplaz
y coeficiente de amortiguamie
2.3 Vibración Forzada
• Sistema excitado en la m
armónica Fosenwt actuand
35.
Figura 35. Fuerza oscilante F
La ecuación del movimiento e
mi + e x+ kx = Fosenwt solución particular es u
frecuencia w de la excitación.
ser escrita en la forma:
xs Xsen(wt -
el En donde x es la amplitu
desplazamiento con respecto
Sustituyendo en la ecuación (
(
Xs
F /\
jsen(wt-o)
Ik
Usando la parte complementa
solución completa sería:
Si el sistema es no amortiguad
c = O en la ecuación (6.28). C
frecuencia de excitación coinc
üJ/üJ n = 1.0, la respuesta del si
amortiguado, la parte co
exponencialmente y podría se
de oscilación. Las expresion
obtenida de la ecuación (6.27)
-~7
Fo/
/k
/
r
~- ~)
[ \ w,
1
)
(
J
+I
/
\
.
\2!~
2~(.:J I
W
n
)
y la fase entre la respuesta y l
8
=
tmyl
Cuando la frecuencia w c
amortiguamiento Wrl, la amplitu
x.
mnx
Foí
/k
1
= ___ ....... _--:-;­
~(4-J72l
:-,
La máxima respuesta o resona
Para estructuras con bajo am
igual (.)n, y la amplitud máxim
La ecuación (6.29) y (6.30) ind
.Y la fase O son funciones sola
del factor de amortiguación ?
Figura 36.
lQ
r.
.....o
ti
"'­
-'"
'"'
"'O
::J
~
c.:..
6
S
liS
1))
"73
¡::
4
o
<~
u
~
(1.1
pe;
í'
o~~~==
o
Relaclo
Figura 36. Relación entre l
ángulo de fase debido a una fu
Estas curvas muestran que
influencia sobre la amplitud
frecuencias próxima a resonan
La velocidad y la aceleración
amplitud con respecto al tiemp
x,
Velocidad: - - - ­
FoW¡{
'«
[
Aceleración:
, 1 (J2
12
/W
\
/
Fo(') ;/
/k
Las Figuras 37 y 38 mues
ecuaciones (6.34) y (6.35).
10
1;
"
B
<:;> ---'"
LL
)oC
6
oL-__
-L~
O
RelaclOn
Figura 37. Respuesta frecuenc
• Transmisibilidad. La fuerz
sometido a una excitación
FT = C X + kx
Sustituyendo la respuesta d
ecuación (6.36), se obtiene:
lO
....b'"
--...
S
,lo<
¡:¡
o
u
~
...
(I;l
6
.'!L)I:!
o
4;
ID
'"el
e
"
-o
rj
JI!
2
ID
O::
Relaci
Figura 38. Respuesta frecuenc
F¡ _
- - Tsen((,)t-O)
Fu
La magnitud adimensional de
(6.38) El ángulo de fase entre FT y Fo
e = tan!
1
La transmisibilidad T versus
la Figura 39.
10.0
9.0
8.0
¡...
7.0 "eS ro
"eS
~
6.0
::3
""E
¡::
""
...(­
(\'\
5,0
4JJ
3.0
".0
1.0
VelocId
Figura 39. Gráfica para la tra
Para bajas relaciones de fre
unidad, mostrando que la fue
la base. La transmisibilidad e
natural del sistema y para a
transmitida decrece considera
entre la fuerza transmitida y l
40.
:wo
180
160
v,
Lo' w
'"L.,
....,
140
o 120
.,.
'D
,1
,il &.. 100
80
(tl
"13
60
40
20
o
D
Velocidad
Figura 40. Angulo de fase entr
• Desbalance rotatorio.
C
rotatorio son montadas s
fuente común de excitació
sistema coincide con la
desbalanceada, resultan s
estructura de soporte. En
de masa M, cuyo desbalan
excentricidad e que rota a
desplazamiento de la masa
de la masa m relativo a la
movimiento es entonces:
Figura 41. Sistema dinámico
(M - m)x +m(x + X rn) + eX + kx
El desplazamiento de m relativ
X m ==
esenwt
(6.41) en (6.40):
Mx + e x + kx == me(,)2 sel1w t Esta ecuación es similar a la
por mec,J 2.
solución es si
adimensional quedaría:
sen(cat-8)
x M
e m
y el ángulo de fase: TanO
==
La solución completa quedaría
x
exp~ sc0"l { ACXP[(S2 ~ l)Yi (o'" J
me
sen(Ú)t··O)
+
Im(
1- 1,"
,
Ce) n
+eSI¡I
/ CJ n
r
• Movimiento del soporte. Cu
como lo muestra la Figura 4
u(t]=
Figura 42. Sistema excitado e
la ecuación del movimiento pu
mx + c(
x - u)
+ k(x
u) = O
Esta ecuación puede ser escr
mx + ex + kx
Donde: Fo
cUo (¡)COS(¡)t + ku
UO
(k2 + C2b)2)
y
La solución de la ecuación (6.
por el ángulo de fase (p.
• Resonancia, sistema de
vibrando se dice que entr
máxima. Las respuestas
máximas cuando (¡) (')n (1
Mientras la respuesta a la vel
En el caso de un sistema n
cuando b)
(,)n, siendo ú)n la
Para
un
sistema
amor
amortiguamiento es dada por:
En muchos sistemas mecán
frecuencia de resonancia y
pueden considerarse aproxim
Cuando el sistema desprec
frecuencia tiene un agud
amortiguamiento es grande
grande como se muestra en
un valor específico de amortig
El factor Q es definido como:
Q = 1/2C,
Rmáx Esto equivale a la respuest
amortiguamiento. La banda
curva de respuesta medida
respuesta es Rmáx
. Para
puede calcularse aproximadam
____ ~~,!C_
~
'-'
Il¡
'V
:J
R
~/
·lnaA
-.-...-----.. . . . --~
o..
tl1
'.v
O:::;
Figura 43. Reson
• Sistemas torsionales con
de la Figura 34, si el
sinosoidal, la ecuación del
Esta ecuación tiene la mism
puede ser obtenida reempla
coeficientes de rigidez tor810
respectivamente.
3. SISTEMA CON VARIOS G
El sistema de modelo de
suficientemente el comporta
información sobre altas frecu
modelarlo como un sistema
analizar un sistema de vario
sistema de dos grados de li
estudio del comportamiento d
3.1 Sistema con dos grados d
• Vibración libre. El sistem
dos masas mI y m2, con c
de amortiguamiento Cl y C
Figura 44. Sistema de dos gr
Las ecuaciones del movimien
Asumiendo una solución de
(6.57)
(6.57) en (6.56):
De las ecuaciones (6.58) se o
La ecuación (6.59) representa
raíces; siendo la solución co
determinadas con las cuatro
• Vibración forzada. Cuan
resorte es sumado a un s
del principal, el sistema s
sistema principal y sol
actuando sobre la masa p
las ecuaciones del movimi
Asumiendo una solución del
(6.61) en (6.60), se encuentran
D2((V~- (1)2)J
-
A1
OJ¡2[2D¡(V¿;2(1J 2 ")"}
-
D~ -1-
_ O)¡2 [D¡
A2-
((V~ - (j) -1- 2D 2 (O¿;2(r)2
1
O;
D¡? -1-
3 -
A4­
J
7
D;
-1­
(O¡2 (2!)¡ W~-2(Vl _
A -
D:; J)2{()~)
D~
W¡'(!)¡(lJ; +2D2 (I)¿;2(¡)2)
1)2 -1- l)2
¡
2
Donde:
_k/rr .
Cl)2
1 -
k
l
.{
m ' W2 -- /rr2
. m
'~l
1
_c~
-
2
Las respuestas también puede
Donde:
Bl~(AJ-I-A~)Y~
2
Y B·:2 = (A3
-1-
A2
.1
3.2 Sistemas con varios grado
necesario conocer los varios m
respuesta de la vibración. Cu
puede ser modelado como u
libertad, concentrando su masa
de sitios o estaciones sobre la es
El número de grados de liberta
coordenadas independientes q
movimiento o la configuración d
amortecida, si el movimiento es
número de grados de libertad
movimiento es en el plano, el nú
dos veces el número de masas a
• Método de Holzer. Cuando
consistente de varios disc
libremente en una de sus fr
una fuerza, momento o torq
En el método de Holzer, est
frecuencias naturales y mod
Figura 45, muestra un
conectados por ejes.
Figura 45. Sistema torsiona1 co
Holzer propuso un método de
empezando con una amplitud
calculando progresivamente el t
otro extremo. Las frecuencias
condiciones de borde compa
frecuencias naturales del sist
cualquier sistema de paráme
masa-resorte, vigas resorte, etc.
Para una frecuencia w y 81 =
primer disco en la Figura 45 es:
Este torque es transmitido al dis
El torque inicial del segundo d
inercial del disco 1 y elíseo 2 es
la cual da:
Continuando con este proceso
inercial combinado de todos lo
extremo mas alejado:
11
T
I.fío/Oí
Donde n es el número total de
el torque tot.al T podría desapa
valores de Gl, las frecuencias na
MODELO 1. Una rueda de aut
una barra de acero de 0,50 cm
muestra en la Figura. Cuando
angular y se la suelta, realiza 1
momenlo polar de inercia de la
U
La ecuación de movimiento cor
JO = kO, en donde J es mom
rotacional y O el ángulo de rot
de oscilación es:
10
(¡)n
2n ---30,2
2,08
La rigidez torsional de la barra
donde Ir nd 4 /32 es el mo
transversal de la barra, f = long
1 =~(O
p
32 '
10- 2 )4
(0,00
(80)( 10'1)(0,006136
k
2
Sustituyendo en la ecuación de
cJ == k 2,455
2,08
=
°' 5
MODELO 2. Los datos sigu
vibratorio con <lmortiguamiento
c = 0,12 lbjpulg por segundo.
razón de dos amplitudes suces
La frecuencia no <lmortiguada
. _ .~8()~;
.
fk
m"
1
fII
El coeficiente de amortigu
amortiguamiento C; son:
Ce
=:
2m(l)n == 2
e
X
10 X 34,0
386 0,12 _ 0,0681 1,76 e(
El decremento logarítmico
brCO, ()(íl) 1)
Jl=O,0681
2
0,429
La razón de la amplitud de dos
=
C()A2'¡
= 1,54
MODELO 3. Una máquina d
resortes con rigidez total de 70
balanceado que se traduce en
velocidad de 3.000 rpm. Supo
C;
0,20, determine (a) su
desbalance, (b) la trasmisibilid
La deflexión estática del sistem
100(9,8
700x(10')
1,401 mm
La frecuencia natural sería:
/"
1 r--9$t
2n ~ 1.401(10')
'=
13,32 Hz
(a) La amplitud de la vibración
350
x = ---r===========
l
2(O,2
=0,0379 mm
(b) La transmisibilidad de la e
(
-'- I 2(0.20)
\
.
SO
.
13,32
T=-c==~==~========
(e)
La fuerza transmitida serí
MODEL,o 4. Si las masas y
Figura son iguales a m y k res
2
(,J]
k
= --­
nl
Determine la vibración libr
iniciales son:
Xl (O) 5
Xl (O) = O
PX
Cualquier vibración libre pue
sus modos normales. Así, los
como:
Los pnmeros términos de la
normal a la frecuencia COJ. SU
=A/A== 1, que es la primera form
razón de amplitudes Bl/B2 ==
modo normal de vibración. Las
libertad de desplazar el origen
modos normales. Las constan
condiciones iniciales, que pued
Haciendo t = O Y Xl (O) == 5, X2 (O
5 A se
O == A se
Reagru pand o:
A sen
\1/
B sen
'1
Diferenciando las ecuaciones
haciendo t O, se obtiene:
O = OllA
lA
O
(1)
cm;
\111
Por lo tanto:
COS\I'2
La solución es entonces:
Xl = 2,5 cos
X2 == 2,5 cos
Que en [arma matricial:
{\,~
= 2,5
CI} c
PROBLEMAS
1. Una masa mI cuelga de un
tico. Una segunda masa m2
rebote, corno muestra la F
guiente.
2. Determine la rigidez rotacio
su período natural.
3. Un motor eléctrico de 68
aislante de 1.200 kg y, la
de 160 cpm, con un factor
desbalance en el motor q
determine la amplitud
trasmitida al piso.
4. Escriba las ecuaciones d
en
la Figura y determ
modales.
m¡;m ~k
~
5. Determine las frecuencias
sistema mostrado en la Figu
3,86 lb
gm2 == 1,93 lb
gml
Cuando se excita con FI == Fo s
amplitudes y grafíquelas contra
CAPITULO VII. T
1. INTRODUCCIÓN
Los engranajes son órganos
potencia o movimiento entre d
poca vibración, mediante el e
ruedas dentadns. La combinac
misma transmisión se conoce co
El empleo de trenes de engranaj
través no de un par de ruedas
muchas ocasiones, sobre todo e
transporte. Tres casos típicos s
a) Cuando la relación de trans
transmisión elemental o dir
puede resolverse con un tren
b) Cuando la distancia entre
demasiado elevada para una
e) Cuando dicha relación de tr
gran número de cifras en
inconmensurable.
Según la posición de los árboles
.
.
} Engranaj
>- Arboles paralelos Engranaje
Cremaller
~
'y
Árboles que se interceptat E
Árboles que se cruzan
Eng
Rue
} En
En la Figura 46 se presentan lo
Tabla 6 1 sus aplicaciones, ve
Engrane ext.erno
i
I
(
I
Cilíndricos de dientes rectos
Engranajes de tornillo sinfín
i:;;ngranajcs cónicos
Figura 46. Tipos de engra
Tabla 6- 1 Car
-
...
_- __ _-...
...
TIPO
Recto r:xterior Recto Interior
Helicoirlal Espina pescado (Herringbone) ..
~---~-------
-----
APLICACIONES
r:::jes pan1lt-~los
Velocidadcs moderad
- [~jcs paraje los
- Velocidades moclcrac
Igual sentido c!e rotac
Ejes paralelos
Velocidades alias
E.les pamlelos
Velocidades altas
- Servicio pesado
En los engranajes internos, la
es positiva e inversamente prop
externos la relación de velocid
inversamente proporcional a lo
La relación de velocidades de
proporcional al número de d
diámetro de paso. Las ecuaC
simple son:
.
, n
Donde n se da en revolucione
Estas ecuaciones pueden ca
velocidad entre el primero y el ú
En la figura 47 (a), se presenta
hay solamente un engranaje
muestra un tren de engrana
engranajes pueden rotar alrede
Figura 47. a) Tren de engranaje
Se nota que el número de dien
engranes impulsores y el núm
engranajes impulsados. Los en
impulsados. Cuando esto suc
este engranaje se cancelará c
engranaje se conoce como engr
que el número de dientes se
afectan la magnitud de la rela
cambian las direcciones de ro
las figuras. Los engranajes in
ahorro de espacio y de dinero.
en la figura 47 se presenta repe
de engranajes con la misma di
2y
teniendo la misma relaci
Figura 48.
(2,3,4 y 5)
Los engranajes 2'
La ecuación (7.2), pueden ser s
Donde el sIgno menos es
engranajes giran en sentido con
En general, la formula de la
engranajes será:
n último
de los núm
-"---.-----.----.
n primero
productos de los núm
En el tren de engranajes comp
velocidades para los pares de e
n,
N
2
Nnz
.1
y
N
n, -
N
n4 por estar en el mismo c
encuentra:
113 =
Lo importante aquí que se debe
todos los engranajes constituye
son requeridos para determina
sistema.
Los trenes de engr
sobre los trenes de engranajes
velocidad sea grande. Por ejem
el engranq¡c final cn un tren
primer engranaje.
2. SELECCI()N DEL TIPO DE E
La disposición de los ejes que v
generalmente sugiere el tipo d
paralelos o se interceptan o se
tipo de engranaje más indicado
3
Figura 49. Tren de engranajes
Varios tipos de engranajes.
helicoidales paralelos, que tiene
n:=
J
N n2
.1
Los engranajes 4 y 5, engr
velocidad:
Los engranajes 6 y 7, tornill
ligeramente de una manera dif
tres o más filetes. Con un file
de rosca del filete, con dos filel
paso de rosca, así:
n7
Número de filetes del sin
:=
N7
Reuniendo las ecuaciones (7.7)
Donde N6 = número de filet
engranaje 7 es mostrada en l
asignada al tornillo sinfín.
3. DISEÑO DE LOS TRENES D
Un aspecto importante al def
número de pares necesarios y
satisfacer una cierta relación d
i== (¡) inicial! (¡) final
Como norma general se tiene
par de engranajes que compon
número máximo de dientes n
presentar los siguientes casos:
a) La relación a conseguir
inmediata con una sola pa
por lo tanto se utilizaría u
ellos tuviese 100 dientes y
b) La relación esperada es m
solo par es necesario utiliz
superior a 127.
Por ej
conseguirlo con un solo
engranaje NI 693 dientes
dientes NI = 693 excesivo.
dientes en factores más
parejas de engranajes:
. 693 21 33
1=
100 10'10
Se utilizaría dos parejas de eng
la segunda con N3 33 Y N4 =
Si el número de dientes es sup
en factores hay que utilizar el
reducidas, pues resulta im
deseables de funcionamiento.
El método se basa en ir separa
La parte decimal se expresa e
unidad volviendo a descompon
decimal.
Si en cada desco
denominador, se obtiene para
exactas a la relación deseada.
Por ejemplo con i
6.55
==
655 _
100
=
Se procede de la siguiente mane
Primera aproximación:
i
==
6.55
6 + 0.55
=
==
6 + 55 =6
100
Si se elimina la parte decim
i=7 =70/10 Segunda aproximación:
1
Í=6+
_
=6-
1+ 45
55 Si se elimina la parte decimal
una relación i
13
2
6.5
=
65
JO
- Tercera aproximación:
1
1
i~.=6+---
11
10
6 + - - - - = 6 + --1+
1+--
45
1
1+
1+ -45
10
Si se elimina la parte decimal d
una relación i = 59
9
cl =
6.555, que e
En el caso que se requieran
7, se pueden aplicar los cas
en la descomposición resu
dientes se multiplique num
fije el número de dientes e
Si i=217,entonces:
i = 31 (7)
JI(2) 7(10) 6(15)
--. -_
. .­
10 2(6)
15
Se resuelve con tres parejas
transmisión de cada par es me
d) Si la relación de transmisi
irracional, necesariamente
4. TRENES DE ENGRANAJES
En las secciones anteriores se
tienen sus ejes paralelos y fijos
de uno o más de los engra
permanecen paralelos, se pres
conocida como trenes de e
mantienen unidos por un braz
Los engranajes planetarios o
dentadas cilindricas o cónicas
que pueden girar alrededor d
engranaje sol gracias a que su
portador o puente (Figura 50)
Figura 50. Tren de engranajes
Para analizar las relaciones de
dichos engranes planetarios, s
de engranajes, ecuaClOn (7.4).
implica analizar el tren dc eng
el espacio. Así, se estaría vien
con respecto al portador de
observador imagine que alguno
fijos, sean capaces de girar. D
se comporta como un tren d
portador de planetas, la fórmu
como:
n último relativo al brazo
Trene=
n primero relativo al brazo
Donde: nF rpm del primer eng
nL == rpm del último eng
nA = rpm del brazo
Aquí nuevamente el tren e se c
Tren e
=
Producto de los números d
Producto de los números d
Se a.sigl1a lln signo "+ o
dependiendo de si el último en
sentido o en sentido opuesto qu
Los trenes de engranes planet
para aplicaciones que requiere
reducción de velocidad y que
poseer mayor número de dien
grandes esfuerzos.
Si se desprecia la fricción en
entrada y salida del tren deben
TúItltTIU
nultímo
Tprím
Esta ecuación (7.12) proporci
salida de un tren de engranaje
Los engranajes planetarios o ep
• Trenes simples o de un pue
engranadas entre si o a tr
con un puente alineado con
muestran en la figura 51.
p
s
P,
P,
s
I­
( ("
~~­
Figura 51. Trenes planeta
• Trenes compuestos o de va
simples genera el tren com
indica directamente el núme
indica la forma como se gene
1REN A __
Figura 52. Trenes planetarios c
Los trenes de engranajes
inusuales porque tienen dos
movimiento restringido debe
permite actuar como mecanism
dos velocidades de giro indepen
tanto, el número de grados d
igual a (2 x número de trenes
número de grados de liberta
ligaduras entre los engranajes,
para cada conjunto, lo que
apropiada caja de velocidade
simple que tiene dos grados de
de transmisión, mientras que
unidos proporciona inieialmen
permitirían fácilmente hasta 15
5, TREN DE ENGRANAJES DIF
Se trata de un tren epicicloida
concurrentes, es decir lo que
utiliza en máquinas donde el m
un eje primario a semiejes sec
misma velocidad pero pued
conformidad con las reacciones
Los diferenciales más comune
y los más sencillos se compon
solidaria con la caja de satélite
unidos a la caja y otros dos uni
El mecanismo diferencial es re
caja aetúa de puente movien
como planetarios que son los q
engranajes cónicos que actúan
El diferencial sencillo correspo
exterior, en donde los satélite
ejes perpendiculares, como lo m
Corona
Figura 53. Tren diferencial sim
Como rl
0=
r2, se encuentra:
2
Cuando nI == n;1, entonces nI
semiejes es igual a la del chasi
pueden ser distintas sin que se
tanto, la del piñón que lo accion
clásica en los ejes traseros de los
lo que se llama el grupo diferenc
traseras puedan girar a la mi
necesidades de transitar en recta
Los diferenciales dobles utilizado
su caja doble número de satélites
MODELO l.
En la figura 50, el engrane Sol e
de las manecillas del reloj a 100
estacionario por estar sujeto al ba
rotación del brazo.
Sea nF
0=
n2
==
100 rpm y n1., ==
115 =
Liberando el engranaje 5 y mante
Tren e
·0.25
En la ecuación (7.11):
nA
0=
0.25
==
_~
(-
20 rpm
La velocidad angular del engrane
a:
1123
= 112
- 113
La velocidad del engrane 4 relativ
n 43 == -~
Por lo tan to:
11 2.1
20
30
Pero
11
2
Sustituyendo los valores, se obt
-
2
3
==
­
=> n'l =33.33 r
(-100)-(-20)
MODELO 2.
La figura muestra un tren pl
movido por su eje y a 250 rpm.
5 son planetarios articulados
transportado por el brazo plane
rotación del brazo. El engranaje
34dre
Para este tipo de problemas, d
como primer y último engranje
los engranajes 2 y 6 son dadas,
ser utilizado como el primero.
escogido el engranaje, no puede
Escojamos como primero el eng
Sabemos que:
E
~~EJ
n[
nL: RP.M. del último engranaj
nr: RP.m del primer engranaje
nA: RP.m del brazo
También
E = Producto del nú
Producto del nú
n( = n2
n!.., = n6
= -250 RPM
= O (estac
E=~){N'i = 20x16
N 4 xN 6 30x34
Entonces tenemos que:
16
51
=
E
Reemplazando por sus equival
16
51
(-250 RPM - nA)1
16 x 250 RPM
=
(
16x250
nA= - - - 11
nA
114 RPM
PROBLEMAS
1. Hallar la velocidad y direcci
valor del tren E? n8?
1200
•
3 3d
2. Los números de dientes de
son: N2 = 20 N3 = 18, Ns
estacionario. El brazo 4
engrane 2 es impulsado a 330
Determínense la velocidad y el s
3. Los números de dientes de los
de automóvil ilustrado en la fig
== 16 N6 == 16. El eje principal de
será la velocidad de la rueda de
gato en este lado y la rueda izq
superficie del camino?
4. Un automóvil que utiliza el d
vuelta o vira a la derecha a una
24 m de radio. Considérense lo
el problema 14-23. Las llanta
diámetro, y se tiene una distan
de rodada o distancia entre rue
a) Calcúlese la velocidad de cada ru
b) ¿Cuál será la velocidad del engra
A rueda , - - - -..1
trasera " - - - - - { I
CAPITULO VIII. CAL
1. CORREAS O BANDAS DE
1.1 Introducción
Entre los medios de transmi
constituyen un sistema de
que las hacen recomendab
industriales. Las correas se
entre dos ejes paralelos o c
necesita mantener una relaci
En la mayor parte de las
potencia debida a desligami
ciento.
Sus principales ventajas son:
Funcionamiento silencioso
Absorben bien los efectos
funcionamiento irregular
máquiGa receptora. No requiere lubricación, p
Facilidad de instalación Facilidad de adoptar dista
Se puede transmitir desde
consideración. Pueden ser utilizadas para
ejes que se cruzan y a ejes
Buena adaptabilidad a la a
Se puede emplear hasta p
casos especiales superar e
Si la selección de la corr
alcanzar una eficiencia del
Inconvenientes de las correas
o Implica mayores dimensio
o Puede producirse resbalam
correas planas.
o Debido al tensionamiento
o Sufren variaciones por efe
o Con el trabajo sufren a
potencia disminuiría consi
o El coeficiente de fricción s
otros factores.
o En algunos casos es impos
El diseño de una correa im
(material, longitud, sección
potencia en ciertas condicion
Los cálculos de las correas
cuenta todos los efectos que
una correa es dinámica y pos
>­
,.,
':Y
Está continuamente te
poleas. Debido a esto,
cometiéndose cada secc
El resbalamiento produ
desgaste.
Absorbe las vibraciones
Para
cálculo de las corr
métodos simplificados.
Ac
información en ábacos y t
detallando claramente sus ca
Los elementos altamente flex
se utilizan es necesario esta
prevenir el desgaste, el envej
elementos deben reemplazars
1.2.
Clasificación
Las correas se pueden cla
disposición del montaje y la m
el empalme.
a)
Según la sección transve
• Correas redondas:
relativamente liviana
también hay correas
equipos agrícolas. S
entre 1/8 y 3/4 de
funcionamiento requ
tam bién como roldad
• Correas planas: req
poleas abombadas.
transmisión donde
distancia y la posici
pequeñas variaciones
a 0.20 pulgadas).
molinos, aventadoras,
• Correas trapezoidales
con garganta y son a
de cuña de la correa
conlleva a un amarre
fuerza de presión n
dimensiones de la se
trapeciales) han sido
cada sección designad
para tamaños con dim
las dimensiones, diam
potencia para cada un
TABLA 8.1 Secciones de ban
N~CHOa.
;n
el",
ID
A4ii;~
A
B
-H
e
D
!:
E
11
Para especificar una banda e
la banda, seguida por la circu
Una banda C85, es una
circunferencia interna de 85 p
Tabla 8.2. Circunferencias in
A
26,31. 33, 35,38,
75, 7H. 80. 8S, 90.
B
35. 38.42,46.48.
79,81,83,85,90,9
144, 15R. 173. 180.
e
SI, 60. 68, 75, 81,
IT\ 180. 195,210
D
120, 121!, 144, 158.
390. 420. 480, 540.
E
I~O,
.•
•
_
195,210,240
Correas en V con ban
sido vulcanizadas pe
Funciona como un co
los problemas que pu
elevadas potencias co
contra la otra.
•
•
•
Correas en V apostillada
dientes de sierra. Al ig
dependen de la fric
Comparada con las a
aumento de la superficie
Correas reguladoras, d
correas planas con dien
ranuras axiales formada
las poleas con llanta est
o desliza y en consecu
relación de velocidad a
polea debe estar alinead
la correa se colocan ca
entrelazados en forma
tensión y mejorar su res
Correas eslabonadas: es
el ensamble y permite
recomendables para alta
b) Según la disposición del mo
•
•
Transmisión abierta (dir
en el mismo sentido. En
plana la tensión en la m
colgadura cuando la ban
Transmisión cruzada o i
opuesto. Las caras o lad
poleas, de modo que esta
con correas en V o de sin
c) Según la manera como se
carriles tensores mediante
o pivotando ligeramente la b
d) Según el material
• Correas de cuero (su uso e
• Correas de caucho, re
vegetales o metálicos qu
tensión.
• Correas de textiles
• Correas plásticas
• Correas tipo cintas metálic
e) Según el empalme
Se encuentran correas engr
enterizas o sin fin que son
uniforme
1.3.
Cálculo de transmisión
- Datos Necesarios para el cá
P:
N
N:
Potencia a transm
RPM de la polea m
RPM de la polea m
Además, las co
máquina acciona
y puntas de carg
de funcionamient
torsión de régime
Relación de transmisión (k
Potencia nominal o correg
que señala el fabricante
carga constante, pero en
necesario corregir la pote
tenga en cuenta las condic
Potencia corregida
o proyectada
TABLA 8.3 Factores de servic
fu
Normal
Pesado
de 6
1
en march
Punta ele carga o puesta
trabajo a plena carga
se
Sección de la banda
Redetermina como una fu
de giro establecido, median
400J
,-,
7­
30C"':
V
X
201){)
O
z
~
<~
uJ iOOG
,.J
O
el
:¿"
c.:
-,
i.iJ
O
O
a:
~{)ü
1CD
3Cu
LJ
~
::>
z
:t'JO
lOO
POTENCIA CORR
Elección de los diámetr
El diámetro primitivo
con la tabla 8.4, que
función del ángulo [3 d
los diámetros primitivo
Tabla 8.4 Diámetros primiti
gargantas. (Para polea menor)
:;,3
de
a
de 50
de 75
pEtra diámetros pnrnitivos lulcrlores
Para estas tr"anSmlS10!!CS de Car[1cter excepc
r--:ota:
Tabla 8.5 Diámetro primitiv
A
sn --­
80
53 ~
85
50 +
YO
56
6J
67
f· ;
71
++
17
18
'GS
80
IIB ;. +
19
; ·1
20
22
+
I
f.
loO
1011
11(
~o
\
95 75
10t]
¡.
1-'1
14
ISO
-¿.J
+­
28
JO
lI'¿
¡:¡S
141)
1SO
1&~j
~
+
,"/0 .
JI
35
1se
160
180 +­
200
22,1 -+
2~O
,
190 ­
~o
200 ..
(lj
n~
50
53
¿:iO
~. -~-
+ \
37
'2J3J
55
315­
6.1
:JS5 i
7\
::O'J
.f
~oo
~
75
r.O
90
s~o
+
t­
+
G30
EGO
IDO
112
~
\000 -4-
+
no reco:nend3dos
+
++
recOmerd3d03
esoeclalmente recomendados
El diámetro primitivo de la p
D
k-d
Si D estuviera ya fijado: d ==
Distancia entre ejes (I):
establecida previamente por
con el siguiente criterio:
Para 1 ::; k
Para k
2:
3
3
Longitud primitive de la co
calcula:
(D d)
2l + 1.57 (D +d) + -'---4l
L
Con este valor L se calculado
mismo.
Si L';t. L se variará la distanc
disminuyendo o aumentando
La distancia entre ejes correg
re
L - L'
l±-2
Determinación del arco de co
sobre la polea menor se pued
O-d
lc
Potencia transmisible por co
base Pb, es la potencia en H
hipotéticas de trabajo a saber
e 180
a) k
=
1 ,O
57.
d y t)
180
b) Longitud primitiva estand
marca Pirelli; A68 - 890
Por las tablas de prestacion
correas Oleostatic Pirelli a p
primitivo de la polea menor s
está indicada este tipo de cor
Algunos fabricantes especifi
diferencia Pd por el hecho de
valores de Pb = fiN, d) y de Pd
Otros fabricantes en la pot
adicional (en el d equivalente
d se obtiene el d equival
equivalentes).
La p restación real Pa para co
Pa
=
(Pb + Pd). CI) . CL Donde: C n : factor de corr
eL : factor de co
tipo de banda (Tabla 8.8)
Tabla 8.7. Factores de correc
180
0
•
'!lO
I!"
I'l()"
lGS" leo
0.75 0<16 0.17 0.19 0,80
Tabla 8.8 Factores de correcc
15
24
Z8
.35
42
48
z
0,80 O.8J 0.86 (l,92 0.95 0..96
A
0.82 O.SI
8
0,81
53
1.00
O.!X)
0.9) 095
0,85
(},88
e
,;¿¡
\,0
o,S>O 0.94
080 0,84
o
E
F
La velocidad tangencial de la
v
n.
N
d
60 1000
v =Q
La fuerza que transmite la
entre la potencia de diseilo y
Determinación del número de
entre la potencia corregida y
loa coeficientes de minoración
Cuyo valor debe aproxima
superior, para el número requ
2. TRANSMISION DE POTEN
2.1. Introducción
Al igual que las correas, la
transmitir potencia entre eje
tiene como ventajas importa
temperaturas más altas que
grandes o pequeilas entre ce
para accionar más de una
bien alineados, especialmen
cadenas anchas.
Las tra
seleccionadas e instaladas,
mantenimiento.
Si la ca
rendimiento mecánico es mu
2.2.
Velocidad de la cade
engranaje, su acción puede
mueve sin resbalamiento co
motor, o engranaje, rota unif
la cadena varía desde un v
continua en la figura 54 (a
muestra con la línea punt
velocidad de la cadena,
uniformemente a menos qu
que
engranaje motriz. Me
engranaje, se reducirá la var
....
"r:/. ­ -----0­
Figura 54.
Variación de la velocidad de la
cadena para un engranaje de 4
dientes rotando uniformemente.
Para un engranaje con 11
cadena es de un 47(% para u
dientes es menor de 1%. A
engranaje menor es 17 o p
debería operar uniformement
La velocidad promedio de la
conducida por el engranaje e
V
Donde: P.T.N
12
V= velocida
paso de
P
T
número
N= velocida
Aunque existe una tendenci
cadena para aplicaciones ordi
orden de 2500 pies/mino (1
pies/mino (20.3 mis) para ca
han sido operadas satisfactor
La relación de velocidad para
debe ser mayor que 10: 1. S
usarse dos transmisiones en
eje intermedio y otra desde
U sualmente es deseable usar
cadena, para prevenir la vibra
demasiado pequeií.os puede
inicial.
Como una ayuda para selecci
con buenos resultados, la sigu
(900
PC;í
~
Donde: P
N=
I
N )
pas
vel
2.3. Número de dientes del
deseable depende de varias
55, el ángulo a través del cu
engrana con el piií.ón, es igua
del mismo. Así, con un nú
rotación será grande y el de
consideración requiere un mí
para obtener una carga unif
paso particular de cadena, el
la velocidad de la cadena aum
nifica que la carga sobre la c
potencia dada, será menor c
puede usarse una cadena má
para la velocidad de la caden
diftcultades de lubricación.
Figura 55. Engranaje de la ca
La discusi6n anterior indiea
es deseable un alto número
engranajes grandes, las limit
de lubricación, generalmente
dientes. De aquí, que el núm
compromiso. El número minim
varios tipos de cadenas.
Es usualmente preferible usar
que el desgaste se distribuya
particularmente deseable par
lubricadas. Al reemplazar u
número impar de dientes se o
mientras que un engranaje d
alternos con mayor desgaste q
Para determinar el diámetro
utilizarse la geometría de la fi
8
sen2
O
p/ /2 O'
/2
sen(8j2)
sen(180jT
2.4. Potencia de diseño: La
es usualmente delimitada por
articulaciones.' El desgaste p
debidas a variaciones de velo
equipo movido, o ambos. El
paso de la cadena y el esla
dientes, con lo cual, al gira
dinámicas sobre las articula
desgaste se aumenta y la vi
Para tener en cuenta. las car
la potencIa transmItIda debe
para obtener la potencia de d
Tabla
8.9 Factores de servicio
Tipo de Carga
Carga uniforme, condic. promedio
Imp'lcto moderado
Impacto fuerte
'"------­
2.5. Cadenas de bloque: e
para aplicaciones de transpor
el desgaste es rápido, deb
engranaje. (figura 56)
Figura 56. Cadena de bloques
2.6. Cadenas de Rodillos:
están fabricados en aleacione
fuertes y durable, y dan e
seleccionadas, instaladas y lu
Las cadenas de rodillos han s
tamaños.
La figura 57 mu
distancia lineal entre centros
inferior entre las placas de e
simples, dobles, triples y cuád
<-
An\. hú de lOr;]1l
¡
_l~c
Figura 57 parte de una cad
Las cadenas de rodillos se
la Tabla 8-10. En el nú
indica: el 5, cadena de bu
O, indica una cadena de p
dígitos de la izquierda indi
velocidad recomendada en
8.10, para diferentes núme
La ecuación (8.16) expr
recomendada para una
potencias nominales son
Dividiendo la HP / hilera,
diseño (la cual incluye fa
hileras de la cadena. Las
dos o más hileras, pero má
En la ecuación (8.16), el
presión de apoyo permisibl
desgaste en estos puntos.
ángulo de rotación de l
en el engranaje, afecta el
función de f), mientras la t
término ViAl.
HP /hilera
(1+2
p
V
T
N
O
Donde: paso de la c
velocidad ta
número de
RPM del en
180/T
1 - cosO
vers 8
Tabla 8,10 Máximas RPM re
rodillos.
- _...._-... ..-.-.. . --1---'--¡--
:~;, i
Cadena N 0,';;,1}
p:~o _. __...
l',
-:-
\
¡I
,
1-'1' ~.- 1-
/I\!, l
I
¡
Dientes
I
-~l-;-'--I;~':) 1~)12', 2Gt;I'I",-~;~: 1
15
il,!HiOi2,5~IO 1,¡¡n l l
i.'i ,5 10;:! , :)()O¡ 1 ,:-1I °12
JI; . 070;: ¡. [ 1 1 "I:IOI:
10' ['):30!:1 .121),1 ,:i 10(2
J ¡i
17
Ig
!~)
1
17 . 21J(II:U~ HIII ,1'20 ,'';:
17 ;,~)(J!,\, ~170i I , 7!Hl 2
!7 . K
1• l\ H)j I . H;í¡ ;1 ,1
12
l;¡
1,1
20
21
22
2 ',')
Z\
°1
In.:1 \01:1 ,G\I)I! . n:IO!:z
tui
I< ,
30
31)
10
,15
r. lO¡'
1
.
.!1 ! l~ ():lfl¡:\
¡
I,~ ,,'i~l)i 1. 1:)');'2,020;:\
iR. ;lli '!,' ,Z:~i 111 ,~,o¡:\
,7 . ,)~o.\ . ,,) ¡(lit, ,¡';(). '2
n, 82UI:; J;-j (.11' ' GOO!2
¡
50
b5
,S~H
)8. OSI li' .211,1 1,'¡
tl,:l
1
•
1
I
I
:
'
¡8, 2:\1\; I ,:;OUII ~ll(),:\
,IR, ' :C"I'll ,:lf.ifl,1 ,'l70¡:\
',
.,',
'"
,8.1 R: 11 \ , ,1. HJI.:! . O,l! U
8, r,:;() I •. , SI);'] , O',J(j )::
1R
'
1 "
I
I
5, ,),-,Oi:!" 1 ¡ n¡ 1 ,.;oO¡2
r
5
I
m~¡2 ,L20¡ 1, lSOI' j
___60_ _-L.4_,_fJ_2(J2.~:.01-'
Debe consultarse la informac
2.7. Cadenas de dientes inv
traslapados unidos mediant
mediante juntas de balancín
la carga sobre el pin o el bala
su longitud, prácticamente s
ello que puede usarse una
coneXlOn será tan flexible
acomodaran por si mismos a
los engranajes, y es poco com
de una cadena silenciosa no
cadena de rodillos, y se han
de O.30m de ancho.
Figura 58. Cadena silenciosa
Las cadenas de dientes inver
indica la Tabla 8.11. En el
silenciosa" y los dígitos indic
la máxima velocidad recome
pasos y números de diente
engranaje pequeño deberá te
La ecuación 8.17 dá la pote
silenciosas, en HP / pulg. de a
por la potencia de diseño par
rango de anchos de la ca
preferiblemente 2 p Y 6 p. L
los máximos anchos estándar
.
Hp/pulg de ancho 2
=
P
V
53
l'
1-
Donde la potencia es la mism
I
Cadena N o
I
"-1
Paso
I
cc',....
,-,,,,:1
I
I
r,-'
C)tA
'""~-,~~--
····-----i-~-·
--'-" -
I i"
7"
---'-' ....--·-1----'--- .. -..
i\ncho máx.
I
i
Kúmero de
clientes
·1, rtfllJ
[,.1)00
:1. rtll( t
In
2l
ü,OOO
:l • ;¡lln
2J
2."i
27
ti, [1(i0
4. (XJi)
ú,OOO
1,o(){)
(, , I JO'.)
,1.00U
,1,0(10
;n
(), D' 10
t\,O(IO
~~l~
f, ,[Ji 'o
17
G,ono
35
37
5.1)00
40
:1, '}{IO
15
f
!)(')
;; , 50il
·c non
'1,0(1)
l,O(\O
3,500
3 . .')00
<I.oca
a.ooo
:1,:'00
2.51 lfl
• '.II'Il." ,
En
ecuación 8.17, el prim
permisible en los pines, y el
centrífuga y también, el núm
cual es relativo
á
2.8.
Máximo taladro de
necesario determinar si el n
resultará en un engrana
perforación axial de el tama
base, puede usarse las relac
mínimo de dientes que pu
engranaje de perforación axi
Engranaje para cadena de ro
T min
= 4d +5
p
T min
4d
.._-+
P
Engranaje para cadena silen
T min
4d
P
-._.. + 6
2.9. Longitud de la cadena:
determinar la longitud aprox
L
+T)
.T¡
. _--+
2
+
P
Donde: L
Tl,
C
P
p(T ¡-Tj
--
39.
longitud de la
número de die
distancia entre
paso, pulg.
La longitud en eslabones de
que se quiera usar un es
eslabones es que el ajuste
unidades de un eslabón en lu
La distancia intereses para e
los diámetros de los engranaj
La experiencia ha mostrado q
oscila de 30 a 50 eslabone
equivalente a 30 eslabone
admisible.
Si se requiere una longitu
interejes o combinación de
ecuación siguiente:
L = --'---"- +
2
Donde, la notación es idénti
entre la línea de centros y
engranajes.
Sena
2.10. Ajuste para tensión d
para ajustar la distancia ent
de la cadena cuando el me
pequeña holgura en la cad
evitar que la cadena se d
necesario usar pequeños en
el tramo flojo de la cadena pa
2.11. Protección y Lubricació
deben cubrirse para sumin
polvo y suciedades a la cad
del operario. La carcaza deb
inspección y lubricación.
Excepto una muy baja velo
del aceite.
Una cadena de alta velocida
agitación excesiva que eleva
alta presión que puede produ
MODELO 1.
Para transmitir una potenc
explosión de 6 cilindros, con
del trabajo a plena carga y
situado a 400 mm se quie
sabemos que:
La relación de tran
diámetro mínim
- El coeficiente para
de servicio
Calcular:
1 Tipo de sección de
2- Diámetro de la pol
3- Longitud de las cor
4- Factores de correcc
Prestaciones base y
6 Número de correas
1)
Tipo de sección
El coeficiente para hallar
"Condiciones de trabajo
"Pesado" y que el motor
Asi se obtiene un coefici
Potencia corregida (CV)
Entrando en el gráfico "
valor
la potencia cor
tipo de sección. En este c
2)
Diámetro de las poleas
Diámetro menor: 125 mm
Diámetro mayor: 125.1.5
3)
Longitud de las correas:
La longitud aproximada
expreslOn:
L =rr. (R+r)
Donde:
L: longitud de
R : Radio de la
r : Radio de la
c: Distancia en
Sustituyendo para nues
L
1
n(187.5+1 \
2
Ángulos de contacto
a
\
arcos
y = 360 - a
4)
R-r \
i
e
,....
= .:. '"
ar co
j
=360 -171.04
Factores de corrección
A partir del ángulo de
coeficiente Cl) de la tabl
A partir de la longitud
corrección CL de la tab
(tabla 8.8)
5)
Prestaciones base y adic
De la tabla correspondie
1- A partir del régimen
del diámetro primitiv
base que resulta ser
2- A partir del régimen
transmisión (1.5) se
ser O.
CV (Tabla 8.
6)
Número de correas a ins
Por tanto, son necesaria
transmitir
la
potenci
fi1ncionamiento y tipo de
MODELO 2.
Selección de
Seleccionar una transmisió
inducción de 1150 rpm a un
contra una cabeza de 30 pie
la bomba.
eficiencia d
transmisión puede asumirse
el trabajo es de 24 horas/ día
•
Selección cadena de rodil
HP transmitida
330
Selección de un motor de 15
HP de diseño
Paso
p:s;
12.2*1.2 = 14
( <)00
( 900
\ N
'" 1150
P::; 0.8
De la tabla 8.10 asumir paso
Asumir 21 dientes en el engr
El diámetro del eje del motor
De la ecuación (8.18):
4d
T min==
_
+:::> == ----'-
p
Por consiguiente, asumir 21
del engranaje menor.
De la ecuación (8.13) la veloc
v
pTN
12
o
o~_o
___
o~~~~_o_o_~o~o~_~
_ _
==
12
El ángulo de rotación de esl
o
l8()O
T
ISO"
_')
-:::;- - =8.)' 2l vers O =: 1
cos f)
HP / hilera == p2
==
0.7)
O
(
'
l
1-0
r.r
l'
7
-
(1
00(151
~~
1
!\ 2"
.)
~,:
_)'
/
O.,563 *1((L">
OJ .
\
15.3HP
Numero de hileras
HP
HP
Usar 1 hilera de cadena
Diámetros de engranaje
Engr. Menor :
Engr. Mayor:
Mínima distancia entr
DI + D2
10.05+ 5
Longitud de la cadena
+
2
=:
p
21+42 + 2*16 + 0
2
0.75
_ ......_ -
3l.5
+
~
42
eslabones.
• Selección cadena silenc~
dientes asumido, el paso
que para la cadena de rod
HP/pulg.
v
I~-
42
1
0.75'" 1510
1
53
"
15.6
Ancho de cadena
14.6 = ()'.. 9
15.6
Los diámetros de engranaje
que para la cadena de rodillo
..
~
t.,..~,
,
....
~ ,
-
U
_.J
'("1
" ' - , .,
,
.,
.-
':..o
.,.
'::"J.
::::::.
O
~
OC""'"
r.
~
(...J
7'
....1
.'".
. . ._
. _
O
O
I~ •
.-"'!
........
,"1
....1(.o< •
~
v>
C'l
o
-
~,)(_
'
,:;:¡..
o
'.J
_
:::;:
...~
~~
h
.2...JU.-
-
r.
.~ '~, ~
S
z: ;:,
\':J,
(.)
~,::
~
l,­
V)
O
"'
...J
(j
Tabla 8 ,6 (conr!nu~ción),
Prc-:;tJdor.:es d:! [;tS Correas Tr:1pe r,;ilfe5 OlECS'f A íiG Pl;l!:l_L!
p~:::3rACíC:\' ['¡~S::
. .::
:>
¿:
~7
'-,
Citw~el:O'l jJ:'m1t,.,;J5 el'! 1,1 '.'(;~C;;S H '¡,;'IQt
2
;r !--~~---~-~----_."---------------_._".
!:)
es
9::
$5
OiJ
v;,j
ü~':J
012
0>:1
{):S1
ü.t1
f)(,S
n
O~i:í
O~9
(';7,~
a 6J
0'7
-
,;)0
OJO' 036
~oo
tiC\)
DJ2
eao
C J)
O~l
~C'J
105
)5
ü:n
~~c
i35
t~i~¡
¡:S
HS
~:S0
;:;~
~ES
2 tU
2 JI
StS')
'2
l,t¡
Z).J
1~·
225
2!;!
2'~9
2(,9
;: -ts
2:'2
25.1)
2
~9
'J.::z
'2 .: ¡
¡53
~.i2
:iS5
:'?J
J:n
3JS
JJ~{r
2,3, XI
Par) !JS t,.".~i"i··~jI~'tlt::¡; if'1diC;Cl:; en
:,;¡
DJr:.¿: ·:O'C·'!3I..'J éi .iC;'¡rl',t:,o::J'C el
'J:¡O
10
I',J
(.J')
<11j
;'"
"..:;( C.:)";
,nI ¡:rJ';r
~
_,
1"\
'''u
", ' ....
1"
••~
VI
'-"";¡'
'~¡
'-',
<,t
r_l
0('".>0
\<'1
O
.,
,"
,~
C>
,....
•.,.",...
"\.¡
I!"
_'O'
"l
'J
,..,
,.
-
.::,~
•.;) 1..
",,·h ",.
.~
~
_
r.
1"'t
~
>"-,
c;J
~>{"""::;>v<:,,,,_~"'::)-
.-, ,- .. '" ,o, ,,'
<­
"'
'~5
....
~
I
t
,,.,
~
.-.-..:.., '" ;;'/ '.>
",... ,.
~ )
C' ' •..., ," 'r
u
("~
r,
o
.~-)
")
".f
"
.. .
.,
'1"'
_1
o o <.. -=.,
1~
r \
lit
r_")
.::,,<
'--4
~
-.
{'"";
I~
~
;..
b
,:)
C,
",.- ,;'?
'" '"
~t
"_
in V'I
~!1 t.l
{,)
"-Q
.'t
....... .,., t;'l
r'< ,-,
u
:::'~~OOOOQ
¡:::
.:¡
,n
1-­
O
W
_J
CJ
'.'
,,,
,r
','
";t;
;~
él
U
·f U~
'"
~
."
Ó
'o
.,v
'"w
'c:"'
e
(>
~
l,;'"i~',
A';}~
j!)d
./1
~,
,"') a
'.:..-
C)
0{
<:~
('<,
.. ,
(l
-
)o,
~
~
'J)
Q
\::!
r·,
........,
l,:.I-
;:
Tabla S ,6
rC,;~nUn!JaCión),
1fI ~,t~:
.0
-.(",
8 ' ...
¡..
t'
07"
-
Prcslo{:roncs
d~ r~5
Correas
Trí!,'lcc1clh'~:
r;~{r~L!
Ol [0514 ''(!C
------.._-..--------_
: : :' : : : : : :::~.,;:~1~~~~~?:~:,~~;:";-:~
----~-_.
o.
J
elJ
,r)
~I
1107
"
_
.}"
,;........
.~ 11 b· oJ~:;:'....:
'G.'" 1~~9·';:-~~
~~~~~,'.~~/;"
.. ,¡
. ; ' - ' , , < . . , .. . . . - J . . . . .
r;,
J
.r.')
~c
I~"J
·'1 ""'
'; ',~ l,"..,.... ~./",~
,.", 1". ,;:....
,_,
','
Á
...
- ..
1',
)">
lo
_'_'_-_-_'F
::¡1 1m ¡~¡:¡~:~ ji :¡ ~:j¡~ :lfJ:~ ~\ ~~;~ ~i~1 :¡ ;¡ i; ¡~ ~; ¡' ,,':C'¡¡; ~:: ¡¡ ¡r:¡];¡
l't~(~~118j~9!~tt;','
l '
al'
i~':':ü!~C'S
¡JCO Il t3 lAJl
,.~ ''-39
I~.c'}
,~7~ ,----::-------.....
~ll í'J:'lr2~~-ru 223~ ~
17 1d !C
1-"11$ lS"79 l111J 1~j:1 li?-::::~
,--- - - ,
23
1°
21 J.:
2j~~~ '),~ 2::!O,;~~ ~)':)
',l.-.-'
,--'
--~-
'l}';0 .'361 "11.?c. 7j,?r':.S.S~:."J-(..3l)'.. JZ::a~·~ lJj':
---~ .. ...
. '
951 H'.} 12.7~ 14=JI571IT.i~ \'11:; t:JTJ11U¡n~92J,4.jz.:~-BA2);..;:é'~72/&'rt~~~r¡I..tI:p21
"I::: ¡;~j~ 1~;¡i~ :¡j;,im ~t\,~?~J~:;;:~ ,,""~,~" ,U__
J
:
::j::t~E; '?-~;;~ '"
10
~
'JI
",-11' :~
:.'1""' "l'
" '.
i,l r',r;,~ :.
L:',"
,'1""'
iJ
u'", ('
-",':.1
:'~, ,:,
'0:"
1",
",',~, .-¡'
. (i . ~:.
• r1
r:'
'Tabla 8,6(co~tjn'Ja{.;f6f1)+- pr l.:staclones de hs CorreCiS Tr.:l;.'lé{,ij~c:;; Ol[O~;rtTIC rrRELU
,q:.j:ESTAC;(;:cv i::
~;..,13'1 ;.'J.
b
__
...
-,
e
~
J
Q:
~
z:
C.1¡ir!l!:~fO\
:¡;
_"'.
- '20
--113
,',:0 .U::! ..:.~¡)
,.....
G
4­
t'",IrH(".t1'.> r.:lr;
4:::."
':7Q
4¡m
l.:;~
¡,l
;¡':):I:::J '":'"!,:-n(H
---_._-­~,jJ
':'':Jt)
5:)(\
-;'20
:!.5 ~.!;n 1~:::1
f8 '15
1'r22 11):;' r91)1 rSIj-J ~1)'J<)71
23
i9,!5 ;¿O 0521 12 22,"l~ 2~~,4
::! j,
:2!.,~3 2i;.Si
H~.s5
le.?6
1323 2;},¡.i) 2!{:& 21,90 2t, 10 2S:29
21j~6 L'taS 2tHl2 !~·~7:31
:9.11 ¡'>,G216~ 1}12 (1).:
le l'l
n D ;').'~ N
2\DlZZ~Ol~!52:6121l6.le~30(.,jJ':'f¡~2QJ:;"41Gl!..H~G1-l
~_l_,?: ~~~~_ 1418 ¿s 11
W68 ;'':111 JI SI
~"2l:rí
J']
H3
}.:.~~ :.6 T'J
39
j.oM:U.?Z40615'o;7c;r;:~eS$:l:10~:J'
JSai
ro',
~, 71 ~l:5.l ZA?
Ii)
'17
U,
lS,;;'l
l,
a;ea
~n:t2 2~4.5 3~G2
j!
¡:-1!:'¡
2S"~':'-::-+I'rgj ¡!t4O,
P¡Jr,)
l~
IJE¡
JO
t.J
:::i'.
;.,l:;
pa:nc
tr.ln3IT\i~:~H'l;:' tt1d,c:.1éiU ¡;on
CO;G"~ntjJ
l~ ~oC':C1rp
es; y,,-,,q.c1tl:::.-';e el
;n!,;(,Qr
Tabla 8 6 (con;inu;,::iÓn]. _. Prestaciones de 1.05 Correa" Tr:.!l'cdales OLEOST A,te:
--...,..---_._--~--_._--_.-.~-----_. , ' - - '
._._--~--
p·f ~'T ~~(:;c.r:
~,t...
._ ......
p::,au
....
-
jC
'J
::.;:'''I¡<;fif':'l:i
--'-::":'''-~-'----''-;~
j<!
57 el
(lO Ji}
[,2 f)~
~~)
!J
6l,l~
(¡J
72 J¿ ;.: "'2 76
~~I
,:)
79.;J
73~¡·)
7:)
~.:) >~
7179
é25;
5B5
S(i.::;¡2 S'J't:.7
eco
51 : 1)
6~O
Sl;¡; t,D
~~
~,
1]
,,1
~;--!
1),;
&:J :J ,~5
el
f,~":';
_
.33 E'::
!
5,~ ~l
::;s
~:) (~7("""'---'
'.:~
~--"-~_:_-
tPJ
71
2S.+_ _t __ r
,
/
.. ..;i.JÚ
.. J
t,O
1-4 6ó':C Qeg;.
j.~
'l'SD
Si L! 1,,0 (/) id
c:..l:
:'S .¡'; ;~;)
r
I
¡~
G. -
fJC!(.H·"~
,J'"
t:ttrrt:C.ciun C~ p~r~ ¡-¡rLOS d,~ (:únL,<:H, ¡HfC'tjon:~ ~ 12.0'.
-----\7d
lLlf, •. fI,:_~,~<f\
1',:p¡lf'l'
;:,~);~,I;J):':,',j\
l·.)
Ú
,'",',
')
C./(¡
\(,1)
?~J (1 "'lí~ P q'j
71
:9
Ú
!:v
IJ'~'
':11 G:~;? ", !::' f¡,rt.:"
Q,n1
f::G G¡q D_~¿ LV)
,--~---
--l
•..',':'
I~IJ'
':oS
---
t,e·'
1()
¡ :~)
CdL:
o ,:,:f,; o 7i
¡')J
f¡
in;}
.....
_~
.........
_---~
.
I"¡'J
;j: \1;,( e.l.\!
r,t,~ ':'.';'~ ~;t 1)7C
f:
--~~_
ItJ~"
~-_.~
71:
PROBLEMAS
l. Se tiene una despulpador
movida por un motor e
transmisión en forma co
condiciones:
a). Distancia máxima entre
b). Distancia mínima entre
c). La potencia del motor
debe ser reales.
d). Las horas de trabajo
asumirse en forma real.
Debe hacerse un grafi
condiciones de la transm
* Base para el motor.
'1< Sistema de sujeción del mot
* Distancia entre centros, etc.
e). f).
Costo del sistema compl
2. Se requiere instalar un tra
las siguientes característica
a). Dias de molienda por sema
b) Horas de molienda por dia:
c). Carga de panela por día: 12
d). Motor de combustión intern
e).
Distancia entre ejes: má
Con base a lo anterior y asu
más real posible, usted debe d
y su motor; en forma completa
* Tipo de transmisión.
* Costos.
* Normas mínimas de funcion
* Esquema claro con datos
sistema, motor, trapiche, tr
3.
Seleccionar una transm
eléctrico de 25hp,
funcionamiento y punta
maquina a 800rpm.
NOTA 1; Debe utilizar d
4. Dos bandas trapeciales
compuesta de una pol
1200 rpm y una polea
capacidad o potencia d
servicio de 1.25 y en la d
Una cadena de rodillos N
desde una nleda catarin
relación de velocidades es
a). Calcule la
transmisión.
potencia
n
b). Evalúe la tensión de la ca
el.
Cual es el factor
s
resistencia mínima a la tensi
d). Cual debe ser la longitud
será de 20pulgadas?
ej. Estime el valor del esfuer
en un rodillo; considere que
punto de contacto es muy gr
6. Un piñón de 21 dientes
pulgada, gira aliSO rp
Determínese el numero d
teórica entre centros.
7. Un piñón de 19 dientes
velocidad de 1
rpm
aproximadamente a 470
número de dientes de la r
8. Un engranaje de dos ele
pulgada y una relación de
Calcúlese el número de
diametral y la distancia te
9. Los engranajes indicado
diametral 3 y ángulo de
piñón gira en sentido con
25hp, a través del engr
Calcúlese la reacción resu
libre de 36 dientes.
10. Una banda plana tiene
espesor y transmite 15hp.
en un plano horizontal a u
tiene 6pulgadas de diáme
lado colgante (o flojo) de
polea impulsada tiene 18p
de la banda es de 0,035 lib
al.Determine la tensión en
el coeficiente de fricción es
b). Que tensiones resultar
que el coeficiente de f
deslizamiento en la banda
cl. Calcule la longitud de la
11. Una banda plana, provi
elastomero, mide 200mm
velocidad de 25 m/ s. La
elemento de transmisión
conectar una polea impul
impulsada de 900mm de
6m.
al.Calcule la longitud de la
b).Obtenga las tensiones e
fricción de 0.38.
12. Una transmisión de ban
colado de 4pies de diámetr
tamaño de banda satisfa
velocidad de polea de 380
13. Una banda plana hecha d
de ancho, y conecta un
16pulgadas, con una
configuración usual o abie
si la velocidad de la band
maxlma se puede trans
tensiones resultantes en la
14. Se seleccionará una band
transmisión motriz de un t
solo cilindro y 5hp cuando
transmitida por la band
6.2pulgadas, y la polea
motor se controla media
Se empleará un sistema
de contacto sean de 18
especifiquela mediar, te