Las distribuciones Normal y binomial. La distribución NORMAL Las

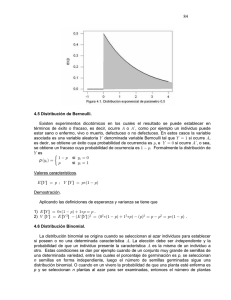
Las distribuciones Normal y binomial.
La distribución NORMAL
Las variables continuas cuyos valores dependen de un gran número de factores
independientes y cuyas influencias se compensan entre sí haciendo que prevalezca el tipo
medio, suelen seguir la distribución Normal.
La distribución Normal es idónea para explicar:
comportamientos sociales (aceptación de normas, gusto por la costumbres, etc.)
actitudes económicas(consumo, impacto de un producto etc.)
aptitudes psicológicas(cociente intelectual, etc.)
medidas antropométricas (estatura, peso, etc.)
medidas morfológicas (tamaño de los frutos de un árbol, etc.)
errores cometidos en las mediciones
La distribución Normal Estándar N(0,1).
Cuando una distribución normal tiene su media igual a 0 y su desviación típica igual a 1, se la
conoce como distribución Normal Estándar. La variable que sigue esta distribución se llama
tipificada y se la representa con Z.
La áreas bajo la curva normal tipificada se calculan usando las tablas de la curva normal.
Las tablas dan el área bajo la curva desde -∞ a K. El valor del área se encuentra en el cruce
de la columna que contiene las unidades y décimas de K con la fila de las centésimas.
Propiedades de la distribución Normal
• Su campo de existencia es la recta real R.
• Es simétrica respecto de su media μ .
• Tiene un máximo que coincide con su media, moda y mediana
• En μ+σ y μ-σ tiene los puntos de inflexión.
• El área bajo la curva es 1 y entre los puntos:
μ+ σ y μ- σ es 0,6826
μ+2σ y μ-2σ es 0,9544
μ+3σ y μ-3σ es 0,9972
Tipificación
Si la variable estudiada X, sigue una distribución N(μ,σ), para trabajar con las tablas de la
Curva normal tipificada, es necesario tipificar la variable X, para ello definimos la variable Z
X-μ
Z=
--------σ
Uso de las tablas N(0,1)
P(X≤1,75) = 0,9599, cruce fila de 1,7 y columna de 0,05
P(1≤X≤1,85)= P(X≤1,85)-P(X≤1)=0,9678-0,8413=0,1265
Si la variable no está tipificada, por ejemplo N(5,3), se la tipifica antes de buscar en las tablas.
P(X≤8)= P(X-5/3≤8-5/3)=P(Z≤1)=0,8413
Distribución Binomial
Muchos experimentos sociales dan como resultado dos sucesos complementarios:
ser hombre/mujer;
tener mas de 18 años/menos de 18 años;
tener trabajo remunerado/ no tener trabajo remunerado, etc
A las dos posibilidades de estos sucesos contrarios entre si se les llama éxito y fracaso.
La distribución de la probabilidad de este tipo de sucesos se llama Distribución Binomial y
sus propiedades son:
a) Cada prueba del experimento aleatorio tiene dos posibles resultados: éxito (E) o fracaso (F)
b) Se realizan n pruebas del experimento, independientes entre sí
c) La probabilidad de éxito es siempre la misma a lo largo de las n pruebas, se denota como p.
Y la probabilidad de fracaso será siempre 1-p = q
d) La variable aleatoria X que cuenta el número r de éxitos ( r = 0, 1, 2,… n) en pruebas tomará
los valores 0, 1, 2, … n
Tal variable binomial queda definida con los parámetros n y p y se escribe B(n,p)
Si el experimento se hace una vez n =1 , puede haber 0 o 1 éxito
P(X=1) = P(E) = p
P(X=0) = P(F) = 1 – p = q
Si el experimento se hace dos veces n=2, puede haber 0 , 1 o 2 éxitos
P(X=2 ) = P(EE) = p . p = p2
P(X=1) = P( EF + FE ) = pq + qp = 2 pq
P (X=0 ) = P( FF) = qq = q2
Si el experimento se hace tres veces n=3, puede haber 0 , 1 , 2 o 3éxitos
P(X=3 ) = P(EEE) = p . p . p = p3
P(X=2) = P( EEF + FEF + FFE ) = pq q + qpp + qpp = 3 p2q
P (X=1) = P( EFF + FEE + FFE) = pqq + qpp + qqp = 3 p q2
P (X=0 ) = P( FFF) = q.q .q = q3
Los términos que vamos obteniendo coinciden con los términos del desarrollo de las sucesivas
potencias de ( p + q )
( p + q )1 =
p + q
( p + q )2 =
p 2 + 2 p. q + q2
( p + q )3 =
p 3 + 3 p 2 q + 3 p q 2 p + q3
Recordando la fórmula del desarrollo del binomio de Newton:
Distribución Binomial
Muchos experimentos sociales dan como resultado dos sucesos complementarios:
ser hombre/mujer;
tener mas de 18 años/menos de 18 años;
tener trabajo remunerado/ no tener trabajo remunerado, etc
A las dos posibilidades de estos sucesos contrarios entre si se les llama éxito y fracaso.
La distribución de la probabilidad de este tipo de sucesos se llama Distribución Binomial y
sus propiedades son:
a) Cada prueba del experimento aleatorio tiene dos posibles resultados: éxito (E) o fracaso (F)
b) Se realizan n pruebas del experimento, independientes entre sí
c) La probabilidad de éxito es siempre la misma a lo largo de las n pruebas, se denota como p.
Y la probabilidad de fracaso será siempre 1-p = q
d) La variable aleatoria X que cuenta el número r de éxitos ( r = 0, 1, 2,… n) en pruebas tomará
los valores 0, 1, 2, … n
Tal variable binomial queda definida con los parámetros n y p y se escribe B(n,p)
Si el experimento se hace una vez n =1 , puede haber 0 o 1 éxito
P(X=1) = P(E) = p
P(X=0) = P(F) = 1 – p = q
Si el experimento se hace dos veces n=2, puede haber 0 , 1 o 2 éxitos
P(X=2 ) = P(EE) = p . p = p2
P(X=1) = P( EF + FE ) = pq + qp = 2 pq
P (X=0 ) = P( FF) = qq = q2
Si el experimento se hace tres veces n=3, puede haber 0 , 1 , 2 o 3éxitos
P(X=3 ) = P(EEE) = p . p . p = p3
P(X=2) = P( EEF + FEF + FFE ) = pq q + qpp + qpp = 3 p2q
P (X=1) = P( EFF + FEE + FFE) = pqq + qpp + qqp = 3 p q2
P (X=0 ) = P( FFF) = q.q .q = q3
Los términos que vamos obteniendo coinciden con los términos del desarrollo de las sucesivas
potencias de ( p + q )
( p + q )1 =
p + q
( p + q )2 =
p 2 + 2 p. q + q2
( p + q )3 =
p 3 + 3 p 2 q + 3 p q 2 p + q3
Recordando la fórmula del desarrollo del binomio de Newton:
(p+q)
n
= n p n + n p n-1 q + n pn - 2
0
1
2
q2
+ …. + n p q n—1 + n q n
n -1
n
La probabilidad de r éxitos P (X = r ) = n pr q n - r
La tabla de la distribución binomial se puede usar para hacer los cálculos con mayor rapidez
aunque las tablas casi nunca dan valores mayores que 20
Media y varianza de la distribución binomial
La media es siempre n . p
La varianza es (n . p . q) y su raíz cuadrada es la desviación típica
Cuando n va creciendo la distribución binomial se acerca mucho a la Normal, por lo que se
puede usar la tabla de la Normal para calcular los valores de la binomial. Esto se verifica
siempre que los productos n . p y n. q son mayores o iguales a 5 y la aproximación es muy
muy buena si p es cercano a 0’5.
B(n,p) se ajustará con N ( np , V npq)
Se recomienda visitar:
http://personal5.iddeo.es/ztt/Tem/t19_distribucion_binomial.htm
http://sauce.cnice.mecd.es/~jpeo0002/Archivos/PDF/T03.pdf