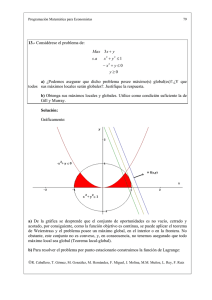
λ λ λ λ λ ∂λ ∂ λ λ λ ∂ ∂ λ λ ∂ ∂ ∂λ ∂ λ ∂ ∂ λ

Programación Matemática para Economistas
69
10.- Una empresa desea maximizar los ingresos que obtiene con la exportación de sus dos
productos a un país vecino. El precio al que vende el producto 1 a dicho país depende de la
cantidad de toneladas exportadas al mismo y adopta la siguiente expresión p1 = 100 - x1,
mientras que el precio por tonelada del segundo producto es constante e igual a 50.
Determinar la cantidad de toneladas que debe exportar de cada producto teniendo en cuenta
que el país vecino ha puesto un límite a la cantidad de importaciones de esa empresa igual a
una constante b.
Solución:
El planteamiento del problema sería:
Max p1 x1 + p2 x 2 = Max (100 − x1 ) x1 + 50 x 2 = Max − x12 + 100 x1 + 50 x2
s. a x 1 + x 2 ≤ b
x1 , x 2 ≥ 0
Si consideramos las condiciones de punto estacionario para el caso de condiciones
de no negatividad obtenemos la función de Lagrange:
L ( x1 , x 2 , λ ) = − x12 + 100 x1 + 50 x 2 − λ ( x1 + x 2 − b)
con las condiciones:
∂L
= −2 x1 + 100 − λ ≤ 0
∂x1
∂L
(2)
= 50 − λ ≤ 0
∂x 2
∂L
(3)
= − x1 − x 2 + b ≥ 0
∂λ
x1 = 0

∂L
(4) x1
= x1 (-2 x1 + 100 − λ ) = 0 
∂x1
− 2 x1 + 100 − λ = 0
(1)
(5) x 2
(6) λ
x = 0
∂L
= x 2 (50 − λ ) = 0  2
∂x 2
λ = 50
λ = 0 contradice(2)
∂L
= λ (- x1 − x 2 + b) = 0 
x1 + x 2 = b
∂λ

(7 ) λ ≥ 0
(8) x1 , x 2 ≥ 0
Los posibles sistemas son:
R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz
Programación Matemática para Economistas
70
a) x1 = x2 = 0 y x1 + x2 = b, el cual no tiene sentido.
b) x1 = 0, λ = 50 y x1 + x2 = b, que genera el punto (0, b, 50)
c) 2x1 -100 +λ = 0, x2 = 0 y x1 + x2 = b, del que se obtiene el punto (b, 0, 100-2b)
d) 2x1 -100 +λ = 0, λ = 50 y x1 + x2 = b, que produce el punto (25, b-25, 50).
Los puntos son (0, b, 50), (b, 0, 100-2b) y (25, b-25, 50).
El primero incumple (1), luego no es punto estacionario. El segundo para ser punto
estacionario, por (2) b debe ser menor o igual que 25 y el tercero debe cumplir que b sea
mayor o igual a 25.
Por tanto, los puntos estacionarios son:
(b, 0, 100-2b)
b ≤ 25
y
(25, b-25, 50)
b ≥ 25
y si b =25 ambos coinciden.
R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz
Programación Matemática para Economistas
71
Una vez obtenidos los puntos estacionarios, dependiendo del valor del parámetro b,
como la función objetivo es convexa y el conjunto de oportunidades también podemos
asegurar que los puntos estacionarios obtenidos son máximos.
R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz