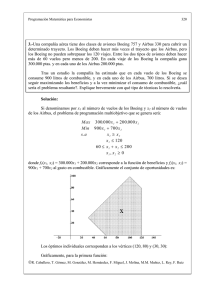
13.- Considérese el problema de: a) ¿Podemos asegurar que dicho

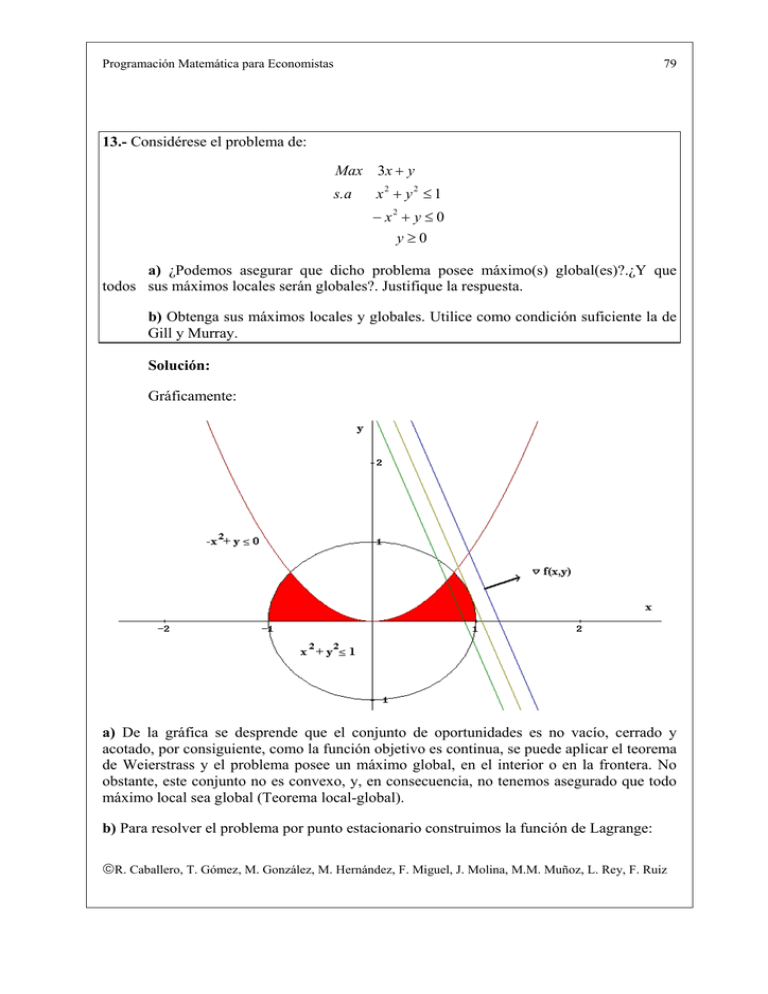
Programación Matemática para Economistas
79
13.- Considérese el problema de:
Max 3x + y
s. a
x2 + y2 ≤ 1
− x2 + y ≤ 0
y≥0
a) ¿Podemos asegurar que dicho problema posee máximo(s) global(es)?.¿Y que
todos sus máximos locales serán globales?. Justifique la respuesta.
b) Obtenga sus máximos locales y globales. Utilice como condición suficiente la de
Gill y Murray.
Solución:
Gráficamente:
a) De la gráfica se desprende que el conjunto de oportunidades es no vacío, cerrado y
acotado, por consiguiente, como la función objetivo es continua, se puede aplicar el teorema
de Weierstrass y el problema posee un máximo global, en el interior o en la frontera. No
obstante, este conjunto no es convexo, y, en consecuencia, no tenemos asegurado que todo
máximo local sea global (Teorema local-global).
b) Para resolver el problema por punto estacionario construimos la función de Lagrange:
R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz
Programación Matemática para Economistas
80
L ( x, y, λ1 , λ 2 , λ3 ) = 3x + y − λ1 ( x 2 + y 2 − 1) − λ 2 (− x 2 + y ) − λ3 (− y )
obteniéndose las condiciones:
∂L
= 3 − 2λ1 x + 2 xλ 2 = 0
∂x
∂L
(2)
= 1 − 2 yλ1 − λ 2 + λ3 = 0
∂y
∂L
(3)
= −x2 − y 2 + 1 ≥ 0
∂λ1
∂L
(4)
= x2 − y ≥ 0
∂λ2
∂L
(5)
= y≥0
∂λ3
∂L
(6) λ1
= −λ1 ( x 2 + y 2 − 1) = 0
∂λ1
∂L
(7 ) λ 2
= −λ 2 ( − x 2 + y ) = 0
∂λ2
∂L
(8) λ3
= λ3 ( y ) = 0
∂λ3
(9) λ1 , λ 2 , λ3 ≥ 0
(1)
Observando el desplazamiento de las curvas de nivel, podemos situar el óptimo del
problema sobre la circunferencia y, por tanto, sólo la primera restricción será activa en
dicho punto. En consecuencia, las condiciones de holgura quedarían:
x 2 + y 2 − 1 = 0,
λ 2= 0,
λ 3= 0
las cuales junto con las expresiones (1) y (2) nos llevan al punto:
3 2 2 5

,
, , 0, 0

2 5 2 5 2

En orden a comprobar la condición suficiente local y, ya que, como hemos
comentado previamente, en ese punto estacionario la única restricción activa es la que
corresponde a la circunferencia, siendo el multiplicador asociado estrictamente positivo,
tenemos que clasificar, en dicho punto, la forma cuadrática:
R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz
Programación Matemática para Economistas
81
 − 2λ 1
Φ (h1 , h2 ) =(h1 , h2 )
 0
h 
s.a (2 x, 2 y ) 1 = 0.
 h2 
  h1 
 
− 2λ 1   h2 
0
que corresponde a:
Φ (h1 , h2 ) =−
s.a
3 2
5
h1 +
2 5
2
2
5
h12 −
2 5
2
h22
h2 = 0.
la cual es definida negativa.
3 2 2 5

,
, , 0, 0 es máximo local del problema, y, por
Luego, el punto 
2 5 2 5 2

consideraciones análogas a las del problema anterior, máximo global.
R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz