Solución - IES Francisco Ayala

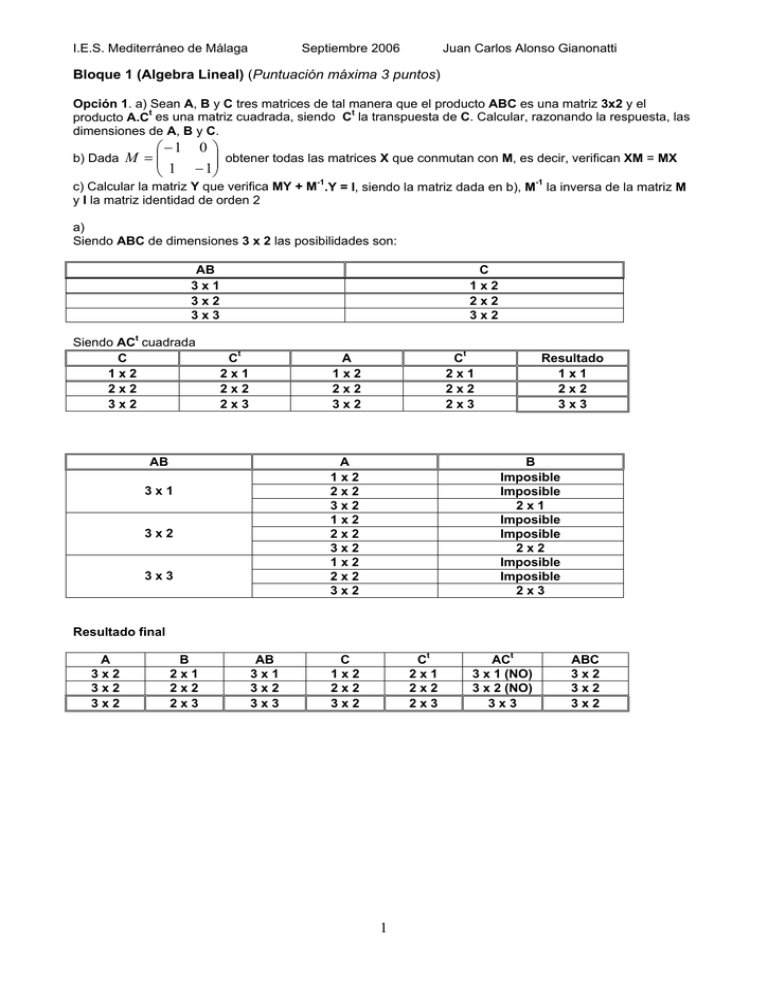
I.E.S. Mediterráneo de Málaga
Septiembre 2006
Juan Carlos Alonso Gianonatti
Bloque 1 (Algebra Lineal) (Puntuación máxima 3 puntos)
Opción 1. a) Sean A, B y C tres matrices de tal manera que el producto ABC es una matriz 3x2 y el
producto A.Ct es una matriz cuadrada, siendo Ct la transpuesta de C. Calcular, razonando la respuesta, las
dimensiones de A, B y C.
−1
b) Dada M = 
1
0
 obtener todas las matrices X que conmutan con M, es decir, verifican XM = MX
− 1
c) Calcular la matriz Y que verifica MY + M-1.Y = I, siendo la matriz dada en b), M-1 la inversa de la matriz M
y I la matriz identidad de orden 2
a)
Siendo ABC de dimensiones 3 x 2 las posibilidades son:
AB
3x1
3x2
3x3
Siendo ACt cuadrada
C
1x2
2x2
3x2
C
1x2
2x2
3x2
Ct
2x1
2x2
2x3
Ct
2x1
2x2
2x3
A
1x2
2x2
3x2
AB
A
1x2
2x2
3x2
1x2
2x2
3x2
1x2
2x2
3x2
3x1
3x2
3x3
Resultado
1x1
2x2
3x3
B
Imposible
Imposible
2x1
Imposible
Imposible
2x2
Imposible
Imposible
2x3
Resultado final
A
3x2
3x2
3x2
B
2x1
2x2
2x3
AB
3x1
3x2
3x3
Ct
2x1
2x2
2x3
C
1x2
2x2
3x2
1
ACt
3 x 1 (NO)
3 x 2 (NO)
3x3
ABC
3x2
3x2
3x2
I.E.S. Mediterráneo de Málaga
Septiembre 2006
Juan Carlos Alonso Gianonatti
Continuación de la Opción 1 del Bloque 1
b)
−b  − a + b −b
a b  −1 0  a b  a b  −1 0   − a
 ⇒ 
 ⋅ 
 = 
 ⋅ 
 ⇒ 
 = 
 ⇒
Sea X = 
 c d   1 − 1  c d   c d   1 − 1  a − c b − d   − c + d − d 
 − a = −a + b ⇒ b = 0

− b = −b
λ 0


⇒ X = 

a
c
c
d
a
d
µ
λ
−
=
−
+
⇒
=



 b − d = −d ⇒ b = 0
c)
(
)
(
)(
Y M + M −1 = I ⇒ Y M + M −1 M + M −1
)
−1
(
= I M + M −1
)
−1
(
⇒ YI = M + M −1
)
−1
(
⇒ Y = M + M −1
)
−1
−1 0
−1 1 
−1 0 
1
 ⇒ adj M t = 

= 1 ≠ 0 ⇒ Existe M −1 ⇒ M −1 =
⋅ adj M t ⇒ M t = 
1 −1
M
 0 − 1
 − 1 − 1
−1 0  −1 0  − 2 0 
1 −1 0  −1 0 
 ⇒ 
 ⇒ M + M −1 = 
 + 
 = 
 ⇒
= ⋅ 
1  − 1 − 1   − 1 − 1
 1 − 1  − 1 − 1  0 − 2 
(
M =
M −1
M + M −1 =
−2 0
= 4 ≠ 0 ⇒ Existe M + M −1
0 −2
(
)
−1
)
(
⇒ M + M −1
)
−1
=
1
M +M
−1
[
(
⋅ adj M + M −1
)]
t
− 2 0 
− 2 0 
t
 ⇒ adj M + M −1 = 
 ⇒
= 
 0 − 2
 0 − 2

 1
0 
−
2
0
−


−
1
1

= 2
Y = M + M −1 = 
4  0 − 2   0 − 1 


2

(M + M )
(
−1 t
(
)
)
Opción 2.a) Si un sistema de tres ecuaciones lineales con tres incógnitas, el rango de la matriz de los coeficientes es
3, ¿podemos afirmar que el sistema es compatible? Razona la respuesta.
b) Discute, segundo los valores del parámetro m, el sistema de ecuaciones lineales:
 y + mz = 0

 x+z =0
mx − y = m

c) Resuelve el sistema anterior para el caso en que m = 0
a) El sistema es Compatible Determinado, porque eso determina que el rango de la matriz ampliada sea
también 3, al coincidir el rango de las dos matrices es Compatible tal como determina el teorema de Rouche
y como este valor es igual al número de incógnitas y, según la regla de Cramer, tiene una solución única
b)
0 1
m 0  0 1 m 0 

 

A = 1 0 1 = m − m = 0 ⇒ 1 0
1 0  ≡ 1 0 1 0  ⇒
0 −1 − m m 0 0 0 m
m −1 0

 

m ≠ 0 ⇒ rang ( A) = 2 ≠ rang ( A) = 3 ⇒ Sistema Incompatible


m = 0 ⇒ rang ( A) = rang ( A / B ) = 2 < Número de incógnitas ⇒ Sistema Compatible In det er min ado
0
1
m
Continuación de la Opción 2 del Bloque 1
2
I.E.S. Mediterráneo de Málaga
Septiembre 2006
Juan Carlos Alonso Gianonatti
b) Si m = 0 ⇒ Sistema hom ogéneo ⇒ Sistema Compatible In det er min ado
 0 1 0 0  0 1 0 0

 

 1 0 1 0  ≡  1 0 1 0  ⇒ y = 0 ⇒ x + z = 0 ⇒ x = − z ⇒ Solución ⇒ (x , y , z ) = (− λ , 0 , λ )
 0 −1 0 0  0 0 0 0

 

Bloque 2 (Geometría) (Puntuación máxima 3 puntos)
Opción 1.a) Dados los vectores u = (1 , 0 , − 1) , v = (1 , 1 , 0 ) , calcula los vectores unitarios de
ortogonales a los dos vectores dados.
ℜ 3 que son
b) Sea π el plano determinado por el punto P(2 , 2 , 2) y los vectores u = (1 , 0 , − 1) , v = (1 , 1 , 0 ) .Calcula
el ángulo que forma el plano π con la recta que pasa por los puntos
O(0 , 0 , 0) y Q(2 , -2 , 2).
c) Calcula el punto simétrico de O(0 , 0, 0) respecto del plano x - y + z - 2 = 0.
a) Es el vector w perpendicular a ambos vectores y lo calcularemos hallando el producto vectorial de los
dos, seguidamente lo normalizaremos
i j k
u = (1 , 0 , − 1)
⇒ w = u ∧ v = 1 0 − 1 = − j + k + i = i − j + k ⇒ w = (1 , − 1 , 1) ⇒

 v = (1 , 1 , 0 )
1 1 0
 1
1
1   3
3
3
2

,−
,
,−
,
 ≡ 
w = 12 + (− 1) + 12 = 3 ⇒ w = 
3 
3
3
3  3
 3
b) El vector director del plano
π , que es perpendicular a él y a los dos vectores dados, fue calculado en el
apartado a) es igual a w , que siendo, a la vez, perpendicular al vector PG, siendo G el punto genérico del
plano y eso tiene como consecuencia que su producto escalar es nulo y la ecuación del plano pedido.
El ángulo entre plano π y el vector OQ es el formado por el vector director de este con el vector director de
aquel que es el producto escalar de ambos entre el producto de sus módulos, siendo el valor calculado el
seno del ángulo α que forman.

vπ = w = (1 , − 1 , 1)
⇒ vπ ⊥ PG ⇒ vπ ⋅ PG = 0 ⇒

 PG = (x , y , z ) − (2 , 2 , 2 ) = (x − 2 , y − 2 , z − 2 )
(1 , − 1 , 1) ⋅ (x − 2 , y − 2 , z − 2) = 0 ⇒ x − 2 − y + 2 + z − 2 = 0 ⇒ π ≡ x − y + z − 2 = 0
vπ ⋅ OQ

(1 , − 1 , 1) ⋅ (2 , − 2 , 2)
vπ = w = (1 , − 1 , 1)
⇒ sen (α ) =
=

2
2
OQ = (2 , − 2 , 2 ) − (0 , 0 , 0 ) = (2 , − 2 , 2 )
vπ ⋅ OQ
12 + (− 1) + 12 ⋅ 2 2 + (− 2 ) + 2 2
sen (α ) =
2+2+2
3 ⋅ 12
=
6
36
= 1 ⇒ α = arc sen 1 = 90º =
3
π
2
rad ⇒ Son perpendiculares
I.E.S. Mediterráneo de Málaga
Septiembre 2006
Juan Carlos Alonso Gianonatti
Continuación de la Opción 1 del Bloque 2
c) Hallaremos una recta r, perpendicular al plano α dado, y por ello su vector director es el del plano que
pase por O.
Calcularemos el punto P de corte de la recta r hallada y el plano que es el punto medio entre O y su
simétrico O’
 x=λ
2

v r = vα = (1 , − 1 , 1) ⇒ r ≡  y = −λ ⇒ Punto P ⇒ λ − (− λ ) + λ − 2 = 0 ⇒ 3λ − 2 = 0 ⇒ 3λ = 2 ⇒ λ =
3
 z=λ

4
2
 2 0 + xo '

 3 = 2 ⇒ xo ' = 3
 x=3
 2 0 + y

4 4
4
2
4
o'
P  y = − ⇒ − =
⇒ y o ' = − ⇒ O'  , − , 
3 3
2
3
3
3
 3

z
+
0
2
2
4
o
'

 z=
=
⇒ zo' =

 3
3
2
3
Opción 2.- Los lados de un triángulo están sobre las rectas:
x = 2 + t
x − y − z − 1 = 0
x −1 y −1 z +1

r1 :
=
=
; r2 :  y = 2 + t ; r3 : 
1
−1
2
 x−z =0
 z = −1

a) Calcula los vértices del triángulo. ¿Es un triángulo rectángulo? Razona la respuesta
b) Calcula la ecuación del plano π que contiene el triángulo. Calcula la intersección del plano π con los ejes
OX, OY y OZ.
a) Hallaremos los puntos de corte A, B y C de las rectas entre si ya que tienen que cortarse para formar
triángulo. Una vez hallado los vértices y para estudiar si son triángulo rectángulo veremos si los vectores AB
y AC lo son para ello hallaremos su producto escalar que tiene que ser nulo, de no serlo estudiaremos si lo
es el formado por los vectores BA y BC, y finalmente analizarlo con CA y CB, de no dar ninguno nulo no
será triángulo rectángulo
x − y − z − 1 = 0
r3 : 
⇒ − y − 1 = 0 ⇒ y = −1 ⇒ − x + z = 0 ⇒ x = z
 − x+ z =0
  x =1+ λ
 
r1 :  y = 1 − λ
1+ λ = 2 + t
 x =1+ 0
  z = −1 + 2λ
1 + 0 = 2 + t ⇒ t = −1


⇒  1 − λ = 2 + t ⇒ 2λ = 0 ⇒ λ = 0 ⇒ 
⇒ A y = 1 − 0

x = 2 + t
1 − 0 = 2 + t ⇒ t = −1
− 1 + 2λ = −1
 z = −1 + 2 ⋅ 0




 r2 :  y = 2 + t

 z = −1


  x =1+ λ
 
r1 :  y = 1 − λ
 1+ λ = µ
 x =1+ 2
  z = −1 + 2λ
 1+ 2 = µ ⇒ µ = 3


⇒  1 − λ = −1 ⇒ −λ = −2 ⇒ λ = 2 ⇒ 
⇒ B y = 1 − 2

µ
x
=

− 1 + 2 ⋅ 2 = µ ⇒ µ = 3
− 1 + 2 λ = µ
 z = −1 + 2 ⋅ 2




 r3 :  y = −1

z=µ


4
I.E.S. Mediterráneo de Málaga
Septiembre 2006
Juan Carlos Alonso Gianonatti
Continuación de la Opción 2 del Bloque 2
a)Continuación
 x = 2 + t
 
r2 :  y = 2 + t
2 + t = µ
 x = −1
  z = −1
2 + t = −1 ⇒ t = −3


⇒ 2 + t = −1 ⇒ 
⇒ C  y = −1

x
µ
=

2 + t = −1 ⇒ t = −3
 −1 = µ
 z = −1




 r3 :  y = −1

z=µ


 AB = (3 , − 1 , 3) − (1 , 1 , − 1) = (2 , − 2 , 4 ) ≡ (1 , − 1 , 2 )
⇒ AB ⋅ AC = (1 , − 1 , 2 ) ⋅ (1 , 1 , 0 ) = 1 − 1 = 0

 AC = (− 1 , − 1 , − 1) − (1 , 1 , − 1) = (− 2 , − 2 , 0 ) ≡ (1 , 1 , 0 )
AB ⊥ AC ⇒ Es un triángulo rectángulo
b) El plano π queda determinado por los vectores AB, AC y AG siendo G el punto genérico del
plano. Estos tres vectores son coplanarios (pertenecen al mismo plano) y el vector AG es combinación
lineal de los otros dos, por eso el determinante de la matriz formada por ellos es nulo y la ecuación pedida
del plano

AB = (1 , − 1 , 2 )
x −1 y −1 z +1

⇒π ≡ 1
−1
2 = 0⇒
AC = (1 , 1 , 0 )

 AG = (x , y , z ) − (1 , 1 , − 1) = (x − 1 , y − 1 , z + 1)
1
1
0

2 ( y − 1) + (z + 1) + (z + 1) − 2 (x − 1) = 0 ⇒ −2 (x − 1) + 2 ( y − 1) + 2 (z + 1) = 0 ⇒
(x − 1) − ( y − 1) − (z + 1) = 0 ⇒ π ≡ x − y − z − 1 = 0
Puntos de corte del plano π con los ejes
x = α
x =1


OX ≡  y = 0 ⇒ α − 0 − 0 − 1 = 0 ⇒ α − 1 = 0 ⇒ α = 1 ⇒ X  y = 0 ⇒ X (1 , 0 , 0 )
z = 0
z = 0


x = 0
x=0


OY ≡  y = β ⇒ 0 − β − 0 − 1 = 0 ⇒ − β − 1 = 0 ⇒ β = −1 ⇒ Y  y = −1 ⇒ Y (0 , − 1 , 0 )
z =0
z=0


x = 0
x=0


OZ ≡  y = 0 ⇒ 0 − 0 − γ − 1 = 0 ⇒ −γ − 1 = 0 ⇒ γ = −1 ⇒ Z  y = 0 ⇒ Z (0 , 0 , − 1)
z = γ
 z = −1


5
I.E.S. Mediterráneo de Málaga
Septiembre 2006
Juan Carlos Alonso Gianonatti
Bloque 3 (Análisis) (Puntuación máxima 4 puntos)
Opción 1.- a) Calcula los valores de a y b para que a gráfica de f ( x ) = ax +
b
tenga un mínimo relativo en
x
1 
, 4  , Para esos valores de a y b, calcula: asíntotas e intervalos de crecimiento y decrecimiento
2 
el punto 
de ƒ(x).
b) Calcula lim
x →0
x 2e x
cos 2 x − 1
c) Definición de primitiva e integral indefinida de una función. Enunciado de la regla de Barrow
a)
 1
1 b
a
a + 4b
 f  2  = 4 ⇒ a ⋅ 2 + 1 = 4 ⇒ 2 + 2b = 4 ⇒ 2 = 4 ⇒ a + 4b = 8
  
b
ax 2 − b

2
f ' (x ) = a − 2 =
⇒
⇒
2
1
b
b


x
x
f
'
0
a
0
a
0
a
4
b
0
=
⇒
−
=
⇒
−
=
=
⇒
−

 
2
1
2

1



4
2

a + 4b = 8
1 4x 2 + 1
⇒ 2a = 8 ⇒ a = 4 ⇒ 4 − 4b = 0 ⇒ 4b = 4 ⇒ b = 1 ⇒ f ( x ) = 4 x + =

x
x
a − 4b = 0
x = 0 ⇒ f (x ) =
4 ⋅ 02 + 1 1
= ⇒ No tiene solución ⇒ Asíntota vertical en x = 0
0
0
A sin tota horizontal
4x 2 + 1 ∞
8x
Aplicando L ' Hopital
= = 
  → = lim
= 8⋅∞ = ∞ ⇒
x →∞
x →∞ 1
x
∞
No existe a sin tota horizontal cuando x → ∞
y = lim
4x 2 + 1
∞
8x
Aplicando L ' Hopital
=
= 
  → = lim
= 8 ⋅ (− ∞ ) = −∞ ⇒
x → −∞
x → −∞ 1
x
−∞
No existe a sin tota horizontal cuando x → −∞
y = lim
A sin tota oblicua
4x 2 + 1
4x 2 + 1 ∞
8x
f (x )
Aplicando L ' Hopital
x
= lim
= lim
= = 
  → = lim
=4
m = lim
2
x →∞
x
→
∞
x
→
∞
x
→
−∞
x
∞
2x
x
x
 4x 2 + 1

4x 2 + 1 − 4x 2
1 1
n = lim[ f ( x ) − mx ] = lim 
− 4 x  = lim
= lim = = 0
x →∞
x →∞
x →∞ x
x
∞
 x
 x →∞
Existe a sin tota oblicua, y = 4 x cuando x → ∞
6
I.E.S. Mediterráneo de Málaga
Septiembre 2006
Juan Carlos Alonso Gianonatti
Continuación de la Opción 1 del Bloque 3
a )Continuación
A sin tota oblicua
4x2 +1
2
f (x )
8x
Aplicando L ' Hopital
x = lim 4 x + 1 = ∞ = 
  → = lim
=4
m = lim
= lim
2
x → −∞ 2 x
x → −∞
x → −∞
x → −∞
∞
x
x
x
 4x2 +1

4x2 +1− 4x2
1
1
− 4 x  = lim
= lim =
=0
n = lim [ f ( x ) − mx ] = lim 
−∞
→
−∞
→
x → −∞
x → −∞
x
x
x
x −∞
 x

Existe a sin tota oblicua, y = 4 x cuando x → −∞
1

2 x + 1 > 0 ⇒ 2 x > −1 ⇒ x > − 2
(2 x − 1) (2 x + 1) > 0 ⇒  2 x − 1 > 0 ⇒ 2 x > 1 ⇒ x > 1
4x2 −1
>
⇒
0
Crecimiento ⇒ f ' ( x ) > 0 ⇒

x2
x2
2

2
⇒
∀
∈
ℜ
>
x
x
0


1
1
−
−∞
∞
2
2
1
x> −
(-)
(+)
(+)
2
1
x>
(-)
(-)
(+)
2
x2 > 0
Solución
(+)
(+)


Crecimiento ∀x ∈ ℜ /  x < −
(+)
(-)
1 
1
∪x > 
2 
2
(+)
(+)
Decrecimiento ∀x ∈ ℜ / −
1
1
<x<
2
2
b)
lim
x →0
x (2 + x ) e x
x 2e x
02 e0
0 ⋅1 0
2 xe x + x 2 e x
Aplicando L ' Hopital
=
=
lim
lim
=
=






→
=
=
=
x →0 2 ⋅ cos x (− sen x )
x →0 − 2 ⋅ cos x sen x
cos 2 x − 1 cos 2 0 − 1 12 − 1 0
(
)
(
0 ⋅ (2 + 0 ) e 0
2 + 2x) e x + 2x + x 2 e x
0
Aplicando L ' Hopital
=
= =    → = lim
=
x →0 − 2 ⋅ (− sen x ⋅ sen x + cos x ⋅ cos x )
− 2 ⋅ cos 0 sen 0 0
(2 + 4 x + x ) e = lim (2 + 4 x + x ) e
= lim
− 2 ⋅ cos 2 x
− 2 ⋅ (cos x − sen x )
2
x →0
2
x
2
2
x →0
x
=
7
(2 + 4 ⋅ 0 + 0 ) e
2
− 2 ⋅ cos 2 ⋅ 0
0
=
2⋅1
2
=
= −1
− 2 ⋅ cos 0 − 2 ⋅ 1
I.E.S. Mediterráneo de Málaga
Septiembre 2006
Juan Carlos Alonso Gianonatti
Continuación de la Opción 1 del Bloque 3
c)
Definición de función primitiva
Dadas dos funciones f(x) y F(x), definidas en un intervalo I = [a , b], diremos que F(x) es una función
primitiva de f(x) si la derivada de F(x) es la función f(x) en el intervalo I
F ( x ) es primitiva de f ( x ) en I ⇔ F ' (x ) = f (x ) , ∀x ∈ I
Definición de integral primitiva
Sea F(x) una primitiva de la función f(x) en el intervalo I = [a , b]; llamamos integral indefinida de f(x) al
conjunto de todas sus primitivas F(x) + C, siendo C un valor constante y lo representamos por:
∫ f (x ) dx = F (x ) + C
Regla de Barrow
Sea f(x) una función continua en [a , b], y sea F(x) una primitiva de f(x) en [a , b]; entonces:
b
∫ f (x ) dx = [F (x )]
b
a
= F (b ) − F (a )
a
Opción 2.a) Definición de función continua en un punto. ¿Que tipo de discontinuidad tiene en x = 0 la función
f (x ) =
x2
?.
x
b) Un alambre de 170 cm. de longitud se divide en dos partes. Con una de esas partes se quiere formar un
cuadrado y con la otra un rectángulo de tal manera que la base mida el doble de la altura. Calcula las
longitudes de las partes en las que se tiene que dividir el alambre para que la suma de las áreas del
cuadrado y del rectángulo sea mínima.
c) Calcula el área del recinto limitado por la recta y = 2 – x y la curva y = x2.
a) Una función f es continua en el punto x = x0 si, y solo si, verifica que: lim f ( x ) = f ( x 0 )
x → x0
Desglosando este concepto podremos dar una definición más precisa:
Una función f es continua en el punto x = x0 si verifica las siguientes condiciones:
- Existe f(x0), es decir la función está definida en x = x0
- Existe lim f ( x )
x → x0
-
Los dos valores anteriores coinciden esto es lim f ( x ) = f ( x 0 )
x → x0

x
0
0
=
= ⇒ Sin solución
 f (x ) =
x
0 0
⇒ Discontinuidad evitable Hay que redefinir la función

2
 lim f (x ) = lim x = 0 = lim x = 0
 x →0
x →0 x
0 x →0
2
x

⇒ f ( x ) =  x si x ≠ 0
 0 si x = 0
2
2
8
I.E.S. Mediterráneo de Málaga
Septiembre 2006
Juan Carlos Alonso Gianonatti
Continuación de la Opción 1 del Bloque 3
b) Sea C la base del cuadrado y H y B la altura y base, respectivamente del rectángulo
B = 2H


170 = 4C + 2 H + 2 B ⇒ 170 = 4C + 2 H + 2 ⋅ 2 H ⇒ 170 = 4C + 6 H ⇒ 85 = 2C + 3H ⇒ 2C = 85 − 3H ⇒

S = C 2 + BH = C 2 + 2 H ⋅ H = C 2 + 2 H 2

(85 − 3H ) + 8H 2 = 85 2 − 2 ⋅ 85 ⋅ 3H + 9 H 2 + 8H 2 = 17 H 2 − 510 H + 7225
 85 − 3H 
2
S =
 + 2H =
2
4
4
4


17 2
dS 17
17
17
S=
H − 30 H + 425 ⇒ S ' =
= (2 H − 30 ) = (H − 15) ⇒ Si S ' = 0 ⇒ (H − 15) = 0 ⇒
4
dH
4
2
2

H = 15 cm

d 2 S 17

H − 15 = 0 ⇒ H = 15 ⇒ S ' ' =
=
> 0 ⇒ Mínimo ⇒ 
B = 2 ⋅ 15 = 30 cm
2
dH 2

85 − 3 ⋅ 15 40
=
= 20 cm
C =
2
2
2
2
(
)
c)
2 − x = 0 ⇒ x = 2
Puntos de corte de las funciones con OX ⇒ y = 0 ⇒  2
 x =0⇒ x=0
Puntos de corte entre funciones ⇒ 2 − x = x 2 ⇒ x 2 + x − 2 = 0 ⇒ ∆ = 12 − 4 ⋅ 1 ⋅ (− 2 ) = 1 + 8 = 9 ≥ 0 ⇒
−1+ 3

=
=1
x

−1± 9
2
⇒
x=
−1− 3
2 ⋅1
x =
= −2
2

 y (0 ) = 2 − 0 = 2
x = 0 ∈ (− 2 , 1) ⇒ 
⇒ 2 > 0 ⇒ 2 − x > x 2 en el int ervalo (− 2 , 1)
2
(
)
0
0
0
y
=
=

A=
1 21
1 31
1
2
2
∫ (2 − x ) dx − ∫ x d = ∫ (2 − x − x ) dx = 2 ⋅ [x]−2 − ⋅ [x ]−2 − ⋅ [x ]−2
1
1
1
−2
−2
−2
A = 2 ⋅ [1 − (− 2 )] −
[
2
]
[
]
3
1 2
1
1
1
2
3
⋅ 1 − (− 2 ) − ⋅ 13 − (− 2 ) = 2 ⋅ (1 + 2 ) − ⋅ (1 − 4 ) − ⋅ [1 − (− 8)]
2
3
2
3
3 9
3 9
A = 6 + − = 3+ = u2
2 3
2 2
9