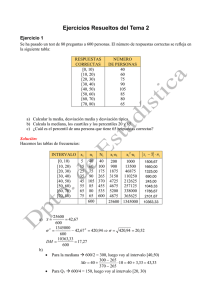
estadística

ESTADÍSTICA
Estadistica cover.indd 1
ESTADÍSTICA
2/18/08 11:14:25 PM
ESTADÍSTICA
Esenciales de... Estadística
D.R.© 2008 Lápiz Tinta Editores, S.A. de C.V.
Cda. de Seminario No. 53 México 01780, D.F.
Teoría y problemas de: Alejandro Fernández Gaos.
Con la colaboración de: Profesor Carlos Ramírez Torres.
D.R.© de esta edición, Editorial Santillana, S.A. de C.V.
Av. Universidad #767, 03100, México, D.F.
ISBN: 978-970-29-1715-1
Primera edición: Febrero de 2008.
Dirección Editorial: Clemente Merodio López.
Editora en Jefe de Bachillerato: Laura Milena Valencia Escobar.
Coordinación de Arte y diseño: Francisco Ibarra Meza.
Fotomecánica electrónica: Gabriel Miranda Barrón, Manuel Zea Atenco y Benito Sayago Luna.
La presentación y disposición en conjunto y de cada página del libro Esenciales de... estadística, son propiedad del editor.
Queda estrictamente prohibida la reproducción parcial o total de esta obra por cualquier sistema o método electrónico,
incluso el fotocopiado, sin autorización escrita del editor.
Miembro de la Cámara Nacional de la Industria editorial Mexicana.
Reg. Núm.802
Impreso en México.
Estadística
CAPÍTULOS
Unidad
1
INTRODUCCIÓN
Unidad
2
ESTADÍSTICA DESCRIPTIVA
11
Unidad
3
DATOS BIVARIADOS
63
Unidad
4
PROBABILIDAD
93
Unidad
5
DISTRIBUCIONES DE PROBABILIDAD
125
Unidad
6
DISTRIBUCIONES MUESTRALES
161
Unidad
7
INFERENCIA ESTADÍSTICA
179
1
iii
Contenido
1. Introducción
1
1.1. Estadística
1
Noción y utilidad
1.2. Variable
4
Dominio de una variable
Variable discreta
Variable continua
1.3. Población y muestra
6
Estadística descriptiva
Estadística inductiva
iv
1.4. Azar y probabilidad
7
•
8
Fenómenos deterministas y fenómenos aleatorios
2. Estadística descriptiva
11
2.1. Recopilación de datos
11
•
•
•
•
11
13
15
15
Tablas de distribución de frecuencias
Tablas de distribución porcentual
Tablas de distribución acumulativa
Tablas de distribución cualitativas
2.2. Representaciones gráficas
22
•
•
•
•
•
23
23
23
24
25
Histogramas
Gráfica de barras
Polígonos de frecuencias
Ojivas
Gráfica circular
Estadística
2.3. Medidas de tendencia central
29
•
•
•
•
•
Media aritmética
Media aritmética ponderada
Media aritmética para datos agrupados
Mediana
Moda
29
30
31
36
38
2.4. Medidas de dispersión y de posición
49
•
•
•
•
49
49
51
56
Rango o amplitud
Desviación media
Desviación estándar y varianza
Dispersión absoluta y relativa: coeficiente de variación
3. Datos bivariados
63
3.1. Relación entre dos variables
63
•
•
63
65
•
•
Variables cualitativas
Variables cuantitativas
Diagramas de dispersión
Relación lineal
Recta de mínimos cuadrados
Regresión lineal
70
72
3.2. Correlación lineal
82
•
•
82
86
Error estándar estimado
Coeficiente de correlación lineal
4. Probabilidad
•
•
•
93
4.1. Enfoques de la probabilidad
93
Subjetivo
Clásico
Frecuencial
93
93
94
v
Contenido
4.2. Posibilidades
96
•
96
•
•
100
102
103
4.3. Probabilidad de eventos simples y compuestos
108
•
•
108
109
110
112
112
115
117
118
•
•
•
•
vi
Conteo y diagramas de árbol
Multiplicación de opciones
Permutaciones
Factoriales
Combinaciones
Coeficientes binomiales
Espacio muestral
Eventos
Diagramas de Venn-Euler
Propiedad aditiva
Postulados de la probabilidad
Propiedad de la multiplicación
Probabilidad condicional e independencia
Probabilidades y posibilidades
5. Distribuciones de probabilidad
125
5.1. Variable aleatoria discreta y distribuciones de probabilidad
125
•
126
Valor esperado y desviación estándar
5.2. Distribución binomial
132
5.3. Distribución normal
141
•
•
141
145
Modelo de probabilidades continuo
Distribución normal estándar
6. Distribuciones muestrales
161
6.1. Población y muestra
161
Estadística
•
•
Muestreo con o sin reemplazo
Muestra aleatoria simple
161
164
6.2. Parámetros y estadísticos
168
•
•
•
168
168
169
Variabilidad muestral
Distribución muestral de medias
Distribución muestral de proporciones
6.3. Teorema del límite central
173
7. Inferencia estadística
179
7.1. La estimación
179
•
180
Estimación puntual y por intervalos
7.2. Intervalos de confianza para la media y la proporción
183
•
•
Intervalo de confianza para la media poblacional
Intervalo de confianza para una proporción
184
188
7.3. Prueba de hipótesis para la media y la proporción
• Prueba de hipótesis para la proporción
• Muestras grandes
• Muestras pequeñas
191
196
196
197
Respuestas
205
vii
Capítulo 1
1
Introducción
1.1. Estadística
La estadística es la ciencia y el método científico que se ocupa de la recogida y obtención
de datos, de su tratamiento para expresarlos numéricamente y de su análisis para extraer
conclusiones a partir de ellos. Recolectar, organizar, resumir, presentar y analizar datos
son algunas de sus principales funciones. Esta disciplina estudia cuantitativamente los
fenómenos de masa o colectivos, o sea, aquellos fenómenos cuyo estudio sólo puede
efectuarse a través de una colección de observaciones.
La estadística no sólo es útil para el campo de las ciencias, también es una
disciplina que puede ayudarnos en la mayoría de nuestras actividades cotidianas; por
ejemplo, cuando vemos los resultados de alguna elección ciudadana, cuando vamos al
supermercado, cuando recibimos nuestras notas en la escuela, cuando observamos los
resultados de nuestro equipo favorito, cuando vamos al banco o cuando simplemente
queremos saber el estado de nuestras finanzas; en fin, en todo momento estamos en
contacto con ella y por eso, entre muchas otras cosas más complejas que se tratarán en
este libro, es de gran utilidad esta ciencia y todo lo que se deriva de ella.
EJE
M
Ejemplo 1.1.1
Para saber a dónde nos conviene ir al supermercado (para cuidar nuestras finanzas),
tendremos que recopilar datos de diferentes tiendas y así saber cuál nos representa el
menor de los gastos, o cuál es mejor para comprar fruta y en cuál conviene comprar
electrodomésticos. Normalmente ésto lo hacemos mecánicamente, pero existen métodos
matemáticos que resultan muy útiles para obtener resultados precisos.
Ejemplo 1.1.2
Para saber qué candidato es el idóneo y qué probabilidades tiene de ganar en una
contienda electoral; podemos consultar las encuestas y los análisis estadísticos.
1. INTRODUCCION
1
OS
PL
Estadística
Ejemplo 1.1.3
Para saber qué resultados debe obtener nuestro equipo en el fútbol y así poder
llegar a las finales, tendremos que analizar cuántas victorias, empates y derrotas tiene,
cuántos goles a favor y cuántos en contra, así como los datos de sus rivales; esto es
análisis de estadísticas deportivas.
Además de estos usos, la estadística ha sido empleada para engañar a otros. Esto
es posible ya que los métodos de los que se vale pueden ser manipulados para obtener
los resultados que se deseen.
PROBLEMA
Una mala estadística puede resultar del planteamiento de preguntas en forma
incorrecta o de la realización de entrevistas a las personas equivocadas, o de preguntas
en el lugar o momento incorrecto.
SR
ESUELTOS
Ejemplo 1.1.4
Para determinar el sentimiento del público acerca de una nueva ley gubernamental
que está por ponerse en práctica, un entrevistador pregunta a la gente: ¿Cree usted que
deba ponerse en marcha esta injusta ley?
Solución:
El entrevistador manipula su posible respuesta al ponerle el adjetivo de injusta, lo
cual provoca información inútil, si lo que se busca es obtener una opinión imparcial
sobre dicha ley.
Ejemplo 1.1.5
Para pronosticar una elección, un encuestador entrevista solamente a las personas
que salen de un prestigioso centro comercial. ¿Por qué esta situación puede generar
información inútil?
Solución:
Porque es más probable que las personas que salen del centro comercial apoyen
a un candidato en específico por sus condiciones socioeconómicas y ésto no da un
parámetro general de la popularidad del candidato en gente con otro nivel de vida.
2
Capítulo 1
Ejemplo 1.1.6
Para estudiar los patrones de gasto en una compañía de un grupo de ingresos
determinado, se realiza un estudio durante las dos primeras semanas de enero. ¿Por qué
se podría generar información errónea con este método?
Solución:
Los gastos de enero no son típicos durante todo el año, por lo que este estudio
estadístico arrojaría datos irreales sobre los patrones de gasto de la compañía.
EJER
EJERCICIOS 1.1
1.1.1. Explica por qué cada uno de los siguientes estudios quizá no genere la información
deseada:
a) Para determinar el ingreso promedio anual de sus habitantes, el departamento
gubernamental correspondiente de una ciudad creó un cuestionario para ser
contestado vía telefónica por los ciudadanos, marcando números al azar.
b) Para pronosticar qué equipo de fútbol mexicano será el campeón, un encuestador
entrevista a las personas que salen de dos estadios de la Ciudad de México.
c) Para determinar cuántos productos se rompen y se pierden anualmente en una
tienda de abarrotes, y así poder pronosticar y contemplar el riesgo de sus pérdidas,
se decide contar todos los domingos a la hora de abrir los productos en existencia
y cotejarlos con los contados a la hora de cerrar.
1.1.2. Para determinar si un secretario de una institución gubernamental debe seguir en
su cargo, un encuestador pregunta: ¿Piensa usted que este secretario derrochador
debería continuar en su cargo? Explica por qué esta pregunta quizá no obtendrá
la información deseada.
1.1.3. Para determinar qué sabor de refresco es el más vendido, un encuestador recorre todas
las mañanas diferentes rutas sin repetir visita en caso de que nadie se encuentre en casa.
¿Por qué este procedimiento puede generar información equivocada?
1. INTRODUCCION
3
CIC
IOS
Estadística
1.1.4. Para saber si los aficionados de un equipo de baseball están de acuerdo con el
trabajo de la directiva y del entrenador, una revista de deportes pregunta: “¿Está
usted de acuerdo con el trabajo del entrenador de su equipo a pesar de que
juegan muy mal?”.
¿La información obtenida es veraz o manipulada (y por lo tanto errónea)?
1.1.5. Para averiguar si los zapatos que produce una compañía son de buena calidad,
se realiza una encuesta a todos los trabajadores de la compañía. Explique por
qué el planteamiento de este método puede generar información inútil.
1.2. Variable
Una variable es un símbolo, ya sea x, y, z, X, H o B, que puede tomar cualquiera de los
valores de un conjunto predeterminado llamado dominio de la variable. Si la variable
sólo toma un valor, entonces la variable se llama constante.
EJE
M
A una variable que toma cualquier valor entero se le llama variable discreta;
si no es así, se le denomina variable continua, que toma cualquier valor entre dos
valores dados. El número de hijos que cada una de 100 familias tiene es un ejemplo de
datos discretos, mientras que el peso de cada uno de los hijos es un ejemplo de datos
continuos. En general, las mediciones (longitud, peso, tiempo, temperatura, etc.) son
variables continuas, mientras que los valores numéricos que no se pueden fraccionar
son variables discretas (número de habitantes, miembros de una familia o de una
universidad, empleados en una fábrica, número de países, etc.).
Ejemplo 1.2.1
OS
PL
El número (N) de empleados que tiene una compañía sólo puede tomar valores
enteros (1, 2, 3, 4, 5…), por lo tanto, es una variable discreta y el dominio de este conjunto
de valores o datos comprende desde el uno hasta el número total de empleados.
Ejemplo 1.2.2
La altura (A) de los empleados de una fábrica, en donde uno de ellos puede ser
de 1.7, 1.73 ó 1.73481 metros, dependiendo de la exactitud de las mediciones, es una
variable continua; y el dominio de este ejemplo comprende desde el empleado más bajo
de estatura hasta el más alto.
4
Capítulo 1
1.2.1. De los siguientes incisos señala cuáles representan datos discretos y cuáles datos
continuos:
EJER
EJERCICIOS 1.2
a) La estatura de los estudiantes en una universidad.
b) El número de equipos de fútbol que participa en un torneo.
c) La temperatura registrada en una solución química cada minuto.
d) El tiempo de vida de los focos caseros.
e) Los metros que recorre un jugador de fútbol durante un partido de 90 minutos.
f) El número de libros terminados que produce una editorial anualmente.
g) El tamaño de las cajas que compra una compañía para distribuir su producto.
h) La longitud de 3 000 clavos que produce una fábrica al día.
i) El tiempo que se tarda un automóvil en recorrer 10 kilómetros con distintas
condiciones climatológicas.
j) El número de países que firmaron un tratado.
k) El peso de los bebés recién nacidos en un hospital.
1.2.2. De los siguientes incisos, señala cuál es el dominio de las variables y menciona
si son discretas o continuas:
a) El número (N) de litros de leche que produce una vaca al mes.
b) La suma (S) de los puntos obtenidos al lanzar 2 dados.
c) El tiempo (T) que un avión tarda en llegar a 1000 metros de altura.
d) El estado civil de una persona.
1. INTRODUCCION
5
CIC
IOS
Estadística
e) El número (H) de hojas de un árbol.
f) El número (L) de libros completos que se leen en México anualmente.
g) El peso (P) que cargan diariamente unos camiones que van desde 1 hasta
6 toneladas.
h) El número (M) de monedas de 10 pesos que circulan en el mercado.
i) La velocidad (V) de un automóvil en kilómetros por hora.
j) El Estado (E) en México.
k) El diámetro de una esfera.
1.3. Población y muestra
EJE
M
Se le llama población o universo al grupo de datos recolectados que determinan las
características de individuos u objetos. Este grupo de datos puede llegar a ser muy
grande y, por lo tanto, imposible o impráctico de analizar; aquí es cuando se necesita
examinar una pequeña parte del grupo llamada muestra.
OS
PL
Ejemplo 1.3.1
Las alturas y los pesos de los deportistas mexicanos arrojan una gran cantidad de
datos; a todo este grupo de datos se le denomina población; para ahorrarnos tiempo y
trabajo examinamos sólo una parte confiable que genere lo que estamos buscando; a
esta pequeña parte de la población se le denomina muestra.
Cuando una muestra es representativa de una población, de su análisis se pueden
inferir conclusiones importantes acerca de la población; a estas inferencias se les llama
estadística inductiva o inferencial y suelen ser resultado del análisis empírico del
problema; ya que a veces tales inferencias no llegan a ser precisas por completo, se usa
el lenguaje de la probabilidad para sacar conclusiones.
A la parte de la estadística que busca únicamente describir y analizar un grupo
determinado, sin sacar conclusiones, inducciones o inferencias sobre un grupo más
grande, se le conoce como estadística descriptiva o deductiva.
6
Capítulo 1
Ejemplo 1.3.2
Cuando hacemos un análisis de la población por medio de encuestas y/o entrevistas,
y al estudio de los datos se les tiene que interpretar de alguna manera para cotejarlos
con otros, se le llama estadística inductiva o inferencial (como las encuestas televisivas
sobre política y deportes); en cambio, si sólo queremos sacar respuestas concretas, sin
sacar conclusiones o inferencias sobre la población y nos concentramos solamente en
los números arrojados, entonces se les llama estadística descriptiva o deductiva.
EJER
EJERCICIOS 1.3
1.3.1. De los siguientes métodos para recopilar datos y analizarlos, menciona cuál es
estadística descriptiva y cuál, estadística inductiva:
a) Se realiza una encuesta telefónica para saber las tendencias políticas de la población.
b) Se miden y pesan las plantas en un laboratorio para determinar en qué condiciones
viven mejor y calcular su crecimiento.
c) Para determinar cuántas latas de atún tienen algún desperfecto, se analiza
diariamente una de cada 10 latas.
d) Durante las transmisiones de los partidos de fútbol, los cronistas hacen
preguntas sobre qué equipo es considerado el mejor para qué los aficionados
voten por teléfono.
e) Para determinar las condiciones socioeconómicas de los países y poder
compararlos, se hace una encuesta en cada país y se pregunta a la gente sobre su
nivel de vida, para luego interpretar y cotejar las respuestas.
f) El centro de nutrición analiza datos obtenidos al recopilar el peso de todos los habitantes
de la ciudad para conocer el porcentaje de obesidad que existe en la población.
1.4. Azar y probabilidad
La estadística se ocupa del azar por medio de las diversas teorías de probabilidad. El
cálculo de probabilidades nos da leyes de un sistema que se puede clasificar aleatorio,
1. INTRODUCCION
7
CIC
IOS
Estadística
por lo que de alguna manera es un cálculo determinista y por tanto se opone al azar;
mientras que éstas se refieren al determinismo de objetos individuales, las probabilidades
se refieren al determinismo de conjuntos; sin embargo, la probabilidad es la posibilidad
de que algo pueda ocurrir y modera los fenómenos aleatorios, como por ejemplo, lanzar
un dado o una moneda.
Dicho de otra manera, la probabilidad es la característica de un suceso del que
existen razones para creer que se realizará. Los sucesos tienden a ser una frecuencia
relativa del número de veces que se realiza el experimento.
Fenómenos deterministas y aleatorios
EJE
M
A los resultados que pueden ocurrir en un experimento o fenómeno se les llama
eventos. Hay dos tipos de fenómenos: deterministas y aleatorios. En los primeros existe
una relación causa-efecto, es decir, el resultado es predecible de antemano; mientras
que en los fenómenos aleatorios no existe esta relación; podemos conocer de antemano
todos los posibles resultados, pero no podemos predecir con antelación el resultado de
una realización concreta.
OS
PL
Ejemplo 1.4.1
Supongamos que disponemos de un dado regular con todas las caras pintadas de blanco
y en cada una de ellas un número, que van de 1 a 6 sin repetir ninguno.
Definamos los dos experimentos siguientes:
Experimento 1: Tirar el dado y anotar el color de la cara resultante.
Experimento 2: Tirar el dado y anotar el número de la cara resultante.
¿Qué diferencia fundamental observamos entre ambos experimentos?
En el experimento 1, el resultado es obvio: saldrá una cara de color blanco. Es decir,
es posible predecir el resultado. Se trata de un experimento o fenómeno determinista.
En cambio, en el experimento 2 no podemos predecir cuál será el valor resultante.
El resultado puede ser: 1, 2, 3, 4, 5 ó 6. En este caso se trata de un experimento o
fenómeno aleatorio.
8
Capítulo 1
Ejemplo 1.4.2
Un experimento de caída de un cuerpo con velocidad inicial nula es un fenómeno
determinista ya que consiste en un movimiento rectilíneo uniformemente acelerado.
Mientras que la señal recibida en un receptor de un sistema de comunicación, la
evidencia que aportan la pruebas de ADN en un juicio o el hecho de que una persona
herede una enfermedad de sus ascendientes son fenómenos aleatorios.
1.4.1. Si se lanza una pelota hacia arriba repetidas veces con el fin de saber si todas
las veces caerá, ¿es un fenómeno o experimento determinista o aleatorio?
EJER
EJERCICIOS 1.4
1.4.2. Si se deja un trozo de hielo en el agua con el fin de saber si se derretirá, ¿es un
fenómeno determinista o aleatorio?
1.4.3. Lanzar una moneda determinado número de veces para predecir si cae águila o
sol, ¿es un fenómeno determinista o aleatorio?
1.4.4. El nombre del próximo mes, ¿es un fenómeno determinista o aleatorio?
1.4.5. Analizar los números de la lotería, con el fin de calcular el próximo número
ganador, ¿es un fenómeno determinista o aleatorio?
1.4.6. Determina cuál de los siguientes fenómenos es, determinista o aleatorio:
a) Al lanzar dos dados.
b) Poner agua al fuego y comprobar si se evaporará.
c) El marcador del próximo juego de la selección mexicana de fútbol.
d) La fecha de tu cumpleaños.
e) La velocidad de la luz.
f) Los ganadores de los próximos juegos olímpicos.
g) El peso de una persona con respecto de su estatura.
h) Predecir cuándo y cuánto lloverá.
i) La temperatura de congelación del agua a nivel del mar.
1. INTRODUCCION
9
CIC
IOS
Capítulo 2
2
Estadística descriptiva
2.1. Recopilación de datos
Las informaciones numéricas recolectadas en cualquier campo o proceso, cantidad,
magnitud o relación conocida se denominan datos. La organización y la presentación
es una de las primeras tareas para comprender un problema. Un ejemplo es el conjunto
de las estaturas de 100 estudiantes, obtenidas del registro de una escuela; si están
ordenados alfabéticamente sólo son datos sueltos; para comprenderlos numéricamente
es necesaria su ordenación en sentido creciente o decreciente de magnitud. A la
diferencia entre el número mayor y el menor se le conoce como rango de los datos. Si
la estatura mayor de los 100 estudiantes es de 2 metros y la menor es de 1.50, entonces
el rango es 2.0 – 1.50 = 0.50 metros.
Cuando se reúnen grandes cantidades de datos, es útil distribuirlos en clases,
categorías o intervalos, y determinar el número de individuos que pertenecen a cada
categoría; a ésto se le conoce como frecuencia de clase. La tabla 2.1.1 es una distribución
de frecuencias de las estaturas de 100 estudiantes de una escuela.
EJE
M
Ejemplo 2.1.1
Tabla de distribución de frecuencias 2.1.1
Estaturas de 100 estudiantes de una escuela:
Estatura (centímetros)
Número de estudiantes
150 – 154
2
155 – 159
6
160 – 164
18
165 – 169
20
170 – 174
17
175 – 179
24
180 – 184
6
185 – 189
4
190 – 194
2
195 – 199
0
200 – 204
1
TOTAL 100
2. ESTADÍSTICA DESCRIPTIVA
11
OS
PL
Estadística
La primera clase, por ejemplo, comprende las estaturas entre 150 y 154 (de 149.5
hasta 154.5) centímetros y se indica con el rango 150 – 154. La frecuencia de clase es
2, que es el número de estudiantes en esa clase, donde 150 es el límite inferior de clase
y 154 es el límite superior de clase. El intervalo de clase es 5 ya que comprende desde
el 149.5 hasta el 154.5 (154.5-149.5 = 5) y se les denomina fronteras de clase, inferior y
superior respectivamente. La marca de clase es el punto medio de la clase y se obtiene
promediando los límites inferior y superior de clase, por lo tanto, la marca de clase del
]
g
intervalo 150 – 154 es 150 + 154 = 152
2
Si seguimos teniendo información extensa y difícil de analizar, podríamos aumentar
el intervalo de la clase, a lo que se le llama también amplitud, tamaño o longitud de
clase; por ejemplo la tabla 2.1.2.
Ejemplo 2.1.2
Tabla de distribución de frecuencias 2.1.2
Estatura (centímetros)
Número de estudiantes
150 – 159
8
160 – 169
38
170 – 179
41
180 – 189
10
190 – 199
2
200 – 209
1
TOTAL 100
Cuando los datos se agrupan por tamaños (centímetros, litros, toneladas, grados,
números, etc.) como las anteriores tablas de distribución de frecuencias (2.1.1 y 2.1.2),
se les llama distribución numérica o cuantitativa.
PROBLEMA
Para convertir una distribución en una distribución porcentual, habrá que dividir
cada frecuencia de clase entre el número total de factores agrupados y multiplicarlo
luego por 100, como se muestra en el siguiente ejemplo:
SR
ESUELTOS
Ejemplo 2.1.3
De la tabla 2.1.2, convertir las estaturas de los 100 estudiantes de la escuela en una
distribución porcentual.
12
Capítulo 2
Solución:
La primera clase contiene (8/100) x 100 = 8% de datos; la segunda clase comprende
(38/100) x 100 = 38%; la tercera clase (41/100) x 100 = 41%; la cuarta clase (10/100)
x 100 = 10%; la quinta clase (2/100) x 100 = 2%; y la sexta clase (1/100) x 100 = 1%
de los datos. Representado en la tabla, queda como sigue:
Tabla de distribución porcentual 2.1.3
Estatura (centímetros)
Porcentaje (%)
150 – 159
8
160 – 169
38
170 – 179
41
180 – 189
10
190 – 199
2
200 - 209
1
TOTAL 100
Toma en cuenta que en este caso el número de estudiantes es 100, por lo que el
porcentaje queda igual que el número de estudiantes; sin embargo, el total de datos
varía según el análisis y la cantidad de datos que recopilemos o tengamos.
Ejemplo 2.1.4
Convierte la siguiente tabla de distribución de consumo de gas por departamento
en un condominio, en una distribución porcentual.
Tabla de distribución de frecuencias 2.1.4
Número de departamentos
Consumo de gas (litros)
1–5
6
6 – 10
17
11 – 15
10
16 – 20
33
20 - 25
24
TOTAL 90
2. ESTADÍSTICA DESCRIPTIVA
13
Estadística
Solución:
La primera clase contiene (6/90) x 100 = 6.66%; la segunda (17/90) x 100 = 18.88%;
la tercera (10/90) x 100 = 11.11%; la cuarta (33/90) x 100 = 36.66%; y la quinta clase
(24/90) x 100 = 26.66; y queda como sigue:
Tabla de distribución porcentual 2.1.5
Número de departamentos
Porcentaje de litros de gas
1–5
6.66%
6 – 10
18.88%
11 – 15
11.11%
16 – 20
36.66%
20 – 25
26.66%
TOTAL 100%
Otra forma de modificar una distribución de frecuencias es convirtiéndola en una
distribución acumulativa de “menos de” o “más de”. Para poder elaborar una distribución
acumulativa debemos sumar las frecuencias de clase que aparecen en la tabla; para esto,
se tiene que iniciar con la distribución inferior o superior. También es posible crear una
tabla de distribución porcentual acumulativa; en este caso, el procedimiento consiste en
sumar los porcentajes obtenidos en lugar de las frecuencias.
Ejemplo 2.1.5
Convierte la tabla de distribución de frecuencias 2.1.2 en una tabla de
distribución acumulativa.
Solución:
Dado que ninguno de los valores es de menos de 150, 8 de los valores son de menos
de 160; 8+38 = 46 de los valores son de menos de 170; 46+41 = 87 de los valores son
de menos de 180; 87+10 = 97 de los valores son de menos de 190; 97+2 = 99 de los
valores son de menos de 200; y 99+1 = 100 de los valores son de menos de 210; de este
modo es como se obtuvieron los resultados de la tabla de distribución acumulativa que
aparece a continuación:
14
Capítulo 2
Tabla de distribución acumulativa 2.1.6
Estatura (centímetros)
Frecuencia acumulativa
Menos de 150
0
Menos de 160
8
Menos de 170
46
Menos de 180
87
Menos de 190
97
Menos de 200
99
Menos de 210
100
Si se agrupan los datos en categorías no numéricas, la tabla resultante se conoce como
una distribución categórica o cualitativa; sin embargo, las que llaman primordialmente
nuestro interés en este capítulo serán las distribuciones numéricas; la siguiente tabla de
distribución cualitativa sobre las quejas a la compañía de teléfonos es un ejemplo.
EJE
M
Ejemplo 2.1.6
Tabla de distribución cualitativa 2.1.7
Tipo de queja
Número de quejas
Se cortan frecuentemente las llamadas
517
No entran ni salen llamadas de larga distancia
320
Llamadas no reconocidas
El servicio de Internet se suspende
temporalmente
Los servicios tienen un costo muy elevado
1 412
946
2 080
Se cruzan las llamadas
242
Ruido y mala recepción
404
TOTAL 5 921
Nota: En los casos de distribución cualitativa, la clase se determina con anterioridad
y se comparan los datos que tienen algo en común.
2. ESTADÍSTICA DESCRIPTIVA
15
OS
PL
Estadística
EJER
EJERCICIOS 2.1
CIC
2.1.1. Escribe los números 24, 32, 47, 18, 26, 45, 36, 32, 16 y 49 en una lista ordenada
e indica cuál es el rango de este conjunto.
IOS
2.1.2. Escribe los números 127, 142, 136, 143, 122, 118, 147, 127, 115, 138, 149, 116,
125, 141, 136 en orden creciente de magnitud e indica cuál es el rango de este
conjunto.
2.1.3. Elabora una tabla de distribución de las siguientes cantidades de plomo (en
toneladas) emitidas por una fábrica en 70 días, distribuidas en 8 clases, donde la
primera clase es 10 – 13.9 y la última es 38 – 41.9.
20.4
10.4
17.5
19.4
23.5
15.9
10.9
36.1
17.8
24.8
14.4
18.4
30.2
13.3
38.2
19.0
26.1
21.9
24.1
24.4
18.9
14.0
24.6
20.9
15.9
38.0
26.9
17.5
24.6
34.2
28.6
16.2
24.2
19.9
31.8
31.8
36.8
16.7
11.8
30.5
23.0
19.2
32.4
12.9
19.0
19.2
26.8
31.4
11.8
22.7
11.7
28.5
25.7
18.5
23.1
13.3
32.7
11.2
20.1
31.2
22.7
29.6
27.5
35.0
30.6
24.6
20.0
15.8
10.6
14.4
2.1.4. Obtén las marcas de clase y el intervalo de clase de la distribución de los datos
de emisión de plomo.
2.1.5. Convierte la tabla de distribución que obtuviste de los datos de emisión de plomo
en una distribución porcentual.
2.1.6. Convierte la tabla de distribución que obtuviste de los datos de emisión de plomo
en una distribución acumulativa de “menos de”.
2.1.7. Convierte la tabla de distribución que obtuviste de los datos de emisión de plomo
en una distribución acumulativa de “más de”.
2.1.8. En la siguiente tabla, se encuentran las calificaciones finales en química de
120 estudiantes:
16
Capítulo 2
78
69
73
86
72
96
99
86
72
82
61
84
93
75
71
88
93
75
71
74
89
92
74
71
93
60
74
71
93
99
77
72
63
96
83
78
63
96
83
91
91
78
75
76
67
73
75
76
67
80
99
69
70
87
89
86
70
87
89
62
64
92
82
65
80
90
82
65
80
91
88
98
62
82
66
93
62
82
66
88
82
78
67
88
74
84
67
88
74
65
90
87
79
70
83
99
79
70
83
77
75
96
90
89
85
63
90
89
85
60
80
66
98
62
91
72
98
62
91
75
Con estos 120 datos, elabora una tabla de distribución de 8 clases y encuentra lo
que se señala a continuación:
a) La calificación más baja.
b) La calificación más alta.
c) El rango.
d) El límite inferior de la primera clase.
e) El límite superior de la primera clase.
f) La frontera inferior de la segunda clase.
g) La frontera superior de la segunda clase.
h) El intervalo de clase.
i) Las marcas de clase.
j) Las cinco calificaciones más altas.
k) Las cinco calificaciones más bajas.
l) El número de estudiantes con calificaciones de 80 o más.
m) El número de estudiantes con calificaciones de 75 o menos.
n) El porcentaje de alumnos con calificaciones de 85 o más.
2. ESTADÍSTICA DESCRIPTIVA
17
Estadística
2.1.9. Al realizar la tabla de frecuencias anterior (2.1.6) un estudiante agrupa los datos
con los intervalos de clase 60 – 65, 65 – 70, 70 – 75, 75 – 80, 80 – 85, 85 – 90,
90 – 95 y 95 – 100; ¿por qué esta elección de intervalos puede ser incorrecta?
2.1.10. Con los siguientes datos de crecimiento (en centímetros) de 120 plantas en
distintas condiciones de tierra y nutrientes, haga una tabla de distribución que
tenga las marcas 4.995, 14.995, 24.995, 34.995, 44.995, 54.995, 64.995, 74.995,
84.995, 94.995 y 104.995
47.3
65.82
70.11
42.6
47.84
63.63
23.5
83.47
33.77
45.18
75.1
97.49
60.3
17.17
10.85
73.06
20.01
19.89
71.94
88.95
37.13
3.69
84.52
56.89
51.73
81.73
84.15
88.11
28.61
53.99
71.3
36.83
12.19
7.96
67.25
17.06
83.31
83.44
4.13
37.17
28.76
3.1
82.64
79.43
27.21
72.09
7.13
91.58
12.21
37.06
7.61
21.12
66.01
46.83
16.64
53.76
18.94
20.44
57.91
77.09
36.02
15.68
88.26
47
27.25
23.46
35.77
2.21
21.01
80.75
6.97
5.31
58.85
85.78
44.74
71.72
18.21
61.17
44.54
94.66
67.39
40.25
64.18
99.72
27.56
69.22
29.53
42.51
90.21
59.86
29.43
6.08
36.97
74.18
6.2
28.67
14.29
91.6
57.52
89.62
43.37
94.29
99.36
21.16
86.77
35.12
23.03
68.5
42.01
13.46
40.92
27.09
79.97
3.7
97.52
13.25
56.56
74.73
24.95
91.16
2.1.11. Con la tabla de distribución que obtuviste en el ejercicio 2.1.7, determina:
a) El número de plantas menores que 50 cm.
b) El número de plantas mayores que 80 cm.
c) El límite inferior de la sexta clase.
d) El límite superior a la quinta clase.
e) El límite inferior a la décima clase.
18
Capítulo 2
f) El límite superior a la segunda clase.
g) El rango de la distribución.
h) Las fronteras de clase del quinto intervalo.
i) La frontera superior del noveno intervalo.
j) El número de plantas que creció más de un metro.
2.1.12. Convierte la tabla de distribución que obtuviste en el ejercicio 2.1.7, en una tabla
de distribución porcentual y determina:
a) ¿Qué porcentaje de plantas crecieron más de medio metro?
b) ¿Qué porcentaje de plantas no llegó a crecer ni 30 cm?
c) ¿Qué porcentaje de plantas creció entre 40 y 80 cm?
d) ¿Qué porcentaje de plantas creció menos de un metro?
e) ¿Qué porcentaje de plantas creció más de 90 cm?
2.1.13. La siguiente tabla muestra una distribución de frecuencias de los salarios
quincenales de una compañía. De acuerdo con la tabla, determina:
Salarios (pesos)
Número de empleados
2 500 - 2 599
28
2 600 - 2 699
20
2 700 - 2 799
36
2 800 - 2 899
34
2 900 - 2 999
25
3 000 - 3 099
30
3 010 - 3 199
12
TOTAL 185
2. ESTADÍSTICA DESCRIPTIVA
19
Estadística
a) El límite inferior de la segunda clase.
b) El límite superior de la segunda clase.
c) La frontera inferior de la quinta clase.
d) La frontera superior de la quinta clase.
e) El intervalo de clase.
f) Las marca de clase de la cuarta clase.
g) La frecuencia de la tercera clase.
h) El tamaño del primer intervalo de clase.
i) El porcentaje de empleados con salario de más de 2 600 pero menos de 3 000 pesos.
j) El porcentaje de empleados que ganan menos de 2 800 pesos.
k) El número de empleados que cobra menos de 2 500 pesos.
l) El porcentaje de empleados que cobra 3 000 pesos o más.
2.1.14. Un conjunto de datos consta de 38 observaciones, ¿cuántas clases recomendarías?
2.1.15. Un conjunto de datos consiste en 45 observaciones, desde 0 a 29 pesos. ¿Qué
tamaño del intervalo recomendarías?
2.1.16. Un conjunto de datos consta de 230 observaciones que oscilan desde 235 a 567
pesos. ¿Qué intervalo de clase recomendarías?
2.1.17. Una compañía cuenta con cierto número de distribuciones en el área metropolitana.
El número de productos vendidos en una de las distribuidoras en los últimos 20
días es:
65
98
55
62
79
79
63
73
71
85
70
62
66
80
94
59
51
90
72
56
a) ¿Cuántas clases recomendarías?
20
Capítulo 2
b) ¿Qué intervalo de clase recomendarías?
c) ¿Cuál es el límite inferior que recomendarías para la primera clase?
2.1.18. A partir de la siguiente información sobre los pesos en kilogramos de cada uno
de 80 jugadores de fútbol americano, haz una tabla de distribución de frecuencias si:
a) Hay 10 clases.
b) La frontera inferior de la cuarta clase es = 89.995
c) La frontera superior de la sexta clase es = 119.995
d) El límite inferior de la segunda clase es = 70
e) La frecuencia de la séptima clase es = 6
94.63
106.05
70.79
98.29
99.64
125.36
107.37
87.41
157.36
116.19
157.66
124.25
112.07
146.06
73.4
157.74
140.79
117.97
130.93
98.93
72.42
119.19
149.54
127.55
114.36
108.7
90.63
99.87
60.77
155.79
127.76
82.06
121.28
88.7
82.95
90.32
145.13
109.24
107.68
101.68
95.8
102.46
81.23
79.05
71.75
151.48
88.1
112.27
116.92
103.29
132.84
138.85
75.76
118.7
99.63
140.93
70.28
73.28
145.38
100.56
114.97
63.77
70.73
130.73
60.26
154.32
134.86
96.11
85.83
122.1
69.78
101.98
74.93
74.59
135.02
99.73
134.32
145.69
80.99
106.67
2.1.19. Convierte la tabla de distribución que obtuviste con la información anterior en
una distribución porcentual y determina:
a) ¿Qué porcentaje de jugadores pesa más de 100 kilogramos?
b) ¿Qué porcentaje de jugadores pesa menos de 80 kilogramo?
c) ¿Qué porcentaje de jugadores pesa más de 80 kilogramos, pero menos de 100?
d) ¿Qué porcentaje de jugadores pesa menos de 70 kilogramos?
e) ¿Qué porcentaje de jugadores pesa más de 150 kilogramos?
f) ¿Qué porcentaje de jugadores pesa más de 100 kilogramos, pero menos de 150?
2. ESTADÍSTICA DESCRIPTIVA
21
Estadística
2.1.20. Recopila datos sobre las edades de los hermanos de 20 de tus compañeros y haz
una tabla de distribución de frecuencias cuantitativa y una tabla de distribución
porcentual. Determina también qué materias son las favoritas de tus 20
compañeros y realiza con la información obtenida una tabla de distribución
cualitativa.
2.2. Representaciones gráficas
Las distribuciones de frecuencias se usan para condensar conjuntos de datos y dar
una apreciación más fácil del análisis; sin embargo, los datos aún pueden ser más
fáciles de asimilar y por lo general la mejor manera de presentarlos es gráficamente.
A continuación, algunos ejemplos de las representaciones gráficas más útiles y por lo
tanto más comunes.
El siguiente grupo de datos está basado en las edades de 60 trabajadores de una
empresa de colocación de empleados; en esta ocasión, lo usaremos para ejemplificar las
representaciones gráficas.
25
28
31
44
21
41
34
30
31
40
39
28
26
59
42
29
36
36
36
23
46
50
23
57
35
34
38
42
50
47
24
36
50
38
44
30
42
52
39
29
30
33
54
55
40
30
32
40
Tabla de distribución de frecuencias 2.2.1
Edades
Frecuencia
20 – 24
4
25 – 29
9
30 – 34
13
35 – 39
12
40 – 44
9
45 – 49
3
50 – 54
6
55 – 59
4
TOTAL 60
22
33
26
33
32
36
55
51
27
35
29
36
46
Capítulo 2
Histogramas
En cuanto a las distribuciones de frecuencias, la forma de representación gráfica
más común es el histograma. Los histogramas representan las medidas u observaciones
agrupadas en una escala horizontal y las frecuencias de clase en una escala vertical por
medio de rectángulos cuyas bases equivalen a los intervalos de clase y cuyas alturas
corresponden a las frecuencias de clase, por lo que es imposible diseñar histogramas
para distribuciones con clases abiertas.
Histograma de la distribución de edades
14
12
10
8
6
4
2
0
20-24 25-29 30-34
35-39 40-44
45-49 50-54
55-59
Gráficas de barras
Las gráficas de barras son similares a los histogramas; las alturas de los rectángulos
o barras representan las frecuencias de la clase como un histograma pero no hay motivo
para tener una escala horizontal continua.
Gráfica de barras
13
12
9
9
6
4
4
3
20-24
15-29
30-34
35-39
40-44
45-49
50-54
55-59
Edades
2. ESTADÍSTICA DESCRIPTIVA
23
Estadística
Polígono de frecuencias
Los polígonos de frecuencias son menos comunes que los histogramas y las
gráficas de barras, sin embargo, dan una buena impresión general del conjunto de datos
utilizando las “marcas de clase” de cada intervalo como puntos informativos unidos por
una línea. Para convertir un histograma en un polígono de frecuencias sólo es necesario
añadir los puntos medios o marcas de clase y unirlos, agregando en ambos extremos
clases con marcas de clase 0 para sujetar la gráfica a la escala horizontal.
Polígono de frecuencias
14
12
10
8
6
4
2 0
17
22
27
32
37
42
Edades
47
52
57
62
Ejemplo:
Ojivas
Las ojivas son otra forma de representación gráfica que suele ser utilizada como
técnica para representar una distribución acumulativa, en donde los valores son de “menos
de” o “más de”; donde las frecuencias acumulativas se trazan en las fronteras de clase.
Ejemplo:
Transformamos la tabla de frecuencias 2.2.1 en una tabla de frecuencias acumulativa
de “menos de”, para poder hacer la ojiva, y nos queda como sigue:
Tabla de frecuencias acumulativa 2.2.2
24
Edades
Frecuencia acumulativa
Menos de 20
Menos de 25
Menos de 30
Menos de 35
Menos de 40
Menos de 45
Menos de 50
Menos de 55
Menos de 60
0
4
13
26
38
47
50
56
60
Capítulo 2
Ojiva de distribución acumulativa
19.5
24.5
29.5
34.5 39.5
44.5
Edades (fronteras)
49.5
54.5
59.5
Gráficas circulares
Por lo regular, las distribuciones cualitativas se representan gráficamente como
gráficas circulares; en éstas se divide un círculo en secciones, segmentos o partes, que
son proporcionales en tamaño con las frecuencias o los porcentajes correspondientes.
Para elaborar una gráfica circular, primero convertimos la distribución en
una distribución porcentual. Luego, ya que un círculo completo corresponde a 360
grados, obtenemos los ángulos centrales de las secciones necesarias multiplicando los
porcentajes por 3.6.
Ejemplo:
Transformamos la tabla de frecuencias 2.2.1 en una tabla de frecuencias Porcentual
para poder hacer la gráfica circular, y nos queda como sigue:
Tabla de frecuencias porcentual 2.2.3
Edades
Porcentaje (%)
20 – 24
6.66
25 – 29
15
30 – 34
21.66
35 – 39
20
40 – 44
15
45 – 49
5
50 – 54
10
55 – 59
6.66
TOTAL 100
2. ESTADÍSTICA DESCRIPTIVA
25
Estadística
Gráfica circular de porcentajes
55-59
20-24
50-54
6.66% 6.66%
45-49
10%
25-29
15%
5%
40-44
15%
21.66%
30-34
20%
35-39
El ejemplo de gráfica circular fue realizado tomando los mismos datos de los ejemplos
anteriores con el fin de facilitar su contenido y aprendizaje; sin embargo, las gráficas
circulares ilustran más cuando se trata de categorías no numéricas, por ejemplo:
Distribución del mercado mundial de petróleo
Canadá 0.8; 2%
Otros 1.5; 4%
Chile 1.0; 3%
Arabia Saudita 9.1; 24%
Algeria 1.8; 5%
México 1.8; 5%
Kuwait 2.4; 7%
Emiratos Árabes 2.4; 7%
Irán 2.4; 7%
Japón 7.9; 21%
Venezuela 2.4; 7%
EJER
Noruega 2.8; 8%
CIC
EJERCICIOS 2.2
IOS
2.2.1. Dada la siguiente tabla de distribución de las calificaciones de 80 estudiantes en
el examen de ingreso de una Universidad, haz un histograma de frecuencias y
una gráfica de barras.
26
Capítulo 2
Calificaciones
Frecuencia
50 – 59
8
60 – 69
19
70 – 79
33
80 – 89
14
90 – 99
6
TOTAL 80
2.2.2. Con la tabla de distribución de frecuencias del ejercicio anterior (2.2.1), obtén las
marcas y traza un polígono de frecuencias.
2.2.3. Con la tabla de distribución de frecuencias del ejercicio 2.2.1, haz una tabla
de distribución acumulativa de “más de”, y obtén las fronteras de clase y traza
una ojiva.
2.2.4. Determina la distribución porcentual de la tabla del ejercicio 2.2.1 y haz una gráfica
circular con los datos obtenidos.
2.2.5. Con la siguiente tabla de distribución sobre el ingreso mensual de una juguetería, haz
un histograma.
Mes
Pesos
Enero
33 000
Febrero
19 000
Marzo
16 500
Abril
37 000
Mayo
12 500
Junio
18 000
Julio
16 700
Agosto
17 300
Septiembre
20 000
Octubre
24 500
Noviembre
29 500
Diciembre
58 000
TOTAL 302 000
2. ESTADÍSTICA DESCRIPTIVA
27
Estadística
2.2.6. Convierte la tabla de distribución del ejercicio 2.2.5 en una tabla de distribución
porcentual, y traza una gráfica circular.
2.2.7. A partir de la siguiente tabla de distribución de la facturación de 200 cuentas de una
tienda departamental, traza una gráfica de barras.
Importe (pesos)
Frecuencia
0.0 – 199.9
22
200 – 399.9
47
400 – 599.9
66
600 – 799.9
35
800 – 999.9
21
1000 – 1199.9
9
TOTAL 200
2.2.8. A partir de la tabla de frecuencias del ejercicio 2.2.7, obtén las marcas de clase y
traza un polígono de frecuencias.
2.2.9. Convierte la tabla del ejercicio 2.2.7 en una distribución acumulativa de “menos
de” y traza una ojiva.
2.2.10. La siguiente tabla porcentual muestra qué medio de transporte usan en la ciudad
para llegar a su trabajo. Elabora una gráfica circular con los datos que aparecen
a continuación.
.
Medios de transporte
Porcentaje (%)
Automóvil particular
56
Transporte público (camiones)
19
Taxis
4
Metro
20
Otro
1
TOTAL 100
28
Capítulo 2
2.3. Medidas de tendencia central
Me
Me dia
dia
na
Mo
da
Mo
Me da
dia
na
Me
dia
Los valores promedio o medios de un conjunto de datos son muy representativos. Como
tales valores suelen estar hacia el centro del conjunto de datos ordenados por magnitud,
se conocen como medidas de tendencia central, entre los cuales se encuentran la media
aritmética o simplemente media, la mediana y la moda.
Las figuras anteriores muestran las posiciones relativas de la media, la mediana
y la moda gráficamente para mostrar su tendencia central para curvas de frecuencia
sesgadas hacia la derecha o hacia la izquierda; si fueran totalmente simétricas, las tres
medidas coincidirían en el mismo punto central.
Media aritmética
La media aritmética o media es en estadística lo que en otras áreas de las matemáticas
se le puede llamar “promedio”, y se define como sigue:
La media de n números es la suma de los mismos divididos entre n.
EJE
M
Ejemplo 2.3.1
Durante los 12 meses del año 2005, se registraron 6, 8, 4, 2, 6, 15, 20, 19, 15, 9, 10
y 6 días con lluvia. Para sacar la media o expresamente el promedio de días lluviosos
por mes en el 2005 se tiene que:
El total para los 12 meses es de: 6+8+4+2+6+15+20+19+15+9+10+8=122 y por lo
tanto la media = 120/12 = 10.
Ejemplo 2.3.2
El gerente de un restaurante, quien desea estudiar cuánta gente ha ido a comer en la
última semana (7 días), encuentra que 42, 36, 52, 70, 83, 128, 140 personas comieron
en su restaurante.
2. ESTADÍSTICA DESCRIPTIVA
29
OS
PL
Estadística
El total de personas que comió en su restaurante es de 42+36+52+70+83+128+140
=551. Ya que 551/7 = 78.7; ésta es la media de personas que comió en el restaurante por día.
En los ejemplos anteriores es fácil obtener la media, sin embargo, cuando calculamos
las medias de muchos conjuntos diferentes de datos simples, es conveniente contar con
una fórmula que siempre se pueda aplicar, por tanto, la media aritmética de un conjunto
de n números x1, x2, x3, ..., xn se denota por x y se define por:
n
Media = x =
x1 + x2 + x3 + ... + xn
=
n
/x
j
j=1
/x
= n
n
donde x j esncualquiera de los n valores x1, x2, x3, ..., xn que toma una variable x, y donde
el símbolo / x j denota la suma de todos los x j desde j=1 hasta j=n o simplemente se
j=1
denota como / x, / xj ó / j x j .
Si los números x1, x2, x3, ..., xn ocurren f1, f2, f3, ..., fk veces, respectivamente (es decir,
con frecuencias f1, f2, f3, ..., fk ), la media aritmética es:
k
f1 x1 + f2 x2 + ... + fk xk
Media = x =
=
f1 + f2 + ... + fk
/ fx
j
j=1
k
/f
j
=
j
/ fx = / fx
n
/f
j=1
donde n = / f es la frecuencia total o el número total de casos.
Ejemplo 2.3.3
Si 5, 8, 6, 2 ocurren con frecuencias 3, 2, 4 y 1, en ese orden, su media
aritmética es:
x=
f1 x1 + f2 x2 + ... + fk xk (3) (5) + (2) (8) + (4) (6) + (1) (2) 15 + 16 + 24 + 2
=
=
= 5.7
3+2+4+1
10
f1 + f2 + ... + fk
Media aritmética ponderada
Si se sustituyen las frecuencias por pesos se le puede considerar lo que se conoce
como media aritmética ponderada. A veces se asocia a los números x1, x2, x3, ..., xk
ciertos factores de peso (o pesos) w1, w2, w3, ..., wk dependiendo de la “influencia”
asignada a cada número.
w1 x1 + w2 x2 + ... + wk xk
=
w1 + w2 + ... + wk
ponderada con pesos w1, w2, w3, ..., wk .
En este caso, x =
30
/ wx
/w
se llama media aritmética
Capítulo 2
Ejemplo 2.3.4
Si el examen final de un curso cuenta tres veces más que una evaluación parcial
y un estudiante obtiene una calificación de 85 en el examen final y 70 y 90 en los dos
parciales, la calificación media es:
/ wx = (1) (70) + (1) (90) + (3) (85) = 70 + 90 + 255 = 83
w x + w x + ... + w x
x = 1 w1 1 + w2 2 2+ ... + wk k k =
1+1+3
5
/w
Ejemplo 2.3.5
La siguiente información sobre el porcentaje de condominios residenciales
habitados por sus propietarios en tres ciudades de Baja California no tiene el mismo
“peso” o “importancia relativa”, considerando que habían 500 000 residencias en Tijuana,
43 000 en Mexicali y 47 000 en Ensenada, queda como sigue:
Porcentaje (%) de condominios
Ciudad
x=
=
habitados por sus propietarios
Tijuana
40.3
Mexicali
56.4
Ensenada
62.1
w1 x1 + w2 x2 + ... + wk xk (500000) (40.3) + (43000) (56.4) + (47000) (62.1)
=
w1 + w2 + ... + wk
500000 + 43000 + 47000
20150000 + 2425200 + 2918700 25493900
= 590000 = 43.21
590000
Media aritmética para datos agrupados
Cuando los datos se presentan en una distribución de frecuencias, todos los valores
que “caen” dentro de un intervalo de clase dado se consideran iguales a la marca de
clase. La fórmula usada anteriormente para la media con frecuencias / fx se puede
n
aplicar para tales datos agrupados, sin embargo, existen métodos más cortos y con
diferentes alcances.
En el siguiente método se interpreta a x como la marca de clase, a f como su
correspondiente frecuencia de clase, a como cualquier marca de clase supuesta y d =
x-a como las desviaciones de x respecto de a.
n
/ fd
x = a+
j=1
n
j
= a+
/ fd
n
2. ESTADÍSTICA DESCRIPTIVA
31
Estadística
Existe un método más corto llamado método de compilación que suele usarse siempre
que todos los intervalos de clase sean del mismo tamaño c; si es así, las desviaciones
d=x-a puede expresarse como cu, donde u serían los números enteros positivos, negativos
o cero, es decir, 0, ! 1, ! 2, ! 3..., y la fórmula queda como sigue:
k
f/ fu p
j
x = a+
j=1
n
j
/ fu
c = a + c n mc
Ejemplo 2.3.6
A partir de la siguiente tabla de distribución sobre el peso (en kg) de 100 atletas en
un maratón, utiliza los tres métodos aprendidos para obtener su peso medio.
a) Método largo: x =
/ fx
n
b) Variación del método corto: x = a +
/ fd
n
/ fu
c) Método corto o método de compilación: x = a + c n m c
Peso (en kilogramos)
Frecuencia (f)
60 – 62
5
63 – 65
18
66 – 68
42
69 – 71
27
72 – 74
8
Total=
/ fx = 100
Solución:
a) Hacemos otra tabla con los datos necesarios y queda como sigue:
Peso (kg)
Marca de clase (x)
Frecuencia ( f )
60 – 62
61
5
305
63 – 65
64
18
1152
66 – 68
67
42
2814
69 – 71
70
27
1890
72 – 74
73
8
584
n = / fx = 100
32
fx
/ fx = 6745
Capítulo 2
Por lo tanto, aplicando la fórmula y sustituyendo los valores:
x=
/ fx = 6745 = 67.45 Por lo tanto, la media de los pesos es de 67.45 kg
n
100
b) Hacemos otra tabla con los datos que necesitaremos donde a es la marca de
clase que elegimos y queda como sigue:
Marca de clase (x)
Desviación (d=x-a)
Frecuencia (f)
fd
61
-6
5
-30
64
-3
18
-54
67
0
42
0
70
3
27
81
73
6
8
48
n = / fx = 100
/ fd = 45
Por lo tanto, aplicando la fórmula y sustituyendo los valores:
x = a+
/ fd = 67 +
n
45
100 = 67.45 kg
c) Hacemos otra tabla con los datos que necesitaremos donde a es la marca de
clase que elegimos, u son los números enteros positivos, negativos o cero y c es el
intervalo de clase, y queda como sigue:
x
u
f
fu
61
-2
5
-10
64
-1
18
-18
67
0
42
0
70
1
27
27
73
2
8
16
n = / fx = 100
/ fu = 45
Por lo tanto, aplicando la fórmula y sustituyendo los valores:
x = a+c
/ fu m c = 67 + b
n
15 l
100 $ 3 = 67.45 kg
Recuerda que los dos últimos métodos sólo nos dan la respuesta correcta si los
intervalos de clase son iguales, de lo contrario tendremos que usar el método largo (a).
2. ESTADÍSTICA DESCRIPTIVA
33
Estadística
Ejemplo 2.3.7
Tomando en cuenta el ejemplo anterior, si por alguna razón particular los intervalos
de clase no son iguales y sólo contamos con la información de la tabla siguiente, habrá
que utilizar el método largo.
Frecuencia (f)
Peso (kilogramos)
60 – 62
5
63 – 65
18
66 – 68
42
69 – 74
35
Total=
/ f = 100
Hacemos la tabla necesaria:
Peso (kg)
Marca de clase (x)
Frecuencia (f)
fx
60 – 62
61
5
305
63 – 65
64
18
1 152
66 – 68
67
42
2 814
69 – 74
71.5
35
2 502.5
n = / f = 100
/ fx = 6773.5
Por lo tanto, aplicando la fórmula y sustituyendo los valores:
x=
/ fx = 6773.5 = 67.735
n
100
Nota que el resultado de las medias no es el mismo debido a que el último ejemplo
es menos exacto que los anteriores, sin embargo, eso dependerá de la información que
tengamos disponible, ya que entre más datos o información, mayor será la exactitud de
nuestro resultado.
Ejemplo 2.3.8
A partir de la tabla utilizada en el ejercicio 2.1.13, calcula el salario quincenal
medio de los 185 empleados de la compañía, usando a) el método largo y b) el método
corto de compilación.
a) Creamos la tabla que nos ayudará a obtener la media con el método largo y queda
como sigue:
34
Capítulo 2
x
f
fx
$2 549.5
28
$71 386
$2 649.5
20
$52 990
$2 749.5
36
$98 982
$2 849.5
34
$96 883
$2 949.5
25
$73 737.5
$3 049.5
30
$91 485
$3 149.5
12
$37 794
/ fx = $523, 257.5
n=185
Aplicamos la fórmula del primer método y sustituimos los valores:
x=
/ fx = $523, 257.5 = $2, 828.42
n
185
b) Creamos la tabla que nos ayudará a obtener la media con el método corto de
compilación y queda como sigue:
x
u
f
fu
$2 549.5
-2
28
-56
$2 649.5
-1
20
-20
$2 749.5
0
36
0
$2 849.5
1
34
34
$2 949.5
2
25
50
$3 049.5
3
30
90
$3 149.5
4
12
48
n=185
/ fu = 146
Aplicamos la fórmula del método de compilación y sustituimos los valores:
/ fu
146
x = a + c n m c = $2, 749.5 + b 185 l $ $100 = $2, 828.42
Como ejemplo, escogiendo otra marca de clase para a, obtenemos que:
2. ESTADÍSTICA DESCRIPTIVA
35
Estadística
x
u
f
fu
$2 549.5
-3
28
-84
$2 649.5
-2
20
-40
$2 749.5
-1
36
-36
$2 849.5
0
34
0
$2 949.5
1
25
25
$3 049.5
2
30
60
$3 149.5
3
12
36
n=185
/ fu =- 39
/ fu
- 39
O bien: x = a + c n m c = $2, 849.5 + b 185 l $ $100 = $2, 828.42
x
u
f
fu
$2 549.5
0
28
0
$2 649.5
1
20
20
$2 749.5
2
36
72
$2 849.5
3
34
102
$2 949.5
4
25
100
$3 049.5
5
30
150
$3 149.5
6
12
72
n=185
/ fu = 516
/ fu
516
x = a + c n m c = $2, 549.5 + b 185 l $ $100 = $2, 828.42
Nota que el resultado siempre será el mismo independientemente del valor de la
marca de clase que le demos a a; sin embargo, cuanto más céntrica se encuentre ésta,
el calculo será mas fácil.
Mediana
La mediana es el valor “central” o “punto medio” de los dos valores centrales de
un conjunto de números ordenados en magnitud y se define como sigue:
36
Capítulo 2
La mediana es el valor del artículo medio cuando n es non y la media de los dos
artículos medios cuando n es par.
Ejemplo 2.3.9
El conjunto de números 2, 3, 3, 4, 5, 7, 7, 7 y 9 tiene mediana 5.
Ejemplo 2.3.10
El conjunto de números 4, 4, 6, 8, 10, 11, 14 y 17 tiene mediana
] 8 + 10 g
=9
2
Ejemplo 2.3.11
Los datos siguientes representan el tiempo que tardan en bañarse 40 personas
encuestadas dentro de un gimnasio; en este caso, la medida más representativa de los
datos medios o centrales es la mediana; observa por qué:
4
7
10
11
4
8
10
12
5
8
10
13
5
8
10
15
5
8
10
15
5
8
10
15
6
8
10
45
6
9
10
50
6
9
10
60
7
10
11
60
Los dos valores intermedios son 10 y la media de los dos valores intermedios es 10.
La media es de 13.325, por lo tanto, la mediana es más representativa de los tiempos
que la media.
Para datos agrupados, la mediana está dada por:
n
- _ / f i1 p
Mediana = L 1 + f 2
c
fmediana
Donde:
L 1 = frontera inferior de la clase que contiene a la mediana
n = número de datos o frecuencia total
_ / f i1 = suma de las frecuencias de las clases inferiores a la clase de la mediana
fmediana = frecuencia de la clase de la mediana
c = tamaño del intervalo de clase de la mediana
2. ESTADÍSTICA DESCRIPTIVA
37
Estadística
PROBLEMA
Ejemplo 2.3.12
SR
A partir de la siguiente tabla utilizada en el ejemplo 2.3.6 obtén la mediana
utilizando la fórmula para la mediana con datos agrupados.
ESUELTOS
Peso (kilogramos)
Frecuencia (f)
60 – 62
5
63 – 65
18
66 – 68
42
69 – 71
27
72 – 74
8
Total= / f = 100
Solución:
Debido a que la suma de las primeras dos frecuencias de clase es 5+18=23 y las
primeras tres frecuencias de clase 5+18+42=65, queda claro que la mediana se encuentra
en la tercera clase, la cual es, por lo tanto, la clase de la mediana. Entonces:
L 1 = frontera inferior de la clase que contiene a la mediana = 65.5
n = número de datos o frecuencia total = 100
_ / f i1 = suma de las frecuencias de las clases inferiores a la clase de la mediana
= 5+18 = 23
fmediana = frecuencia de la clase de la mediana = 42
c = tamaño del intervalo de clase de la mediana = 3
Por lo tanto:
n
100
- _ / f i1 p
- (23) p
f
27
Mediana = L 1 + f 2
c = 65.5 + 2
$ 3 = 65.5 + b l $ 3 = 67.4 kg
fmediana
42
42
Es decir, la mediana es 67.4 kg o 67 en caso de que sólo tengamos datos enteros.
Moda
La moda es una de las medidas de tendencia central y se define simplemente
como el valor que ocurre con la mayor frecuencia y más de una vez en un conjunto de
números. La moda puede no existir e incluso no ser única.
38
Capítulo 2
Ejemplo 2.3.13
EJE
M
El conjunto 3, 3, 6, 8, 10, 10, 10, 11, 11, 13 y 19 tiene moda 9.
Ejemplo 2.3.14
El conjunto 2, 3, 5, 7, 8, 10, 15 y 18 no tiene moda.
Ejemplo 2.3.15
El conjunto 3, 4, 5, 5, 5, 6, 6, 7, 8, 8, 8 y 9 cuenta con dos modas, 5 y 8, y se le
conoce como bimodal.
La distribución con una moda se llama unimodal.
Ejemplo 2.3.16
Se preguntó a veinte personas qué color principal consideran el indicado para
ponerlo en el logotipo de un partido político; las respuestas en orden de aparición
fueron: verde, rojo, verde, azul, amarillo, verde, negro, rojo, blanco, blanco, azul,
verde, verde, rojo, negro, blanco, amarillo, amarillo, rosa y azul. ¿Cuál es la moda o la
selección modal de este conjunto de colores?
Acomodamos los datos:
Colores
Frecuencia
Verde
5
Rojo
3
Azul
3
Amarillo
3
Negro
2
Blanco
3
Rosa
1
TOTAL 20
Por lo tanto, la moda o selección modal es verde.
Como notamos, la moda es la medida de tendencia central que nos funciona para
datos donde el resultado que requerimos es de la mayoría.
2. ESTADÍSTICA DESCRIPTIVA
39
OS
PL
Estadística
En los casos de datos agrupados donde se haya construido una curva de frecuencias
para ajustar los datos, la moda será(n) el(los) valor(es) de x correspondiente(s) al(os)
/
máximo(s) de la curva. Este valor x se denota por x .
La moda llega a obtenerse de una distribución de frecuencias o de un histograma
a partir de esta fórmula:
/
T
Moda = x = L 1 + b T + 1T l c
1
2
Donde:
L 1 = frontera inferior de la clase con mayor frecuencia (clase modal o clase que
contiene a la moda).
T 1 = diferencia de la frecuencia modal con la frecuencia de la clase inferior inmediata.
T 2 = diferencia de la frecuencia modal con la frecuencia de clase superior inmediata.
PROBLEMA
c = tamaño del intervalo de clase modal.
SR
Ejemplo 2.3.17
ESUELTOS
A partir de la tabla de distribución usada en el ejercicio 2.1.13, calcula el salario
modal de los 185 empleados de la compañía.
Salarios (pesos)
Número de empleados
2 500 - 2 599
28
2 600 - 2 699
20
2 700 - 2 799
36
2 800 - 2 899
34
2 900 - 2 999
25
3 000 - 3 099
30
3 010 - 3 199
12
TOTAL 185
Solución:
L 1 = $2 699.5 T 1 = 36-20 = 16 T 2 = 36-34 = 2 c = $100
Por tanto:
T
16
x = L 1 + b T + 1T l c = 2699.5 + b 16 + 2 l $ 100 = $2788.4
1
2
es decir, el salario modal de la distribución anterior es $2 788.4.
/
40
Capítulo 2
EJERCICIOS 2.3
EJER
2.3.1. A partir de los siguientes conjuntos de datos, calcula la media, la mediana y la moda:
a)
b)
c)
d)
e)
1
1
2
3
3
3
4
4
5
5
6
6
6
6
7
8
8
9
9
9
5
7
4
5
2
7
5
6
4
8
6
2
8
9
5
6
6
8
6
3
6
6
7
8
8
8
9
9
10
11
11
11
12
13
14
14
15
15
17
18
19
19
22
22
23
45
32
28
42
33
35
51
49
42
24
24
50
41
24
55
52
25
36
42
107
104
111
112
122
121
119
113
118
103
102
117
106
116
101
105
108
110
114
109
100
120
115
CIC
2.3.2. De un total de 100 números, 20 eran cuatros, 40 eran cincos, 15 eran seises, 10 sietes
y el resto eran ochos. ¿Cuál es la media, la mediana y la moda de estos números?
2.3.3. Las calificaciones finales de un estudiante son: matemáticas 85, química 80,
historia 92 y educación física 76. Si los créditos de las materias son de 5, 5, 7 y 3,
respectivamente, ¿cuál es el promedio apropiado de sus calificaciones?
2.3.4. Una empresa tiene 60 empleados; 40 ganan $100 por hora y 20 ganan $150 por hora.
Determina cuál es la ganancia media por hora.
2.3.5. Un banco tiene 130 empleados; 80 ganan $6 000 al mes, 45 ganan $8 000 al mes y 5
ganan $50 000 mensuales. Obtén la media y la mediana de estos datos y argumenta
cuál es la medida de tendencia central más representativa para el promedio de
ganancias por empleado al mes.
2. ESTADÍSTICA DESCRIPTIVA
41
IOS
Estadística
2.3.6. Seis grupos de estudiantes de 10, 14, 20, 16, 15 y 5 individuos reportaron
pesos medios de 53, 58, 63, 68, 73 y 78 kilos. ¿Cuál es el peso medio de los
estudiantes?
2.3.7. Si el salario anual medio de 3 directivos de una compañía es de $160 000, ¿es posible
que uno de ellos cobre $500 000?
2.3.8. Un elevador soporta 480 kg. Si entraron 8 personas, de los cuales el peso medio de
los 4 hombres es de es de 70 kg, de las 2 mujeres es de 60 kg y de los 2 niños es de
35 kg, ¿está sobrecargado el elevador?
2.3.9. Tres profesores de ciencias sociales, que tienen 32, 25 y 27 alumnos, en ese orden,
reportaron las siguientes medias de calificaciones en sus grupos: 79, 74 y 82. Obtén
la calificación promedio de todos los grupos.
2.3.10. La siguiente tabla de distribución muestra los promedios de las calificaciones finales
aprobatorias de 105 estudiantes de secundaria. ¿Cuál es la media de las calificaciones
por estudiante?
Calificaciones promedio
Número de estudiantes
60
4
65
7
70
12
75
15
80
28
85
19
90
10
95
7
100
3
TOTAL 105
2.3.11. La siguiente tabla de distribución muestra el promedio o marcas de clase del diámetro
(en milímetros) de 1 000 empaques producidos diariamente por una fábrica.
¿Qué promedio de tamaño tienen los empaques producidos en esta fábrica?
42
Capítulo 2
Diámetro (mm)
Número de empaques
93
123
97
167
101
204
105
172
109
111
113
81
117
77
121
53
125
12
TOTAL 1000
2.3.12. Encuentra las medias de las siguientes tablas de distribución:
a) Estaturas de 135 estudiantes de una escuela:
Estatura (cm)
Número de estudiantes
150 – 154
6
155 – 159
10
160 – 164
17
165 – 169
22
170 – 174
32
175 – 179
24
180 – 184
11
185 – 189
8
190 – 194
4
195 – 199
1
TOTAL 135
b) Estaturas de los mismos 135 estudiantes con mayor intervalo de clases:
2. ESTADÍSTICA DESCRIPTIVA
43
Estadística
Estatura (centímetros)
Número de estudiantes
150 – 159
16
160 – 169
39
170 – 179
56
180 – 189
19
190 – 199
5
TOTAL 135
c) Peso de 90 hombres que asisten regularmente a una clínica nutricional.
Peso (kilogramos)
Frecuencia
40 – 49.9
4
50 – 59.9
7
60 – 69.9
20
70 – 79.9
26
80 – 89.9
23
90 – 99.9
8
100 – 109.9
2
TOTAL 90
d) Tiempo que tardan 50 automóviles en llegar a 100 km por hora desde 0 km
por hora acelerando al máximo.
Tiempo (segundos)
Frecuencia
2 – 4.99
4
5 – 7.99
15
8 – 10.99
19
11 – 13.99
9
14 o más.
3
TOTAL 50
e) Salarios mensuales de 163 trabajadores de una fábrica maquiladora de ropa.
¿Expresa tu opinión sobre si la media es representativa en este caso? Toma en
cuenta que los intervalos de clase no son del mismo tamaño.
44
Capítulo 2
Salarios (pesos)
Número de trabajadores (frecuencia)
3 000 – 3 999
38
4 000 – 4 999
51
5 000 – 5 999
19
6 000 – 6 999
22
7 000 – 7 999
12
8 000 – 8 999
8
9 000 – 9 999
5
10 000 – 14 999
6
15 000 – 50 000
2
TOTAL 163
2.3.13. A partir de las tablas de distribución del ejercicio anterior (2.3.12) encuentra la
mediana a), b), c), d) y e), y compara los resultados.
2.3.14. Hipotéticamente, a partir de las tablas de distribución del ejercicio 2.3.12,
encuentra la moda a), b), c), d) y e) usando la fórmula; compara los resultados.
2.3.15. Los siguientes números son las edades de 165 jóvenes adultos menores de 30
años que hacen alguna clase de deporte o ejercicio regularmente. Obtén a) la
media, b) la mediana y c) la moda:
28
25
21
28
21
21
21
28
21
26
29
20
27
21
20
25
27
22
25
20
19
25
24
25
20
19
24
24
23
19
21
24
23
25
24
26
22
19
26
21
21
28
27
23
18
24
18
22
19
26
22
20
23
25
21
28
24
28
27
27
19
19
19
20
24
27
21
20
28
26
20
27
27
29
26
21
19
19
22
28
28
23
25
24
20
22
20
26
22
29
19
26
22
24
23
23
20
29
19
19
25
28
28
26
23
28
21
27
27
28
27
24
27
27
20
27
19
22
20
25
23
26
24
29
22
24
18
23
21
22
20
29
20
22
28
20
23
27
25
19
22
27
19
18
19
23
24
22
24
19
18
25
18
25
25
20
27
21
24
23
22
21
21
24
26
2. ESTADÍSTICA DESCRIPTIVA
45
Estadística
2.3.16. A partir de los siguientes datos en kilogramos obtenidos al pesar el fruto de
200 manzanos que crecen en 6 hectáreas de un rancho agricultor, obtén a) la
media, b) la mediana y c) la moda. Ordénalos, distribúyelos en tablas y obtén los
resultados con las fórmulas para datos agrupados.
153.7
120.2
111.9
96.4
131.6
100.7
202.4
200.6
162.5
147.8
157.9
136.8
138.1
152.6
194.8
194.5
215.7
179.3
78
168.2
211.5
88.5
121.8
79.7
85.8
211.6
82.3
109.2
99.5
157.2
132.6
112.4
165
114.3
90.2
137.8
116.5
102.2
131.4
122.3
81.1
208.7
218.8
86.2
126.3
177
143.1
165.2
112.2
180.4
150.3
122.1
82.1
168.5
142.2
167.8
122.4
114
86.2
217.6
145.5
120.7
150.7
114.3
212.2
219
159.8
165.1
176.4
194.6
107
129.1
121.2
159.3
216.3
107.1
201.9
106.8
121.9
139.7
218.6
87.7
93
124.3
129.4
119.2
128.4
193.3
145.2
195.8
131.8
215.9
155.1
98
214.4
219
110.6
175.2
170
177
150.9
171
203.1
90.8
124.9
173.2
99.7
128.7
202.8
121
181.1
130.7
162
152.9
101.8
219.6
173
209.7
91.2
195.4
132.3
178.5
147.9
84.1
206.2
152.3
126.3
113.7
82.3
129.2
221.3
89.8
97.8
140.8
132.8
139.6
78.1
157.6
174.5
223.1
90.6
146.8
200.5
110.1
92.8
223.4
161.7
209.6
221.4
179.1
119.3
108
104.2
210.3
81.7
126.3
114
199.1
131.3
83.6
216.7
168.2
88.7
92.6
179.4
194.5
157.4
171.3
192.5
77.8
99.2
183.5
176.9
136.2
177.4
93.9
214.3
188.6
110.4
172.5
183.6
199.7
105.9
107.8
193.6
112.4
212.8
196.9
126.5
174.2
196.3
135.6
116.1
191.5
134.9
103.1
196
125.5
216.4
102.3
2.3.17. A partir de los siguientes datos obtenidos al cronometrar el tiempo en minutos
de 300 automovilistas que recorren la autopista México - Cuernavaca, obtén
a) la media, b) la mediana y c) la moda. Ordénalos, distribúyelos en tablas y
obtén los resultados con las fórmulas para datos agrupados.
46
Capítulo 2
52
46
50
54
46
47
51
46
46
53
56
57
48
46
47
51
46
51
54
47
46
48
53
56
52
51
51
51
55
51
49
51
49
55
56
54
52
52
56
45
48
56
52
56
50
49
47
40
52
55
49
45
46
53
50
54
54
56
55
57
48
47
55
49
50
54
50
55
46
56
51
54
50
52
55
46
53
53
50
54
49
49
56
54
50
53
48
46
59
62
47
54
48
56
49
55
55
51
52
52
55
38
55
55
57
45
49
61
56
50
46
55
40
51
51
55
56
55
52
47
55
57
52
46
50
51
54
55
51
54
49
47
46
56
57
50
48
46
51
51
33
47
54
57
49
49
50
46
55
49
46
56
52
52
56
49
55
51
56
48
46
50
56
49
47
49
52
57
56
53
47
52
48
51
45
50
52
60
48
57
48
54
48
49
47
47
65
47
54
54
49
46
50
48
53
47
52
56
49
48
57
51
52
52
56
45
52
54
60
48
48
56
55
55
46
49
53
59
53
46
54
48
65
48
53
56
53
56
45
47
56
57
47
52
56
54
53
53
46
55
56
46
53
48
50
51
53
41
50
46
48
46
46
51
52
50
46
56
49
46
53
49
46
56
54
49
53
53
49
53
51
50
55
53
48
53
45
55
45
60
55
50
53
48
54
46
51
57
45
45
63
53
52
49
49
56
51
49
50
48
2. ESTADÍSTICA DESCRIPTIVA
47
Estadística
2.3.18. A partir de los siguientes datos obtenidos al medir el diámetro en centímetros
de 350 perlas en un criadero, obtén a) la media, b) la mediana y c) la moda.
Ordénalos, distribúyelos en tablas y obtén los resultados con las fórmulas para
datos agrupados.
48
0.9753
0.9796
1.0088
0.6552
1.1266
1.0666
0.6488
0.9018
1.1126
1.0436
0.8066
1.322
1.3898
1.2216
0.7242
1.3526
0.9064
1.3027
1.1125
0.8958
0.7443
1.2446
0.9833
1.3902
0.6105
1.2913
1.1167
0.5514
0.7011
1.0445
0.7185
1.4625
1.4748
1.1591
0.9155
0.5867
1.4582
1.353
0.5994
0.5555
1.1357
0.8678
0.7461
1.0303
0.8344
1.0702
1.4316
0.6439
1.4652
0.6362
1.3869
0.6154
0.8344
1.4093
0.8428
1.1477
1.2745
1.2347
1.3921
1.0682
1.0106
1.4584
1.3572
1.0905
1.321
1.3618
0.8932
0.7303
1.3281
1.0981
1.2925
1.4953
1.241
1.4023
1.1793
1.3228
1.1142
1.3462
1.3837
1.1348
0.6371
1.0004
1.2374
1.2703
0.6937
1.3913
1.409
0.6206
0.7793
0.5883
0.6657
1.2956
0.9042
0.7436
0.8264
1.4372
0.7195
1.048
1.0251
1.4061
0.9674
0.5865
0.5235
1.2279
0.6751
0.6845
1.3875
0.8165
1.4278
0.9569
0.9537
1.4475
1.0415
0.5807
1.4761
0.5816
1.3194
0.5127
0.7169
0.5002
1.4385
0.725
1.4308
1.3042
0.6951
1.2652
1.1935
0.8962
0.8746
0.8868
0.5074
1.4218
0.5111
0.6418
1.2645
1.1525
0.6321
1.2941
1.1636
0.5189
1.1393
1.0462
1.3656
0.8097
0.574
0.5039
0.9239
0.5084
0.7162
0.8279
0.8998
1.1939
1.4756
1.3415
1.178
0.6069
0.7824
0.762
0.6775
1.0134
1.0101
1.1846
0.7086
1.2884
1.0911
0.8084
0.9502
1.0144
0.5428
0.5578
1.1445
0.7713
0.565
1.3632
1.1852
1.3284
0.9335
0.8587
0.5815
0.5314
1.1202
0.6021
1.3734
1.0434
1.1363
0.9813
1.0039
0.5226
1.1407
1.4209
0.9986
0.9409
0.5961
0.558
0.5273
1.2693
1.2928
1.0701
1.0889
1.0992
1.024
1.4285
0.6173
0.6847
1.2228
1.057
1.0832
0.6162
0.6112
1.0209
0.8391
0.5309
0.6373
1.3952
0.5281
1.0707
1
0.8418
1.3034
0.7391
1.4422
1.0929
1.1193
0.763
1.1939
0.959
0.6004
1.4708
0.9735
0.5932
0.96
1.2835
0.621
0.6206
0.8278
1.3917
0.8684
0.8527
1.159
0.8072
0.9832
1.2625
1.2215
1.2703
0.6436
0.652
0.968
0.5591
1.3184
0.6476
0.5949
0.8853
0.8618
0.8184
1.4093
0.5116
1.4623
0.8144
0.6309
0.9326
1.4497
0.7124
1.4083
0.7118
1.275
0.7377
0.63
1.1439
1.2252
1.2872
0.5998
0.5333
0.6487
0.7396
1.0285
1.1601
0.8402
0.8521
1.0696
1.1245
1.1715
0.7155
1.4101
1.2491
0.633
0.7717
1.0809
0.9041
1.1306
0.7103
0.7419
0.7849
0.715
0.7509
1.3406
1.1659
1.0698
0.7477
0.7109
0.5668
0.9719
1.1505
0.7303
0.7157
0.7251
0.9702
1.1655
0.6304
1.0844
0.5935
1.4847
0.958
1.4765
0.6408
1.2045
0.9381
0.6036
0.9522
1.0294
0.8914
0.8503
1.3341
0.8182
1.298
0.5042
1.4215
1.2538
0.839
1.4085
0.5862
1.1697
1.4458
1.311
0.8618
1.2343
1.3918
0.5694
1.3698
1.3376
0.9061
0.9116
1.1421
1.2353
0.5135
0.8399
0.7849
0.503
0.5503
1.2272
1.1282
Capítulo 2
2.4. Medidas de dispersión y de posición
La dispersión o variación de los datos es el grado en que los datos numéricos tienden a
esparcirse alrededor de un valor promedio. Tomemos como ejemplo a un jugador (A) de
básquetbol que ha anotado 22, 26 y 24 puntos en sus tres primeros juegos, mientras que
un compañero (B) anotó 41, 13 y 18 puntos en los mismos juegos. Ambos jugadores
tienen promedio de 24, sin embargo, el primer jugador es más consistente. Es por ello
que necesitamos valorar el grado en que los datos están dispersos; las medidas que esta
información proporciona se conocen como medidas de variación o de dispersión.
Rango o amplitud
El rango o la amplitud de un conjunto de datos es una de estas medidas de dispersión
y se define como el valor mayor menos el valor menor.
EJE
M
Ejemplo 2.4.1
OS
PL
Para el jugador A del ejemplo anterior, tenemos que la amplitud o el rango es de
26 – 22 = 4, y para el jugador B 41 – 13 = 28.
Ejemplo 2.4.2
La amplitud del rango del conjunto 2, 3, 4, 5, 5, 6, 7, 8, 9, 10 y 12 es 12 – 2 = 10.
A pesar de lo fácil que puede resultar calcular los rangos, ésta no es una medida de
dispersión muy útil en la mayoría de los casos, ya que no nos indica nada acerca de los
valores que caen entre los dos extremos.
Ejemplo 2.4.3
Conjunto 1 = 2, 15, 15, 15, 15, 15, 15, 15.
Conjunto 2 = 2, 2, 2, 2, 15, 15, 15, 15.
Conjunto 3 = 2, 3, 5, 7, 10, 12, 13, 15.
Los tres conjuntos tienen un rango de 15 – 2 = 13, pero la dispersión es totalmente distinta.
Desviación media
Otra medida de dispersión que puede ser más útil que la anterior para distintos
propósitos es la desviación media o desviación promedio.
2. ESTADÍSTICA DESCRIPTIVA
49
Estadística
La desviación media de un conjunto de n números x1, x2, ..., xn se abrevia DM y se
define como:
n
Desviación media (DM) =
/
j=1
xj - x
n
=
/
n
x-x
=
x-x
donde x es la media aritmética de los números y x - x es la desviación de x, respecto
de x (el valor absoluto de un número es el número sin el signo asociado y se indica con
las líneas verticales colocadas a los lados del número; por - 5 = 5 y + 4 = 4 ).
Ejemplo 2.4.4
Calcula la desviación media del conjunto 4, 6, 7, 10, 13.
x=
4 + 6 + 7 + 10 + 13 40
= 4 =8
5
Por lo tanto:
DM =
4 - 8 + 6 - 8 + 7 - 8 + 10 - 8 + 13 - 8
4+2+1+2+5
=
= 2.8
5
5
Si x1, x2, ..., xk ocurren con frecuencias f1, f2, ..., fk respectivamente, la desviación
media puede expresarse:
DM =
/f
j
xj - x
=
n
/f
x-x
= x-x
n
k
PROBLEMA
donde n = / fj = / f . Esta forma es útil para datos agrupados, donde las x j representan
j=1
las marcas de clase y las f son las frecuencias de clase correspondientes.
SR
Ejemplo 2.4.5
ESUELTOS
A partir de la tabla del ejemplo 2.3.6, calcula la desviación media de los pesos de
los atletas.
Solución:
Como vimos en este ejemplo, la media es ] x g = 67.45 kg y creamos la tabla siguiente:
50
Capítulo 2
Peso (kg)
Marca de
Frecuencia
f x-x
clase
] x g = 67.45
60 – 62
61
6.45
5
32.25
63 – 65
64
3.45
18
62.10
66 – 68
67
0.45
42
18.90
69 – 71
70
2.55
27
68.85
72 – 74
73
5.55
8
44.40
(f)
n = / fx = 100
/f
x - x = 226.50
Por lo tanto:
DM =
/f
x-x
226.50
= 100 = 2.26 kg
n
Desviación estándar y varianza
La desviación estándar es por mucho la medida de dispersión más usada y es
un planteamiento alternativo más eficaz que la desviación media, porque consiste en
trabajar con los cuadrados de las desviaciones de la media para evitar las dificultades
teóricas que representan los signos, y sacamos la raíz cuadrada del resultado para
compensar; y queda: / (x - x ) 2
n
Es común que se modifique esta fórmula dividiendo la suma de las desviaciones
cuadráticas de la media entre n-1 en vez de n, por lo tanto, la desviación estándar
de la muestra, que se expresa regularmente con una s (que llamaremos fórmula
corregida) queda:
n
/^
Desviación estándar = s =
xj - x h2
j=1
n-1
/]
=
x - x g2
n-1
y su cuadrado, la varianza de la muestra:
n
/ ^x
Varianza = s 2 =
j
- x h2
j=1
n-1
/ ]x - x g
2
=
n-1
2. ESTADÍSTICA DESCRIPTIVA
51
Estadística
EJE
M
Ejemplo 2.4.6
Obtén la desviación estándar s y la varianza s 2 de los conjuntos:
OS
PL
a) 4, 16, 16, 16, 16, 16.
b) 4, 4, 4, 16, 16, 16.
c) 4, 6, 8, 10, 14, 16.
Solución:
/ x 4 + 16 + 16 + 16 + 16 + 16 = 84 = 14
a) x = n =
6
6
/ ]x - x g
2
s=
n-1
=
(4 - 14) 2 + (16 - 14) 2 + (16 - 14) 2 + (16 - 14) 2 + (16 - 14) 2 + (16 - 14) 2
6-1
=
100 + 4 + 4 + 4 + 4 + 4
=
5
24 = 4.89
s 2 = 4.89 2 = 24
La desviación estándar s del conjunto a es 4.89 y la varianza s 2 es 24.
/ x 4 + 4 + 4 + 16 + 16 + 16 = 60 = 10
b) x = n =
6
6
/ ]x - x g
2
s=
n-1
=
(4 - 10) 2 + (4 - 10) 2 + (4 - 10) 2 + (16 - 10) 2 + (16 - 10) 2 + (16 - 10) 2
6-1
=
36 + 36 + 36 + 36 + 36 + 36
=
5
43.2 = 6.57
s 2 = 6.57 2 = 43.2
La desviación estándar s del conjunto b es 6.57 y la varianza s 2 es 43.2
/x
c) = x = n = 4 + 6 + 8 + 10 + 14 + 16 = 58 = 9.66
6
6
52
Capítulo 2
/ ]x - x g
2
s=
n-1
=
(4 - 9.66) 2 + (6 - 9.66) 2 + (8 - 9.66) 2 + (10 - 9.66) 2 + (14 - 9.66) 2 + (16 - 9.66) 2
6-1
=
32 + 13.4 + 2.75 + 0.11 + 18.83 + 40.19
=
5
21.45 = 4.63
s 2 = 4.63 2 = 21.45
La desviación estándar s del conjunto c es 4.63 y la varianza s 2 es 21.45
Se puede observar que el conjunto c muestra menor dispersión, sin embargo, el
efecto está enmascarado por el hecho de que los valores extremos afectan más a la
desviación estándar y a la varianza que a la desviación media ya que las desviaciones
se elevan al cuadrado.
En los ejemplos anteriores mostramos la definición de una muestra con n-1 ya
que el valor resultante representa un mejor estimado de la desviación estándar; sin
embargo, para los valores grandes de n (de modo preciso n>30), prácticamente no existe
diferencia entre las definiciones, por lo que usaremos la primera fórmula para explicar
a la desviación estándar en caso de tener los datos agrupados o con frecuencias.
/ ]x - x g
/x
2
s=
n
=
2
=
n
] x - x g2
Además, siempre que se necesite el mejor estimado podemos obtenerlo
n
multiplicando el resultado de la fórmula anterior por n - 1 .
Si x1, x2, x3, ..., xk ocurren con frecuencias f1, f2, f3, ..., fk , respectivamente, la desviación
estándar suele expresarse como:
k
/ f ^x
j
j=1
s=
j
n
- x h2
/ f]x - x g
2
=
n
=
/ fx
n
2
=
] x - x g2
Por lo tanto, los datos agrupados se puede expresar de la siguiente forma:
Si d j = x j - a son las desviaciones de x j con respecto de una constante arbitraria a
(como vimos con la media aritmética), encontramos que:
k
/d
s=
j=1
n
2
k
2
j
f/d p
j
-
j=1
n
=
/d
n
2
/d
-c n m =
2
d2 - d 2
o en caso de que ocurran con frecuencias encontramos que:
2. ESTADÍSTICA DESCRIPTIVA
53
Estadística
k
/ fd
j
s=
j=1
2
k
2
j
j
-
n
f/ fd p
j=1
/ fd
j
=
n
2
n
/ fd
-c n m =
2
d2 - d 2
Cuando los datos se encuentran en una distribución de frecuencias, cuyos intervalos
de clase son del mismo tamaño c, se tiene d j = cu o x j = a + cu y el resultado anterior
se convierte en:
k
/ fu
j
s=c
j=1
n
2
k
2
j
f/ fu p
j
-
j=1
n
j
=c
/ fu
2
n
/ fu
- c n m = c u2 - u 2
2
PROBLEMA
Este es el método de codificación utilizado para calcular la desviación estándar y
debe usarse siempre que los intervalos de clase sean iguales, como lo aprendimos con
la media aritmética.
SR
Ejemplo 2.4.7
ESUELTOS
Con los mismos datos de la tabla del ejemplo 2.3.6 obtén la desviación estándar
por medio de:
/ f ] x - x g2
a) Método largo:
n
b) Método intermedio:
/ fd
n
2
/ fd
-c n m
c) Método corto de codificación: c
2
/ fu
n
2
/ fu
-c n m
2
Solución:
a) Sabemos que x = 67.45 kg y se ordena como sigue:
Peso (kg)
Marca de
x-x
clase (x)
= x-67.45
60 – 62
61
-6.45
41.6025
5
208.0125
63 – 65
64
-3.45
11.9025
18
214.245
66 – 68
67
-0.45
0.2025
42
8.5050
69 – 71
70
2.55
6.5025
27
175.5675
72 – 74
73
5.55
30.8025
8
] x - x g2
Frecuencia
(f)
n = / f = 100
f ] x - x g2
246.42
/ f]x - x g
2
=852.75
54
Capítulo 2
por lo tanto:
s=
f ] x - x g2
=
n
852.75
100 =
8.5275 = 2.92 kg
b) Se ordena:
d=x-a
Marca de
Frecuencia (f)
fd
fd 2
clase (x)
61
-6
5
-30
180
64
-3
18
-54
162
67
0
42
0
0
70
3
27
81
243
73
6
8
48
288
n = / f = 100
/ fd =45
/ fd =873
2
por lo tanto:
s=
/ fd
2
n
/ fd
-c n m =
2
873 b 45 l2
100 - 100 =
8.5275 = 2.92 kg
c) Se ordena:
(x)
u
61
-2
64
f
fu
fu 2
5
-10
20
-1
18
-18
18
67
0
42
0
0
70
1
27
27
27
73
2
8
16
32
n = / f = 100
/ fu =15
/ fu
2
=97
por lo tanto:
s=c
/ fu
n
2
/ fu
-c n m = 3
2
97 b 15 l2
100 - 100 = 3 0.9475 = 2.92 kg
2. ESTADÍSTICA DESCRIPTIVA
55
Estadística
Ejemplo 2.4.8
Usa el método de codificación para obtener la desviación estándar para la
distribución de la tabla utilizada en el ejercicio 2.1.13
Solución:
(x)
u
f
fu
fu 2
$2549.5
-2
28
-56
112
$2649.5
-1
20
-20
20
$2749.5
0
36
0
0
$2849.5
1
34
34
34
$2949.5
2
25
50
100
$3049.5
3
30
90
270
$3149.5
4
12
48
192
n = / f = 185
/ fu =146
/ fu
2
=728
por lo tanto:
s=c
/ fu
n
2
/ fu
- c n m = ($100)
2
728 b 146 l2
185 - 185 = ($100) 3.31 = $182
Coeficiente de variación
La variación o dispersión real, determinada a partir de la desviación estándar u otra
medida de dispersión, se denomina dispersión absoluta. Sin embargo, una variación o
dispersión de 10 centímetros al medir una distancia de 100 metros, tiene un efecto muy
diferente si la variación o dispersión de 10 centímetros, se presenta en una distancia
de 10 metros. Una medida de este efecto es sustituida por la dispersión relativa, y se
define como:
Dispersión relativa = Dispersión absoluta / promedio
Si la dispersión absoluta es la desviación estándar s y el promedio es la media x ,
entonces la dispersión relativa se denomina coeficiente de variación; la misma se
denota por V y está dada por:
s
Coeficiente de variación = V = x
que por lo general se expresa en forma de porcentaje.
56
Capítulo 2
Ejemplo 2.4.9
Un fábricante vende focos de 60 (a) y 100 watts (b), los cuales tienen una duración
media de x a = 8760 horas (un año) y x b = 13140 horas (año y medio), respectivamente,
así como desviaciones estándar de sa = 1 750 horas y sb = 2 100 horas. ¿Qué foco posee
la mayor dispersión absoluta y cuál la mayor dispersión relativa?
Solución:
La dispersión absoluta de a es sa = 1750 horas y la de b es sb = 2100 horas, por lo
tanto, el foco de 100 watts (b) tiene mayor dispersión absoluta.
Los coeficientes de variación son:
s
1750
a = xaa = 8760 = 0.20 = 20%
s
2100
b = xbb = 13140 = 0.16 = 16%
Por lo tanto, el foco de 60 watts (a) cuenta con la mayor variación o dispersión relativa.
Ejemplo 2.4.10
El coeficiente de variación del ejemplo 2.4.7 es:
s
2.92
V = x = 67.45 = 0.0433 = 4.3%
EJER
EJERCICIOS 2.4
CIC
2.4.1. Encuentra el rango de los siguientes conjuntos de datos:
a) 1
6
2
6
2
6
3
6
3
7
3
8
4
8
4
9
5
9
5
9
b) 5
6
7
2
4
8
5
9
2
52
7
6
5
6
6
8
4
6
8
3
c) 6.33
7.45
6.15
5.59
6.18
7.01
6.44
5.92
6.12
7.23
d) 35
44
42
50
38
51
32
34
43
55
45
52
61
35
39
36
32
52
34
e) 107.4
102.9
100.9
104.2
117.4
120.0
111.9
106.6
115.3
112.1
116.1
122.0
101.9
121.6
105.3
119.9
108.7
113.4
110.7
118.0
114.5
103.8
109.1
2. ESTADÍSTICA DESCRIPTIVA
57
IOS
Estadística
2.4.2. La mayor de 65 medidas es 52.66 grados centígrados; si el rango es de 32.5 grados,
determina cuál es la medida más pequeña.
2.4.3. Busca la desviación media (DM) de los 5 conjuntos del ejercicio 2.4.1.
2.4.4. Para el conjunto 8, 10, 9, 12, 4, 8, 2 indica la desviación media con respecto a:
a) la media
b) la mediana
Verifica que la desviación media en relación con la mediana no es mayor que la
desviación media con respecto a la media.
2.4.5. A partir de las siguientes tablas de distribución utilizadas en el ejercicio 2.3.12, obtén
la desviación media de cada inciso.
a) Estaturas de 135 estudiantes de una escuela:
Estatura (centímetros)
Número de estudiantes
150 – 154
6
155 – 159
10
160 – 164
17
165 – 169
22
170 – 174
32
175 – 179
24
180 – 184
11
185 – 189
8
190 – 194
4
195 – 199
1
TOTAL 135
b) Estaturas de los mismos 135 estudiantes, pero con mayor intervalo de clases:
58
Capítulo 2
Estatura (centímetros)
Número de estudiantes
150 – 159
16
160 – 169
39
170 – 179
56
180 – 189
19
190 – 199
5
TOTAL 135
c) Peso de 90 hombres que asisten regularmente a una clínica nutricional:
Peso (kilogramos)
Frecuencia
40 – 49.9
4
50 – 59.9
7
60 – 69.9
20
70 – 79.9
26
80 – 89.9
23
90 – 99.9
8
100 – 109.9
2
TOTAL 90
d) Tiempo que tardan 50 automóviles en llegar a 100 km por hora desde 0 km
por hora acelerando al máximo:
Tiempo (segundos)
Frecuencia
2 – 4.99
4
5 – 7.99
15
8 – 10.99
19
11 – 13.99
9
14 o más
3
TOTAL 50
2. ESTADÍSTICA DESCRIPTIVA
59
Estadística
e) Salarios mensuales de 163 trabajadores de una fábrica maquiladora de ropa.
Salarios (pesos)
Número de trabajadores (frecuencia)
3 000 – 3 999
38
4 000 – 4 999
51
5 000 – 5 999
19
6 000 – 6 999
22
7 000 – 7 999
12
8 000 – 8 999
8
9 000 – 9 999
5
10 000 – 14 999
6
15 000 – 50 000
2
TOTAL 163
2.4.6. A partir de los conjuntos del ejercicio 2.4.1, obtén la desviación estándar (s) con la
/ ] x - x g2
primera fórmula / ] x - x g2 y con la fórmula corregida
n
n-1
2.4.7. Con los mismos conjuntos del ejercicio 2.4.1, obtén la varianza (s2) aplicando
ambas fórmulas.
2.4.8. Con las tablas de distribución usadas en el ejercicio 2.4.4, obtén la desviación
estándar y la varianza de cada inciso con la fórmula corregida.
2.4.9. Obtén el coeficiente de variación (V) de los 5 conjuntos del ejercicio 2.4.1 con la
fórmula corregida e indica el porcentaje.
2.4.10. Obtén el coeficiente de variación (V) de cada tabla de distribución de frecuencias
utilizada en el ejercicio 2.4.4 con la primera fórmula para la desviación estándar y
con la fórmula corregida.
2.4.11. Obtén los coeficientes de variación de a) los datos utilizados en el ejercicio
2.3.15, b) los datos del ejercicio 2.3.16, c) los datos del ejercicio 2.3.17 y d) los
datos del ejercicio 2.3.18; con la primera fórmula y con la fórmula corregida
para la desviación estándar.
60
Capítulo 2
2.4.12. A partir de los siguientes datos obtenidos al medir diariamente durante un año la
temperatura de un depósito de agua en grados centígrados, obtén el coeficiente de
variación con la fórmula corregida.
21.36
23.71
15.62
15.04
15.31
23.67
15.68
23.1
15.01
21.69
22.41
17.97
19.17
17.19
16.89
16.46
20.84
22.71
14.99
21.24
17.88
19.73
23.52
22.41
20.37
20.86
20.15
14.01
17.99
21.86
17.67
17.48
21.87
14.91
15.4
17.64
22.29
16.23
20.07
17.87
16.29
23.62
14.41
16.62
22.13
15.54
23.28
14.17
21.04
17.11
17.48
20.61
23.96
20.06
18.6
23.44
22.63
14.85
16.59
19.92
22.89
15.27
16.4
15.74
23.05
22.83
17.24
16.74
20.54
23.87
22.05
20.13
22.95
22.56
22.07
22.58
22.26
21.6
16.15
16.74
23.34
17.4
16.44
15.99
23.82
18.6
19.09
16.65
17.24
21.27
22.45
20.04
20.09
21.35
23.16
23.18
21.3
20.01
19.82
15.22
21.73
17.98
23.94
20.27
21
15.98
22.94
22.98
19.47
23.45
19.9
23.81
17.73
20.84
15.9
20.77
18.84
16.31
23.64
16.18
17.79
15.1
19.04
14.86
23.86
22.27
18.99
17.43
19.04
22.02
21.7
14.83
21.33
20.14
22.25
19.63
14.08
20.58
20.67
23.99
23.54
22.62
18.86
15.49
22.67
21.64
15.14
14.14
14.08
20.99
16.08
17.93
14.62
20.01
19.47
16.29
23.21
15.59
20.59
18.62
19.3
20.73
15.47
15.35
14.21
22.94
17.33
23.68
15.06
23.21
17.62
22.91
14.66
15.98
15.75
22.22
15.27
17.83
14.46
23.32
17.89
14.11
14.98
17.21
18.84
18.17
21.28
19.22
19.05
23.75
22.57
18.79
17.84
19.03
16.52
21.74
18.09
23.43
19.64
19.07
15.39
22.87
16.29
16.47
18.29
19.98
23
19.21
22.92
17.07
15.82
18.12
14.1
19.53
17.67
22.4
19.58
18.7
20.29
18.43
16.59
23.56
15.69
15.74
17.55
21.4
22.85
21.21
23.47
14.94
18.64
15.44
15.92
17.96
15.94
15.1
20.14
18.57
21.19
14.77
14.14
22.29
18.71
22.28
16.51
19.26
23.06
16.88
20.21
22.28
19.34
15.65
23.92
23.89
20.08
19.91
22.05
18.39
20.22
22.08
14.6
18.43
20.6
16.23
16.32
17.17
23.33
18.07
20.07
23.37
15.56
14.03
16.33
23.32
17.54
15.81
19.53
19.76
19.44
23.43
17.4
15.28
18.97
19.62
22.5
22.09
15.37
16.15
15.92
15.46
19.48
16.11
18.57
15.02
19.75
19.55
16.3
20.11
20.66
23.68
16.29
14.12
14.79
21.16
22.31
16.42
15.94
22.73
18.96
19.84
20.55
16.24
17.82
19.84
16.83
20.54
21.37
23.78
23.68
19.9
15.12
20.09
22.22
18.23
20.82
18.58
17.72
18.41
19.38
16.14
21.83
16.34
21.65
18.13
22.59
16.36
15.35
19.83
15.93
14.24
18.93
17.38
17.92
18.05
17.51
19.6
23.5
16.51
19.41
22.1
14.2
22.25
17.94
21.56
16.71
2. ESTADÍSTICA DESCRIPTIVA
61
ESTADÍSTICA
Estadistica cover.indd 1
ESTADÍSTICA
2/18/08 11:14:25 PM