proyecto final de metodos numericos

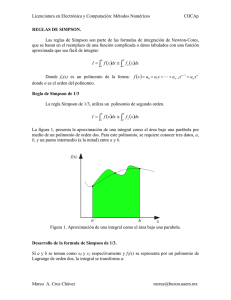
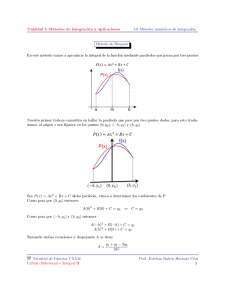
UNIVERSIDAD TECNOLOGICA DE PANAMA
CENTRO REGIONAL UNIVERSITARIO TECNOLOGICO DE
AZUERO
FACULTAD DE INGENIERIA CIVIL
INGENIERIA CIVIL
PROYECTO FINAL DE METODOS NUMERICOS
“METODOS NUMERICOS”
PRESENTADO POR:
BANISTA, JAVIER
BRANDAO, LOURDES
QUINTERO, IVAN
TELLO, JOSSYBETH
FACILITADORA:
MARQUELA DE COHEN
II AÑO
II SEMESTRE
FECHA DE ENTREGA:
13 DE DICIEMBRE DE 2009
ÍNDICE
Introducción…………………………………………………...……………i
I. Contenido
1. Método de Simpson 1/3………………………..……...............4
2. Método de Interpolación de Newton……..……..…………..5
II. Programa…………………………………………………...……….…7
III. Conclusión…………………………………………………………...13
IV. Bibliografía……………………………………………………….....14
INTRODUCCION
Los métodos numéricos son técnicas mediante las cuales es posible formular
problemas matemáticos de tal forma que puedan resolverse usando operaciones
aritméticas.
El análisis numérico trata de diseñar métodos para “aproximar” de una manera
eficiente las soluciones de problemas expresados matemáticamente.
El objetivo principal del análisis numérico es encontrar soluciones “aproximadas” a
problemas complejos utilizando sólo las operaciones más simples de la aritmética.
Se requiere de una secuencia de operaciones algebraicas y lógicas que producen
la aproximación al problema matemático.
Los métodos numéricos pueden ser aplicados para resolver procedimientos
matemáticos en:
Cálculo de derivadas
Integrales
Ecuaciones diferenciales
Operaciones con matrices
Interpolaciones
Ajuste de curvas
Polinomios
Los métodos numéricos se aplican en áreas como: Ingeniería Industrial, Ingeniería
Química, Ingeniería Civil, Ingeniería Mecánica, Ingeniería eléctrica, etc.…
METODOS NUMERICOS
“SIMPSON 1/3”
La regla de Simpson de 1/3 resulta cuando se sustituye un polinomio de segundo
orden en la ecuación:
Si a y b se denominan como x0 y x2 , y f2 (x) se representa mediante un polinomio
de Lagrange de segundo orden, entonces la integral es:
Después de integrar y de reordenar términos, resulta la siguiente ecuación:
“INTERPOLACION DE NEWTON”
El caso más sencillo se presenta cuando queremos interpolar dos puntos,
, obteniéndose la muy conocida función lineal que une dos
puntos:
Si los puntos pertenecen a la gráfica de una función
, la pendiente
,
que tiene una forma de diferencias divididas, representa una aproximación muy
global de la primera derivada de
, con
variando en el intervalo
En el caso de tres puntos
.
, en principio se busca el
polinomio de interpolación de grado dos de la forma
Al evaluar el polinomio en cada uno de los tres puntos y despejando
se obtiene:
,
y
,
Una forma sencilla de hacer los cálculos anteriores es determinando
sucesivamente las entradas de un arreglo triangular:
Donde
para
aparecen los valores
,
En la diagonal de este arreglo triangular
y
.
PROYECTO SEMESTRAL
Código:
Método de Simpson 1/3
Código:
Método de Interpolación de Newton
Código:
CONCLUSION
La ciencia y la tecnología describen los fenómenos reales mediante modelos
matemáticos. El estudio de estos modelos permite un conocimiento más profundo
del fenómeno, así como de su evolución futura. La matemática aplicada es la rama
de las matemáticas que se dedica a buscar y aplicar las herramientas más
adecuadas a los problemas basados en estos modelos. Desafortunadamente, no
siempre es posible aplicar métodos analíticos clásicos por diferentes razones:




No se adecúan al modelo concreto.
Su aplicación resulta excesivamente compleja.
La solución formal es tan complicada que hace imposible cualquier
interpretación posterior.
Simplemente no existen métodos analíticos capaces de proporcionar
soluciones al problema.
En estos casos son útiles las técnicas numéricas, que mediante una labor de
cálculo más o menos intensa, conducen a soluciones aproximadas que son
siempre numéricos. El importante esfuerzo de cálculo que implica la mayoría de
estos métodos hace que su uso esté íntimamente ligado al empleo de
computadores. De hecho, sin el desarrollo que se ha producido en el campo de la
informática resultaría difícilmente imaginable el nivel actual de utilización de las
técnicas numéricas en ámbitos cada día más diversos.
BIBLIOGRAFIA
http://www.uv.es/diaz/mn/fmn.html
http://www.mitecnologico.com/Main/MetodosNumericos
http://es.wikipedia.org/wiki/An%C3%A1lisis_num%C3%A9rico
http://matematicas5.galeon.com/
Apuntes proporcionados por la profesora.