Regla de Simpson - GridMorelos.

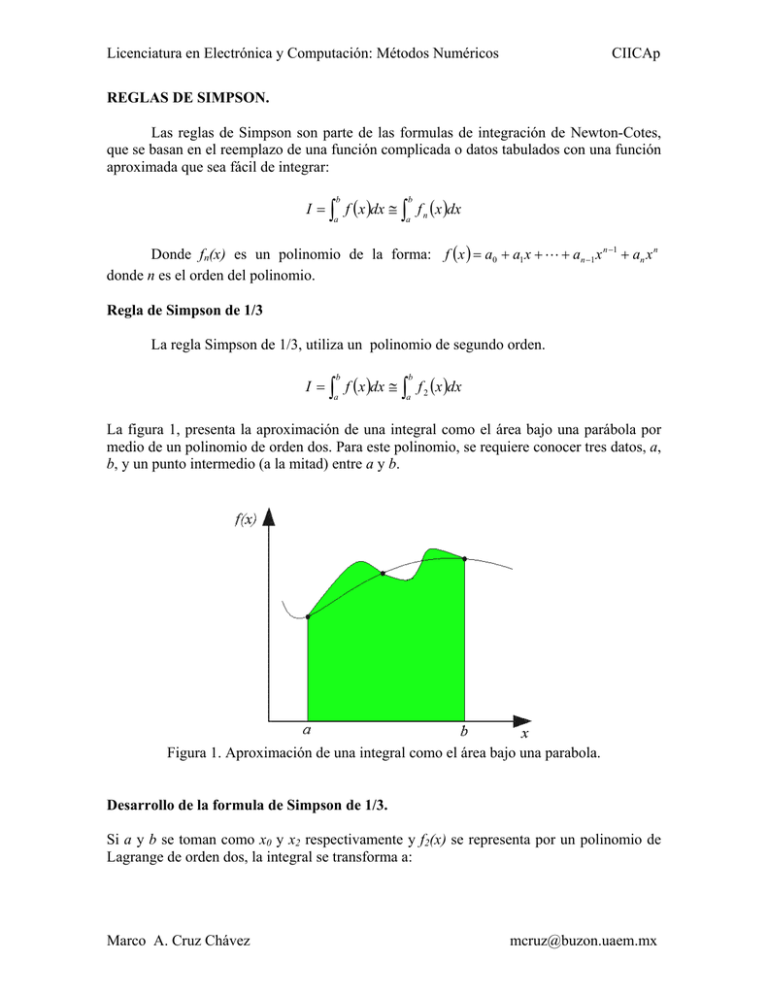
Licenciatura en Electrónica y Computación: Métodos Numéricos
CIICAp
REGLAS DE SIMPSON.
Las reglas de Simpson son parte de las formulas de integración de Newton-Cotes,
que se basan en el reemplazo de una función complicada o datos tabulados con una función
aproximada que sea fácil de integrar:
I = ∫ f ( x )dx ≅ ∫ f n ( x )dx
b
b
a
a
Donde fn(x) es un polinomio de la forma: f ( x ) = a0 + a1 x + L + an −1 x n −1 + an x n
donde n es el orden del polinomio.
Regla de Simpson de 1/3
La regla Simpson de 1/3, utiliza un polinomio de segundo orden.
I = ∫ f ( x )dx ≅ ∫ f 2 (x )dx
b
b
a
a
La figura 1, presenta la aproximación de una integral como el área bajo una parábola por
medio de un polinomio de orden dos. Para este polinomio, se requiere conocer tres datos, a,
b, y un punto intermedio (a la mitad) entre a y b.
Figura 1. Aproximación de una integral como el área bajo una parabola.
Desarrollo de la formula de Simpson de 1/3.
Si a y b se toman como x0 y x2 respectivamente y f2(x) se representa por un polinomio de
Lagrange de orden dos, la integral se transforma a:
Marco A. Cruz Chávez
[email protected]
Licenciatura en Electrónica y Computación: Métodos Numéricos
CIICAp
x2 ⎡ ( x − x )( x − x )
(x − x0 )(x − x2 ) ( ) (x − x0 )(x − x1 ) ( )⎤
1
2
I =∫ ⎢
f ( x0 ) +
f x +
f x dx
x0 ( x − x )( x − x )
(x1 − x0 )(x1 − x2 ) 1 (x2 − x0 )(x2 − x1 ) 2 ⎥⎦
1
0
2
⎣ 0
La integración de la expresión anterior y la ordenación algebraica, da como resultado:
I≅
h
[ f (x0 ) + 4 f (x1 ) + f (x 2 )]
3
h=
I = (b − a )
Donde a = x0, b = x2 y x1 =
(b − a )
2
f ( x0 ) + 4 f ( x1 ) + f ( x 2 )
6
(1)
b+a
2
La ecuación 1 tiene el formato de un área trapezoidal donde:
I = ancho x altura promedio
(2)
Aplicación múltiple de la regla de Simpson 1/3.
Para mejorar la exactitud de la regla de Simpson de 1/3, se puede dividir el intervalo de
integración [a, b], en n segmentos iguales y aplicar a cada uno de ellos la ecuación 1.
Finalmente sumar los resultados para obtener el área total de integración. Cada segmento
tiene un valor de:
h=
b−a
n
Hay n + 1 puntos igualmente espaciados entre el intervalo de a y b, esto es x0, x1, x2,…,xn.
Si se designa a los extremos de estos puntos como x0 = a y xn = b. la integral se puede
representar como
x2
x4
xn
(3)
I = f ( x )dx + f ( x )dx + L +
f (x )dx
∫
x0
Marco A. Cruz Chávez
∫
x2
∫
xn − 2
[email protected]
Licenciatura en Electrónica y Computación: Métodos Numéricos
CIICAp
Se sustituye la regla de Simpson 1/3 (Ec. 1) en cada integral de la ecuación (3)
I ≅ 2h
f ( x0 ) + 4 f ( x1 ) + f ( x 2 )
f ( x 2 ) + 4 f ( x3 ) + f ( x 4 )
f (x n − 2 ) + 4 f ( x n −1 ) + f ( x n )
+ 2h
+ L + 2h
6
6
6
Agrupando términos y sustituyendo el valor de h se tiene:
f (x0 ) + 4
n −1
∑
f ( xi ) + 2
n−2
∑ f (x ) + f (x )
j
n
I = (b − a )
123
3n
Ancho 14444444244444443
i =1, 3, 5
Altura
j =2, 4,6
promedio
Ejercicio:
a) Usar 4 segmentos de la regla de Simpson 1/3 para estimar la integral de
f ( x ) = 0.2 + 25 x − 200 x 2 + 675 x 3 − 900 x 4 + 400 x 5
Utilice el intervalo desde a = 0 hasta b = 0.8
b) Compruebe con el valor correcto de la integral.
Marco A. Cruz Chávez
[email protected]