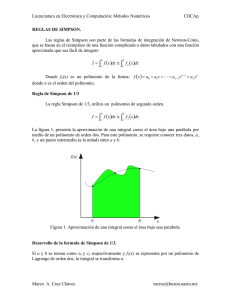
Document

Métodos Numéricos
TEMA 8:
DERIVACION E INTEGRACION
Numérica
DIFERENCIACIÓN NUMÉRICA
Polinomio de interpolación es aplicable para la resolución de
problemas de diferenciación, en general y el cálculo de derivadas, en
particular.
Dada una tabla de valores de la función f(x) para diversos valores de
x, se puede determinar el polinomio de interpolación que, satisfaciendo
a los valores dados, represente con cierto grado de aproximación a f(x).
De acuerdo a lo anterior, es posible calcular, de manera más o
menos precisa, la derivada f'(x), de la función en cuestión.
Se puede hallar en general y por única vez, las derivadas sucesivas
de la fórmula de interpolación y aplicarlas a cada caso particular.
1
Derivación numérica (1/2)
ETSII-UPM
Se trata de evaluar numéricamente la derivada de una función f(x) a
partir de valores numéricos de dicha función.
Se puede comenzar con una aproximación intuitiva y geométrica
– De la definición de derivada como límite, se puede aproximar la derivada:
–
–
– Geométricamente se pueden considerar tres variantes:
–fórmula avanzada
fórmula atrasada
fórmula centrada
f(x+h)
f(x)
f(x)
f(x+h)
f(x−h)
f(x−h)
f(x)
x
x+h
x−h
x
x−h
x
x+h
Derivación numérica (2/2)
ETSII-UPM
En el cálculo numérico de derivadas se cometen errores importantes
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
En principio, parece evidente que al disminuir h se reduce el error.
Ejemplo: derivada de ex en x=1 (valor exacto 2.71828182845905)
h
1e-01
1e-02
1e-03
1e-04
1e-05
1e-06
1e-07
1e-08
1e-09
1e-10
1e-11
1e-12
1e-13
1e-14
f(x+h)
3.00416602394643
2.74560101501692
2.72100146988158
2.71855367023375
2.71830901141324
2.71828454674223
2.71828210028724
2.71828185564186
2.71828183117733
2.71828182873087
2.71828182848623
2.71828182846176
2.71828182845932
2.71828182845907
f(x+h)-f(x)
0.28588419548739
0.02731918655787
0.00271964142253
0.00027184177471
0.00002718295420
0.00000271828319
0.00000027182820
0.00000002718282
0.00000000271828
0.00000000027183
0.00000000002718
0.00000000000272
0.00000000000027
0.00000000000003
f'(x)
2.85884195487388
2.73191865578708
2.71964142253278
2.71841774707848
2.71829541991231
2.71828318698653
2.71828196396484
2.71828177744737
2.71828159981169
2.71827893527643
2.71827005349223
2.71827005349223
2.71338507218388
2.66453525910038
error
-0.14056012641483
-0.01363682732803
-0.00135959407374
-0.00013591861944
-0.00001359145326
-0.00000135852748
-0.00000013550580
0.00000005101167
0.00000022864736
0.00000289318262
0.00001177496681
0.00001177496681
0.00489675627516
0.05374656935867
El error disminuye con h al principio, pero hay un momento en que aumenta.
El error mínimo se produce aproximadamente cuando h=log10(eps)/2.
2
Análisis del error
ETSII-UPM
Fórmulas avanzadas
– Se pueden obtener a partir del desarrollo en serie de Taylor:
f ( x + h) = f ( x) + f ′( x)h +
f ′′(ζ ) 2
h
2!
⇒
f ′( x) =
f ( x + h) − f ( x) f ′′(ζ )
−
h
h
2!
y en este caso se dice que el error es de orden 1 ó orden h: O(h).
Para la fórmula centrada
– Se realiza el desarrollo en serie de Taylor en x+h y en x−h:
f ′′( x) 2 f ′′′(ζ 1 ) 3
–
f ( x + h) = f ( x) + f ′( x)h +
h +
h
2!
3!
–
f ′′( x) 2 f ′′′(ζ 2 ) 3
f ( x − h) = f ( x) − f ′( x)h +
h −
h
–
2!
3!
– Restando miembro a miembro y suponiendo que f''' es continua:
f ( x + h) − f ( x − h) = 2hf ′( x) + ( f ′′′(ζ 1 ) + f ′′′(ζ 2 ) )
h3
h3
= 2hf ′( x) + 2 f ′′′(ζ )
3!
3!
de donde se llega finalmente a:
–
f ( x + h) − f ( x − h)
h 2 f ( x + h) − f ( x − h)
+ f ′′′(ζ ) =
+ O (h 2 )
f ′( x) =
2h
3!
2h
–
– La fórmula centrada es de orden 2 y por tanto más precisa que las otras dos.
DERIVACION MEDIANTE FORMULAS DE
INTERPOLACION
La metodología descripta implica el uso de cualquiera de las
fórmulas de interpolación estudiadas. Se desarrolla un caso
particular.
La fórmula de NEWTON-GREGORY Ascendente, en la cual se ha
hecho la transformación x=x0 +hu, para facilitar su uso:
f ( x ) = f ( x0 + hu ) = f ( x0 ) + ∆f ( x0 )u + ∆2 f ( x0 )
+ ∆3 f (x0 )
u(u − 1)(u − 2)
+K
3!
u(u − 1)
+
2!
(8.1)
3
DERIVACION MEDIANTE FORMULAS DE
INTERPOLACION (2)
Derivando respecto de la variable u, se obtiene:
h f ′(x0 + hu ) = ∆f (x0 ) + ∆2 f (x0 )
2u − 1 3
3u 2 − 6u + 2
+ ∆ f ( x0 )
+K
2
6
y para x=x0 ; vale decir, para u=0, resulta la ecuación:
1
1
1
h f ′( x0 ) = ∆f (x0 ) − ∆2 f ( x0 ) + ∆3 f (x0 ) − ∆4 f (x0 ) +K
2
3
4
(8.2)
DERIVACION MEDIANTE FORMULAS DE
INTERPOLACION (3)
Análogamente, para la derivada segunda se obtiene la expresión:
h 2 f ′′( x0 + hu ) = ∆2 f ( x0 ) + ∆3 f ( x0 )(u − 1) + ∆4 f ( x0 )
6u 2 − 18u + 11
+K
12
y para x=x0 ; o sea, haciendo u=0, resulta la ecuación:
h 2 f ′′( x0 ) = ∆2 f (x0 ) − ∆3 f ( x0 ) +
11 4
∆ f ( x0 ) −K
12
(8.3)
Este procedimiento puede ser iterado tantas veces como se necesite,
para obtener derivadas de mayor orden.
4
DERIVACION MEDIANTE FORMULAS DE
INTERPOLACION (4)
Si se parte de la fórmula de NEWTON-GREGORY Descendente o, de
las de GAUSS, LAGRANGE, BESSEL, etc., se encontraran, nuevas
fórmulas de derivación para cada caso en particular, las que, ofrecerán
mayor o menor precisión según la posición relativa del valor de la
variable para el cual se desea calcular las derivadas
DERIVACION MEDIANTE FORMULAS DE
INTERPOLACION (5)
La aplicación de idéntico criterio para la fórmula de NEWTONGREGORY Descendente:
f (xn + hu ) = f ( xn ) + u∇f (xn ) +
u(u + 1) 2
u(u + 1)(u + 2 ) 3
∇ f ( xn ) +
∇ f ( xn ) +K
2!
3!
da como resultado derivando con respecto a u e igualando a cero:
1
1
h f ′( xn ) = ∇f (xn ) + ∇ 2 f ( xn ) + ∇ 3 f ( xn ) +K
2
3
(8.4)
como así también:
h 2 f ′′( xn ) = ∇ 2 f ( xn ) + ∇ 3 f ( xn ) +
11 4
∇ f ( xn ) +K
12
(8.5)
5
ALGORITMO DE HORNER
Otro método idóneo para determinar el valor de las derivadas
sucesivas, en el especial caso de que la función en cuestión sea una
expresión algebraica, es el denominado MÉTODO o ALGORITMO
DE HORNER
Este método, tiene la ventaja adicional que permite calcular el valor
de la función para el valor de la variable en el cual se pretende
determinar sus derivadas y, además, de ser de muy sencilla aplicación:
INTRODUCCION
En ocasiones es necesario determinar el valor numérico de una función
algebraica polinómica, de la forma:
P( x ) = a0 x n + a1 x n −1 + a2 x n − 2 +K+ an −1 x + an
(8.6)
Será estudiado a continuación el caso de tener que calcular el valor de
la función en un punto α.
Todos los desarrollos que siguen tienen validez tanto para valores de α
reales, como complejos, pero se entenderá que el número de
operaciones a efectuarse solo es válido en el campo real.
6
INTRODUCCION (2)
Si se calculara directamente su valor reemplazando el de x por el de α,
resulta:
(8.7)
n
n −1
P(α ) = a0α + a1α +K+ an −1α + an
Se deben calcular α2 ; α3 ;...; αn ; es decir, n-1 multiplicaciones.
Después deben ser formados los productos a0 αn ; a1 αn-1 ;...; an-1 α ; o
sea, n multiplicaciones más.
En total se deben realizar 2n-1 multiplicaciones y n adiciones para
calcular el valor de P(α) a partir de la expresión (8.6), haciendo uso
directo de la fórmula (8.7).
INTRODUCCION (3)
Una alternativa dada por HORNER, permite disminuir prácticamente
a la mitad el número de operaciones, con la posibilidad adicional de
calcular también sus derivadas sucesivas en el mismo punto α:
P'(α); P"(α);...; P(n)(α).
7
CALCULO DEL VALOR DEL POLINOMIO
Una manera recurrente de escribir la expresión (8.7) es la siguiente
P(α ) = (K (((a0α + a1 )α + a2 )α + a3 )α +K+ an −1 )α + an
que puede obtenerse directamente haciendo uso del algoritmo (8.8)
b0 = a0
b1 = b0 α + a1
b2 = b1 α + a2
. . . . . . . . .
bn-1 = bn-2 α + an-1
P(α) =bn = bn-1 α + an
El valor de bn es el de P(x) cuando x=α; vale decir, el de P(α).
En total son necesarias n multiplicaciones y n adiciones, para lograr el
resultado anterior
Ejemplo (i):
p(x) = 4 x 4 + 3 x 3 - 2x 2 + 4 x - 8 , x 0 = 2
Extrayendo factor común x en los primeros 4
términos, luego en los 3 primeros,
y finalmente en los 2 primeros términos, se
tiene:
p(x) = (4 x 3 + 3 x 2 - 2x + 4)x - 8 ;
p(x) = ((4 x 2 + 3 x - 2)x + 4)x - 8 ;
p(x) = ( ((4 x + 3) x - 2)x + 4)x - 8
8
Algoritmo de Horner
Algoritmo:
E1) Ingresar n (grado polinomio); ai (coeficientes); x0
valor para el cual se evalúa p(x)
E2) Asignar: bn ← an
E3) Para k = n-1, n-2, ... , 0 hacer :
b k ← b k +1x 0 + a k
E4) Imprimir: “Valor de P(x0) = “; b0 ;
Ejemplo (ii):
Evaluamos ahora los paréntesis de esta última
expresión de p(x), desde el más interior, (4x+3),
para
x0=2 y así siguiendo, hasta el último:
1) 4x + 4 en x = 2 es igual a 11
2) (11)x - 2 en x = 2 es 20
3) (20)x + 4 en x = 2 es 44
4) (44)x - 8 en x = 2 es 80
9
Ejemplo (iii):
Por lo tanto: p(2) = 80
El algoritmo de Horner para este ejemplo donde
grado p(x) es 4 y los coeficientes ai permite
escribir:
p(x) = ((( a 4 x + a 3 )x + a 2 )x + a 1 )x + a 0
Ejemplo (iV):
Nota:
Ventaja importante el ahorro de operaciones,
disminuyendo así los efectos de la
propagación de errores.
Obsérvese en el ejemplo que el método
usual necesita 10 multiplicaciones y 4 sumas
(restas); en cambio, con la regla de Horner,
se efectúan 4 multiplicaciones y 4 sumas.
10
CALCULO DE LAS DERIVADAS SUCESIVAS
Para calcular las derivadas sucesivas de P(x) en el punto x=α, es
necesario utilizar un simple artificio. La expresión:
P( x ) = a0 x n + a1 x n −1 + a2 x n − 2 +K+ an −1 x + an
P(x) = (x-α) [b0 xn-1 + b1 xn-2 + ... + bn-2
(8.6) se puede
escribir
x + bn-1 ] + bn (8.9)
dado que se puede reconstruir la (8.6) a partir de la (8.9); realizando las
operaciones indicadas, resulta:
P(x) = b0 xn - α b0 xn-1 + b1 xn-1 - α b1 xn-2 + ... +
+ bn-2 x2 - α bn-2 x + bn-1 x - α bn-1 + bn
= b0 xn + (b1 - α b0 ) xn-1 + (b2 - α b1 ) xn-2 + ... +
+ (bn-1 - α bn-2 ) x + (bn - α bn-1 )
CALCULO DE LAS DERIVADAS SUCESIVAS
(2)
Comparando esta última expresión con la (8.6) e igualando sus
coeficientes homólogos se pueden despejar los b j de la siguiente
manera:
a0 = b0
a1 = b1 - α b0
. . . . . . . . .
an-1 = bn-1 - α bn-2
an = bn - α bn-1
⇒ b0 = a0
⇒ b1 = a1 + α b0
. . . . . . . . . .
⇒ bn-1 = an-1 + α bn-2
⇒ bn = an + α bn-1
como se quería demostrar.
11
CALCULO DE LAS DERIVADAS SUCESIVAS
(3)
Llamando Q1 (x) al polinomio encerrado dentro del corchete de la
siguiente expresión:
P(x) = (x-α) [b0 xn-1 + b1 xn-2 + ... + bn-2 x + bn-1 ] + bn (8.9)
Puede escribirse P (x) = (x - a) Q1 (x) + bn
(8.10)
donde el resto bn es constante e igual a P(α), como ya se ha visto.
Derivando respecto de x la expresión (8.10), resulta:
P’(x) = Q1 (x) + (x - a) Q1’(x)
(8.11)
de la que es posible inferir que:
P’(α) = Q1 (α)
(8.12)
CALCULO DE LAS DERIVADAS SUCESIVAS
(4)
Expresión, que puede ser escrita en forma recurrente y similar a la
(8.8), de la manera siguiente:
P′(α ) = (K (((b0α + b1 )α + b2 )α + b3 )α +K+ bn −1 )α + bn −1
cuyo algoritmo resolutorio, es:
c0 = b0
c1 = b1 + α c0
c2 = b2 + a c1
. . . . . . . . .
P’(α) = cn-1 = bn-1 + α cn-2 = Q
Se definen los coeficientes c i de modo que al final del proceso se
obtenga el valor buscado en: Q1 (α ) = P’(α)
12
CALCULO DE LAS DERIVADAS SUCESIVAS
(5)
Para determinar las siguientes derivadas sucesivas del polinomio P(x)
en el punto x=α, es necesario hacer las siguientes consideraciones.
1. Escribiendo el polinomio P(x) en términos de la fórmula del
desarrollo en serie de Taylor, resulta:
P ( x ) = P (α ) + ( x − α )P′(α ) +
(x − α )2 P′′(α ) +K+ (x − α )n P ( n) (α )
2!
n!
CALCULO DE LAS DERIVADAS SUCESIVAS
(6)
2. De
P (x) = (x - a) Q1 (x) + bn y considerando que
bn=P(α), se puede escribir que:
Q1 ( x ) =
P( x ) − P (α )
x −α
3. Teniendo en consideración estas dos últimas expresiones, resulta:
Q1 ( x ) = P′(α ) +
(x − α ) P′′′(α ) +K+ (x − α )
x −α
P′′(α ) +
2!
3!
n!
2
n −1
P ( n ) (α )
4. Sacando factor común x-α, se obtiene:
n−2
 P′′(α ) x − α

(
x −α )
′
′
′
′
Q1 (x ) = P (α ) + ( x − α )
+
P (α ) +K+
P ( n ) (α )
3!
n!
 2!

13
CALCULO DE LAS DERIVADAS SUCESIVAS
(7)
5. Llamando, finalmente, Q2 (x) al polinomio encerrado dentro del
corchete, resulta:
Q1 (x) = P’(α) + (x - α) Q2 (x)
Derivando esta última expresión se obtiene
Q1’ (x) = Q2 (x) + (x - α) Q2’ (x)
que, en el punto x=α, vale:
Q1’ (x) = Q2 (x)
(8.13)
CALCULO DE LAS DERIVADAS SUCESIVAS
(8)
Derivando la siguiente expresión respecto de x, se obtiene:
P’(x) = Q1 (x) +(x - a) Q1’(x)
(8.11)
P”(x) = 2 Q1’ (x) + (x - a) Q1”(x)
la cual, a su vez, en el punto x=α, toma el valor:
P”(α) = 2 Q1’ (α)
(8.14)
Q1’ (x) = Q2 (x)
(8.13 )
Considerando las expresiones (8.13) y (8.14), se obtiene en definitiva
P”(α) = 2 Q2 (α)
(8.15)
14
CALCULO DE LAS DERIVADAS SUCESIVAS
(9)
Con mayor grado de generalización, es posible calcular las siguientes
derivadas sucesivas de P(x), en el punto x=α.
Iterando el procedimiento descripto anteriormente, se puede escribir,
en general:
P ( k −1) (α )
(8.16)
Qk −1 ( x ) =
+ ( x − α )Qk ( x )
(k − 1)!
de donde:
Qk ( x ) =
(x − α )
Pk (α ) ( x − α )
+
P ( k +1) (α ) + K +
(k + 1)!
k!
n!
k +1
n−k
P ( n ) (α )
(8.17)
CALCULO DE LAS DERIVADAS SUCESIVAS
(10)
Derivando la (8.16) con respecto a x, se deduce que:
Qk-1’ (x) = Qk (x) + (x - α) Qk’ (x)
en la cual, haciendo x=α, resulta:
Qk-1’ (α) = Qk (α)
Considerando la expresión (8.17), se obtiene:
(k )
Qk = P (α )
k!
15
CALCULO DE LAS DERIVADAS SUCESIVAS
(11)
Con mayor grado de generalización, es posible calcular las
siguientes derivadas sucesivas de P(x), en el punto x=α.
En definitiva, es posible deducir que, en general, la derivada de orden
k-ésimo resulta:
P(k)(α) = k! Qk (α)
(8.18)
que representa la expresión general de la derivada de orden k, de un
polinomio P(x), en el punto x=α.
Introducción a la integración numérica
ETSII-UPM
Planteamiento del problema
– Se trata de evaluar la integral definida de una función mediante un sumatorio
de valores de esa función en ciertos puntos llamados nodos, multiplicados por
unos coeficientes de ponderación llamados pesos:
∫
b
a
n
f ( x)dx = ∑ wi f ( xi ) = w1 f1 + w2 f 2 + ... + wn f n
i =1
– Esta expresión implica la sustitución de un sumatorio infinito (la integral) por
un sumatorio finito, por lo que se producirá un error de truncamiento.
– Se llama grado de precisión de la fórmula de integración al máximo grado de
los polinomios que son integrados exactamente por dicha fórmula.
– Para deducir las fórmulas de integración numérica la función f(x) se suele
sustituir por el polinomio de interpolación p(n)(x) y realizar la integración
exacta de este polinomio.
– Si un polinomio de grado n es integrado exactamente es de esperar que el error
en la integración numérica de la función f(x) dependa de la derivada de orden
(n+1) de dicha función en un punto perteneciente al intervalo de integración.
– La integración numérica es un proceso más estable y preciso que la derivación
numérica vista previamente.
16
Fórmulas de Newton-Cotes (1/4)
ETSII-UPM
Se basan en el polinomio de interpolación de Newton con
argumentos igualmente espaciados (fórmula de diferencias finitas).
Algunas fórmulas de Newton-Cotes:
Regla trapezoidal
∫
x1
Regla de Simpson
∫
x2
∫
x3
∫
x4
x0
x0
3
8
Regla de Simpson
–
Regla de Boole
–
x0
x0
h
( f0 + f1 )
2
h
f ( x)dx ≈ ( f 0 + 4 f1 + f 2 )
3
3h
f ( x)dx ≈ ( f 0 + 3 f1 + 3 f 2 + f3 )
8
2h
f ( x)dx ≈
( 7 f0 + 32 f1 + 12 f 2 + 32 f3 + 7 f 4 )
45
f ( x)dx ≈
h3
f ′′(ζ )
12
5
h (iv )
err = −
f (ζ )
90
5
3h ( iv )
err = −
f (ζ )
80
8h7 ( vi )
err = −
f (ζ )
945
err = −
Observaciones:
–
–
–
–
En estas fórmulas se supone xk=x0+kh.
Los errores dependen de potencias elevadas de h.
La fórmula de Simpson tiene una alta relación precisión/coste.
No se suelen utilizar fórmulas de orden muy grande porque aparecen
coeficientes negativos que dan lugar a problemas numéricos.
Fórmulas de Newton-Cotes (2/4)
ETSII-UPM
Deducción de la regla de Simpson 3/8
– Se parte del polinomio de interpolación de Newton en diferencias finitas:
1
∆ 2 y0
∆ 3 y0
–
p ( n ) ( x) = y0 + ∆y0 ( x − x0 ) +
( x − x0 )( x − x1 ) +
( x − x0 )( x − x1 )( x − x2 )
2
h
2!h
3!h3
–
( x − x0 ) = sh
– Haciendo el cambio de variable x = x0 + sh
–
x = x1 + ( s − 1)h
( x − x1 ) = ( s − 1) h
–
x = x2 + ( s − 2) h ( x − x2 ) = ( s − 2) h
– Se llega a:
L
–
s( s − 1) 2
s( s − 1)( s − 2) 3
∆ y0 +
∆ y0 =
2!
3!
s( s − 1)
s ( s − 1)( s − 2)
= y0 + s( y1 − y0 ) +
( ( y2 − y1 ) − ( y1 − y0 ) ) +
( ( ( y3 − y2 ) − ( y2 − y1 ) ) − ( ( y2 − y1 ) − ( y1 − y0 ) ) ) =
2!
3!
s( s − 1)
s( s − 1)( s − 2)
= y0 + s( y1 − y0 ) +
( y2 − 2 y1 + y0 ) ) +
( y3 − 3 y2 + 3 y1 − y0 )
2!
3!
p ( n ) ( s ) = y0 + s∆y0 +
9
3
– Teniendo en cuenta que ∫0 sds = 2 ;
1 3
9
s( s − 1)ds = ;
2! ∫0
4
1 3
3
s ( s − 1)( s − 2)ds =
3! ∫0
8
se obtiene finalmente, después de reordenar términos:
∫
x3
x0
3
p (3) ( x )dx = h ∫ p (3) ( s)ds =
0
3h
( y0 + 3 y1 + 3 y2 + y3 )
8
17
Fórmulas de Newton-Cotes (4/4)
ETSII-UPM
El cálculo de los errores de las restantes fórmulas de Newton-Cotes
es bastante laborioso y no se incluye en estas trasparencias.
Interpretación gráfica de la regla trapezoidal y las dos reglas de
Simpson:
E=−
1
f ′′(ξ )h3
12
E=−
1 iv
f (ξ )h5
90
E=−
3 iv
f (ξ )h5
80
Fórmulas abiertas y cerradas
ETSII-UPM
Concepto de fórmula de integración abierta
– Se llama abierta a una fórmula de integración numérica que no evalúa la
función integrando en uno o en los dos extremos del intervalo.
– Las fórmulas abiertas son útiles cuando no se conoce la función en un extremo
o tiene un valor infinito (integrales impropias).
– Un caso de gran interés práctico son las fórmulas de Adams, que utilizan n
puntos, pero sólo desean calcular la integral en el último tramo (ver figuras)
abierta
cerrada
abierta
cerrada
Newton-Cotes
Adams
18
INTEGRACIÓN NUMÉRICA
Dentro del campo analítico, perteneciente a la matemática pura, se
desconoce la primitiva de la mayor parte de las funciones que ella
estudia o si esta se conoce, su aplicación es larga y compleja, para
utilizarla con provecho en la resolución de una integral.
Incluso, es posible que se desconozca la expresión analítica de la
función sobre la cual se desea integrar.
Consecuentemente, y en términos generales, es posible asegurar
que la gran mayoría de los problemas que se presentan en la práctica,
carecen de solución dentro del campo analítico.
INTEGRACIÓN NUMÉRICA (2)
Resumiendo, la imposibilidad, o la inconveniencia, de la aplicación de
métodos tradicionales está dada, fundamentalmente, por :
I.- Que no se conozca ninguna primitiva de aquella función que
es necesario integrar,
II.- Que aún conociéndose una función primitiva, su aplicación
resulte excesivamente compleja o extensa,
III.- Que, directamente, se desconozca la expresión analítica de
la función que debe ser integrada.
19
INTRODUCCION
Cuando el problema en cuestión consiste en calcular la integral definida
de una determinada función f(x), dada por:
I = ∫ f ( x )dx
b
(8.19)
a
y se conoce una función F(x), primitiva de f(x), es decir, F' (x) = f(x),
se aplica la regla de BARROW :
I=
x =b
∫ f (x )dx = F (b ) − F (a )
(8.20)
x=a
INTRODUCCION (2)
Cuando no se conoce ninguna primitiva de la función , resulta
necesario apelar a métodos de cálculo aproximados. Igual proceder
debe adoptarse si, aún conociéndose una primitiva, resulta poco
práctico aplicarla, por su complejidad.
En ocasiones se cuenta solamente con una tabla de alguno de sus
valores, proveniente de resultados experimentales; en cuyo caso,
tampoco es posible aplicar la regla de BARROW.
Considerando que la integral dada por (8.19) equivale a determinar
el valor del área bajo la curva de la función f(x), es posible desarrollar
diversos métodos aproximados para lograr dicho objetivo.
20
FORMULA DE LOS TRAPECIOS
Supónganse conocidos los n+1 valores x0 ; x1 ;...; xn deducidos de la
función f(x), conocida, que cumplen con la condición:
xk - xk-1 = h
para
k = 1; 2; ... ; n
Una primera aproximación al valor del área a calcular, limitada por
los puntos x0 ; A0 ; A1 ; ... ; An ; xn se obtiene considerando la suma
de las áreas de los trapecios inscriptos en cada una de las superficies
parciales limitadas por los puntos,
x0 ; A0 ; A1 ; x1
x1 ; A1 ; A2 ; x2
. . . . . . . . .
xn-1 ; An-1 ; An ; xn
FORMULA DE LOS TRAPECIOS (2)
Figura 8.1.
An
A n -1
A1
A2
f (x )
A0
Y0
Y2
Y1
h
0
X0
h
X1
Yn
Yn -1
h
X2
X n -1
Xn
21
FORMULA DE LOS TRAPECIOS (3)
En consecuencia, resulta:
área (x0 ; A0 ; A1 ; x1 ) ≈ 1 / 2 ( y0 + y1 ) h
área (x1 ; A1 ; A2 ; x2 ) ≈ 1 / 2 ( y1 + y2 ) h
. . . . . . . . . . . . . . . . . . . . .
área (xn-1 ; An-1 ; An ; xn) ≈ 1 / 2 ( yn-1 + yn ) h
Sumando las expresiones de las áreas así obtenidas, resulta
h
∫ f (x )dx ≅ 2 ( y
xn
x0
0
+ 2 y1 +K+ 2 y n −1 + y n )
(8.21)
FORMULA DE LOS TRAPECIOS (4)
La fórmula de los trapecios tiene una precisión suficientemente buena
cuando se trata de aplicarla a determinaciones que no requieran una
aproximación de orden elevado.
En el caso de haberse sustituido la curva, dada por la función continua
f(x), mediante la poligonal inscripta, descripta mediante los puntos
dados o calculados, el modelo realizado puede clasificarse como una
Discretización; y no satisface plenamente cuando se trata de obtener
gran precisión.
22
FORMULA DE SIMPSON (1)
Basado en la utilización de segmentos de parábola para aproximar
los arcos de curva, en lugar de emplear segmentos de recta;es decir
utilizar curvas en lugar de una poligonal, se obtiene una mayor
precisión en el cálculo de integrales definidas.
Primeramente se considerará el caso de la parábola de segundo
grado, a partir del que se deducirá la expresión analítica de la
fórmula de SIMPSON.
FORMULA DE SIMPSON (2)
Y
A0
Figura 8.2
A1
A2
Y0
Y1
−h
X0
h
0
Y2
X2
X1
23
FORMULA DE SIMPSON (3)
El primer paso consiste en determinar el área comprendida entre el eje
de las x, la parábola de eje vertical que pasa por los tres primeros
puntos dados y sus ordenadas extremas.
Llamando A0 ; A1 ; A2 a los puntos mencionados y suponiendo que
tienen abscisas equidistantes; es decir, que:
x1 - x0 = x2 - x1 = h
Considerando, además que, haciendo pasar el eje y por el punto
intermedio A1 no se pierde generalidad (ver figura 8.2).
FORMULA DE SIMPSON (4)
Dadas estas condiciones y teniendo en cuenta que, en general, la
parábola de segundo grado es:
y = a x2 + b x + c
pero, como debe pasar por los tres puntos A0 ; A1 ; A2 , es posible
escribir:
y0 = a x02 + b x0 + c = a (-h)2 + b (-h) + c = a h2 - b h +c
y1 = a x12 + b x1 + c = c
y2 = a x22 + b x2 + c = a h2 + b h + c = a h2 + b h +c
24
FORMULA DE SIMPSON (5)
Sumando y restando la primera y la última de estas expresiones, y
directamente de la segunda, se obtienen los siguientes valores:
a=
y2 − 2 y1 + y0
y − y0
;b = 2
;c = y1
2
2h
2h
Valores que serán empleados para reemplazarlos en la expresión de la
integral
FORMULA DE SIMPSON (6)
Por otra parte, del análisis sabemos que la expresión analítica del área
buscada vale:
h
h
h
 x3

x2
2
2
I = ∫ ydx = ∫ (a x + b x + c )dx = a + b + c x  = ah 3 + 2ch
−h
−h
2
 3
 −h 3
Reemplazando en esta última los valores de a y c anteriormente
obtenidos, resulta:
I=
2 y2 − 2 y1 + y0 3
h
h
h + 2 y1 h = ( y2 − 2 y1 + y0 + 6 y1 ) = ( y0 + 4 y1 + y2 )
2
3
2h
3
3
El conocimiento de tres ordenadas es suficiente para determinar el área
limitada por el arco de parábola cuadrática que pasa por los puntos
correspondientes.
25
FORMULA DE SIMPSON (7)
En el caso de que la curva se encuentre descripta mediante una tabla
compuesta de n+1 puntos A0 ; A1 ; ...; An , siendo n un número par y
con abscisas x0 ; x1 ; ...; xn equidistantes, es posible aplicar la
metodología expuesta, cada tres puntos (A0 ; A1 ; A2 ); (A2 ; A3 ; A4 );
etc. y, de este modo, obtener la expresión:
xn
I = ∫ f ( x)dx ≅
x0
h
( y0 + 4 y1 + y2 ) + h ( y2 + 4 y3 + y4 ) + K + h ( yn−2 + 4 yn −1 + yn )
3
3
3
FORMULA DE SIMPSON (8)
De donde, considerando a los operadores E, P, I con idéntico
significado al establecido en el punto anterior, se obtiene:
I = ∫ f (x )dx ≅
xn
x0
h
(E + 4I + 2P )
3
(8.23)
Esta última expresión es la conocida e importante FORMULA DE
SIMPSON, muy utilizada para determinaciones expeditivas.
26
REGLA DE LOS TRES OCTAVOS DE
SIMPSON
Como es fácil apreciar, la fórmula de SIMPSON , solo es válida y
utilizable en el caso en que se haya subdividido el intervalo de
integración en un número de franjas tal, que la cantidad de puntos
resultantes; vale decir, los que describen la curva y = f(x), sea impar.
Esto sucede cuando el número de franjas aludido es par.
El mismo Simpson ha desarrollado una fórmula utilizable en el caso
que el número n de franjas sea impar.
REGLA DE LOS TRES OCTAVOS DE
SIMPSON (2)
Figura 8.3
Y
A1
A2
A3
A0
Y0
−3
H
2
Y1
−
H
2
0
Y3
Y2
H
2
3
H
2
27
REGLA DE LOS TRES OCTAVOS DE
SIMPSON (3)
La deducción de la correspondiente fórmula es similar a la realizada
para la de SIMPSON, excepto que, para la determinación de las áreas
parciales, es necesario utilizar parábolas de tercer grado que conecten
cuatro puntos consecutivos de la curva en cuestión.
La forma general de la ecuación de tercer grado representada por una
parábola cúbica es:
y = a x3 + b x2 + c x + d
(8.24)
REGLA DE LOS TRES OCTAVOS DE
SIMPSON (4)
Para determinar los valores de los parámetros a; b; c; d es necesario
imponer a la expresión (8.24), la condición que pase por los cuatro
puntos A0 ; A1 ; A2 ; A3 y ubicar el eje de las y como se indica en la
figura 8.3, lo cual no hace perder generalidad al razonamiento; con
ello el intervalo de integración resulta:
−
3h
3h
≤x≤
2
2
28
REGLA DE LOS TRES OCTAVOS DE
SIMPSON (5)
Se puede calcular el área buscada mediante la expresión:
3h
2
I = ∫ 3h
−
2
3h
 a x 4 bx 3 c x 2
2
a x + b x + c x + d dx = 
+
+
+ d x =
3
2
 4
 − 32h
(
3
2
)
34 ah 4 33 bh 3 32 ch 2 3d h 34 ah 4 33 bh 3 32 ch 2 3d h
=
+
+ 3 +
−
+
− 3 +
=
4.2 4
3.2 3
2
2
4.2 4
3.23
2
2
de donde:
I
=
2.33 bh 3 2.3d h
+
3.23
2
REGLA DE LOS TRES OCTAVOS DE
SIMPSON (6)
Y, realizando las operaciones indicadas, resulta:
32 bh 3
(8.25)
+ 3d h
2
2
Para calcular los valores de las constantes que intervienen en el
3
2
cálculo es necesario hacer:
 3h 
 3h 
 3h 
I=
y0 = a −  + b −  + c −  + d
 2
 2
 2
3
2
 h
 h
 h
y1 = a −  + b −  + c −  + d
 2
 2
 2
3
2
h
h
h
y2 = a  + b  + c  + d
2
2
 
 
 2
3
2
 3h 
 3h 
 3h 
y3 = a  + b  + c  + d
 2
 2
 2
29
REGLA DE LOS TRES OCTAVOS DE
SIMPSON (7)
Resolviendo, por cualquier método, el conjunto de ecuaciones
simultáneas y reemplazando sus valores en la expresión (8.25):
9h 3  2( y0 + y3 ) − 2( y1 + y2 ) 3h
I=

 + [9( y1 + y2 ) − ( y0 + y3 )]
4 
8h 2
 16
de lo que, en definitiva, resulta:
I = ∫ 3 h f ( x )dx =
3h
2
−
2
3h
( y0 + 3 y1 + 3 y2 + y3 )
8
(8.26)
que es la expresión analítica de la denominada REGLA DE LOS
TRES OCTAVOS DE SIMPSON.
REGLA DE LOS TRES OCTAVOS DE
SIMPSON (8)
Al quitarle tres franjas a una zonificación dada por una cantidad
impar de ellas, da como resultado una cantidad par, a la que puede
aplicarse la fórmula de SIMPSON ya estudiada.
Por ejemplo, si se estuviera frente al problema de calcular el área
subdividida en 47 franjas, la REGLA DE LOS TRES OCTAVOS DE
SIMPSON se podría utilizar para aproximar el área bajo la curva
ocupada por las tres primeras franjas. El área bajo las 44 franjas
restantes, luego de ser calculada mediante la fórmula de Simpson, se
sumaría a la de las tres anteriores.
30
FORMULA DE EULER-MACLAURIN
Mediante el agregado de términos complementarios que corrigen
otras fórmulas elementales como la de los TRAPECIOS o SIMPSON,
es posible obtener un sin número de expresiones elementales de
fórmulas de integración.
Una de las más comunes es la que muestra a continuación. La
misma propone adicionar una serie de términos a la fórmula de los
TRAPECIOS, aumentando de este modo, su precisión.
∫
xn
x0
f (x )dx ≅
h
( y 0 + 2 y1 +K+ 2 y n−1 + y n )
2
FORMULA DE EULER-MACLAURIN (2)
Considérese que F(x) es una primitiva de f(x); vale decir que,
F’(x)=f(x), del mismo modo que, F”(x)=f’(x); etc.
Aplicando la fórmula del desarrollo en serie de TAYLOR a la
función primitiva F, resulta:
F (x + h ) = F (x ) + hF ′(x ) +
h2
h3
′
′
F ( x ) + F ′′′(x ) +K
2!
3!
31
FORMULA DE EULER-MACLAURIN (3)
Transponiendo el primer término del segundo miembro, al primer
miembro y tomando, sucesivamente, x=x0 ; x=x1 ; ...; x=xn-1 , resulta:
M
F (x1 ) − F (x0 ) = h f ( x0 ) +
h2
h3
f ′( x0 ) +
f ′′( xo ) +K
2!
3!
F (x2 ) − F ( x1 ) = h f ( x1 ) +
h2
h3
f ′( x1 ) +
f ′′( x1 ) +K
2!
3!
M
M
M
M
2
h
h3
F (xn ) − F (xn −1 ) = h f (xn −1 ) +
f ′(xn −1 ) +
f ′′(xn −1 ) +K
2!
3!
FORMULA DE EULER-MACLAURIN (4)
La suma miembro a miembro de estas ecuaciones da como resultado
en el primer miembro F(xn )-F(x0 ), pero, como F(x) es una primitiva
de f(x), es lícito aplicar la Regla de BARROW al primer miembro,
siendo:
∫
xn
x0
n−1
h2 n−1
h3 n−1
f (x)dx = h∑ f (xi ) + ∑ f ′(xi ) + ∑ f ′′(xi ) +K
2! i =0
3! i =0
i =0
(8.27)
32
FORMULA DE EULER-MACLAURIN (5)
Expresiones análogas a la anterior se obtienen considerando,
sucesivamente, las funciones f ’(x); f ”(x); etc., resultando:
∫
xn
∫
xn
∫
xn
x0
x0
x0
n −1
f ′(x )dx = f ( xn ) − f (x0 ) = h∑
i =0
h 2 n −1
f ′(xi ) + ∑ f ′′(xi ) +K (8.28)
2! i =0
n −1
f ′′( x )dx = f ′( xn ) − f ′( x0 ) = h ∑ f ′′( xi ) +
i =0
n −1
f ′′′(x )dx = f ′′(xn ) − f ′′( x0 ) = h∑ f ′′′( xi ) +
i =0
h 2 n −1
∑ f ′′′(xi ) +K
2! i =0
h 2 n −1 IV
∑ f (xi ) +K
2! i =0
(8.29)
(8.30)
FORMULA DE EULER-MACLAURIN (6)
Sumando a la expresión (8.27) la (8.28) multiplicada por C1 h; la (8.29)
multiplicada por C2 h2; la (8.30) multiplicada por C3 h3, etc., se obtiene:
∫ f (x )dx + C h[ f (x ) − f (x )] + C h [ f ′(x ) − f ′(x )] + C h [ f ′′(x ) − f ′′(x )] +K =
xn
x0
2
1
n
0
2
3
n
0
3
n
0
n −1
n −1
n −1
1

1 C

= h∑ f ( xi ) + h 2 ∑ f ′( xi ) + C1  + h 3 ∑ f ′′( xi ) + 1 + C2  +
2
!
3
!
2
!




i =0
i =0
i =0
n −1
1 C C

+ h 4 ∑ f ′′′( xi ) + 1 + 2 + C3  +K
 4! 3! 2!

i =0
33
FORMULA DE EULER-MACLAURIN (7)
Es necesario determinar ahora, los valores que deben tomar los
coeficientes Ci de modo que se anulen los corchetes que figuran en el
segundo miembro. En consecuencia, se obtiene:
1
1
C1 = −
+ C1 = 0
⇒
2
2!
1
1 C1
C2 =
⇒
+ + C2 = 0
12
3! 2!
1 C1 C2
+ +
+ C3 = 0
4! 3! 2!
⇒
C3 = 0
⇒
.............
1
C4 = −
720
..........................
1 C1 C2 C3
+ +
+
+ C4 = 0
5! 4! 3! 2!
FORMULA DE EULER-MACLAURIN (8)
Así siguiendo se calculan los demás coeficientes.
Sustituyendo estos valores en la última expresión de la integral, se
obtiene la FORMULA DE EULER-MACLAURIN:
1 xn
1
1

f (x )dx =  f (x0 ) + f (x1 ) +K+ f (xn −1 ) − f (xn ) −
∫
h x0
2
2

−
3
h
[ f ′(xn ) − f ′(x0 )] + h [ f ′′′(xn ) − f ′′′(x0 )] −
12
720
−
[
]
h5
f V (xn ) − f V ( x0 ) +K
30240
(8.31)
34
FORMULA DE GREGORY
Una fórmula que utiliza solamente los valores de la función y de las
correspondientes diferencias sucesivas, interiores al intervalo (x0 ; xn)
es la denominada FORMULA DE GREGORY, la cual
será deducida a partir de la ya estudiada expresión de EULERMACLAURYN.
FORMULA DE GREGORY (2)
Si en la citada fórmula, las derivadas son reemplazadas por las
expresiones correspondientes en términos de las diferencias; que son:
1
1
1
h f ′( x0 ) = ∆f (x0 ) − ∆2 f ( x0 ) + ∆3 f ( x0 ) − ∆4 f ( x0 ) +K
2
3
4
1
1
1
h f ′( xn ) = ∇f (xn ) + ∇ 2 f (xn ) + ∇ 3 f (xn ) + ∇ 4 f (xn ) +K
2
3
4
35
FORMULA DE GREGORY (3)
3
7
h 3 f ′′′(x0 ) = ∆3 f (x0 ) − ∆4 f (x0 ) + ∆5 f ( x0 ) −K
2
4
3
7
h 3 f ′′′( xn ) = ∇ 3 f ( xn ) + ∇ 4 f ( xn ) + ∇ 5 f ( xn ) +K
2
4
5
h 5 f V ( x0 ) = ∆5 f ( x0 ) − ∆6 f ( x0 ) +K
2
5
h 5 f V ( xn ) = ∇ 5 f (xn ) + ∇ 6 f ( xn ) +K
2
FORMULA DE GREGORY (4)
Resulta la FORMULA de GREGORY:
1 xn
1
1

f ( x )dx =  f (x0 ) + f ( x1 ) +K+ f ( xn −1 ) + f ( xn ) −
∫
h x0
2
2

−
[
]
1
[∇f (xn ) − ∆f (x0 )] − 1 ∇ 2 f (xn ) − ∆2 f (x0 ) −
12
24
−
[
]
[
]
19 3
3
∇ f (xn ) − ∆3 f (x0 ) −
∇ 4 f (xn ) − ∆4 f ( x0 ) −
720
360
−
[
]
863
∇ 5 f (xn ) − ∆5 f (x0 ) −K
60480
36
METODOS COMBINADOS
•En algunas ocasiones resulta interesante combinar algunos de los
métodos analizados anteriormente para resolver satisfactoriamente
algunos problemas.
•Supongamos dada f(x) en un intervalo (a,b) Cerrado, sobre el cual se
desea obtener la integral de dicha función. Supóngase también que se
dispone de 5 segmentos de recta.
•Una opción seria aplicar el método de Trapecios. No obstante debido al
enorme error por Truncamiento resulta aconsejable combinar las reglas
de Simpson de 1/3 y 3/8 para atacar el problema. Así la regla de
Simpson 1/3 seria aplicada a los dos 1eros segmentos ( 3 puntos )
mientras que para los otros 3 segmentos restantes se recurre a la regla de
Simpson 3/8. Así se obtiene una estimación del error de tercer orden
para todo el intervalo.
METODOS COMBINADOS
Ejercicio: Aplicar esta idea para calcular la integral de la función:
f(x) = 300 x5 – 800 x4+ 600 x3 – 200 x2 + 25 x – 0.2 sobre el intervalo
( 0.05, 0.25) con 5 segmentos sobre dicho intervalo. Efectuar un análisis
comparativo y analizar el error aplicando distintos métodos.
Ejercicio: Aplicar a un ej. practico formulas de trapecios, Euler Mac
Laurin y Gregory, comparar resultados y extraer conclusiones.
37