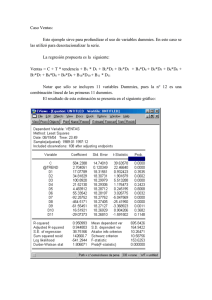
Evaluación numérica de la afirmación de Shapiro. ) )( )) ) = ( ( 1 – ( +

Evaluación numérica de la afirmación de Shapiro.
por
Myron W. Evans,
H. M. Civil List
(www.aias.us, www.atomicprecision.com, www.upitec.org, www.et3m.net)
La correcta evaluación de la afirmación de Shapiro es como sigue:
Definimos en primer lugar:
݂ (‫ ( = )ݎ‬1 –
௥బ -1
௥
) (1 – ( 1 – బ
௥
௥
)(
ோబ మ
௥మ
ି½
))
(1)
.
La demora de tiempo es:
∆‫ݐ = ݐ‬ଷ – ‫ݐ‬଴ ,
(2)
donde
‫ݐ‬ଷ =
‫ݐ‬଴ =
=
ଶ
ோ
ோ
బ
బ
( ‫׬‬ோ ಶ ݂ (‫ ݎ݀ )ݎ‬+ ‫׬‬ோ ು ݂ (‫) ݎ݀ )ݎ‬
௖
ଶ
௖
ଶ
௖
(
ோಶ
‫׬‬ோ ( 1 –
బ
(‫ݎ‬ଵ +
‫ݎ‬ଶ )
(
ோబ మ
௥మ
))
−½
݀‫ ݎ‬+
ଶ
௖
(
(3)
ோು
‫׬‬ோ ( 1 –
బ
.
(
ோబ మ
௥మ
) )−½ ݀‫ݎ‬
(4)
Wald, en su ecuación (6.3.45) ofrece una expresión para ∆‫ ݐ‬. En primer lugar, nótese que
la notación de Wald es:
M (Wald )
ெீ
௖మ
(S.I.)
(5)
De manera que Wald da, en unidades S.I.:
∆‫= ݐ‬
ଶ
[
(ܴா ଶ – ܴ଴ଶ )½ + (ܴ௉ ଶ – ܴ଴ଶ )½ ]
௖
+
ଶெீ
௖య
[ 2 loge (
ோಶ ା(ோಶ మ – ோబ మ )½
ோబ
)
+ 2 loge (
+(
ோು ା(ோು మ – ோబ మ )½
ோబ
ோಶ – ோబ
ோಶ ା ோబ
½
)
+
(
ோು – ோబ
ோು ା ோబ
)
½
)
]
.
(6)
La primera parte de la Ec.(6) es nuestra Ec.(4):
‫ݐ‬଴ =
ଶ
௖
(‫ݎ‬ଵ +
‫ݎ‬ଶ ) =
ଶ
௖
[(ܴா ଶ – ܴ଴ଶ )½ + (ܴ௉ ଶ – ܴ଴ଶ )½ ]
,
(7)
La cual se obtiene analíticamente a partir de la condición:
௥బ
ோబ
=0.
(8)
Es importante notar que tanto Shapiro como Wald dan a ∆‫ ݐ‬como una expresión que agrega
a ‫ݐ‬଴ , es decir,
∆‫( ݐ‬Wald) = ‫ݐ‬଴ + ‫ݐ‬ଷ
(9)
De manera que la así llamada “demora de tiempo” es en realidad un incremento de tiempo.
Por lo tanto, la afirmación de Shapiro repetida por Wald es:
‫ݐ‬ଷ =
ଶெீ
௖య
+
మ
[2 loge ( ோಶା(ோಶோ – ோబ
మ )½
)
బ
2 loge (
+ (
ோು ା(ோು మ – ோబ మ )½
ோಶ – ோబ
ோಶ ା ோబ
ோబ
½
)
+
(
ோು – ோబ
ோು ା ோబ
)
½
)
].
Comprobar :
Esto es para evaluar numéricamente la Ec.(3) con precisión de máquina, y comparar el
resultado con la Ec. (10).
(10)
Parámetros de alimentación:
Estos son ‫ݎ‬଴ , ܴ଴ , ܴா y ܴ௉ , pero para propósitos numéricos, cualquier valor de parámetros
de alimentación pueden emplearse. Utilizar:
MG = 1.327581035 x 1020 m3 s-2
ܿ = 2.997925 x 108 m s-1
de manera que
ଶெீ
௖య
= 9.8543672 x 10-6 s
= 9.8543672 microsegundos.