PRACTICA No

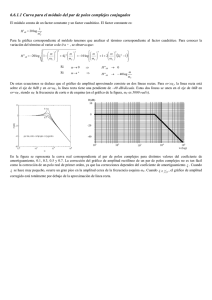
UABC
MODELADO DE SISTEMAS DINÁMICOS
RESPUESTA A LA FRECUENCIA
DIAGRAMAS DE BODE
INTRODUCCION
Sea H (s) cualquier función de red ó de transferencia. Para obtener su
respuesta a la frecuencia hacemos s = jω y obtenemos H (jω), la cual es
una función compleja que se puede expresar, ya sea en coordenadas
rectangulares o en coordenadas polares, de la siguiente forma:
H ( jω ) = A( jω ) + jB ( jω ) = H ( jω ) e j φ (ω )
donde:
A(ω ) = Re H ( jω )
B (ω ) = Im H ( jω )
H ( jω ) =
A( jω ) 2 + B ( jω ) 2 = Magnitud
H ( jω ) dB = 20 log H ( jω ) = Magnitud en decibeles
B (ω )
= ∠H ( jω ) = Fase en grados
A(ω )
El parámetro de Magnitud en un diagrama de Bode se expresa en
unidades de decibeles. Puesto que se emplean logaritmos se deben
aplicar sus propiedades; es decir, los productos se convierten es sumas y
las divisiones se convierten en restas.
El parámetro de Fase se expresa ya sea en grados, o bien en radianes y
se realiza una conversión entre ambos mediante la siguiente regla de
tres:
π rad . ___ 180 o
φ (ω ) = tg −1
2π rad . __ 360 o
1 rad . = 57.3o
Cuando se obtiene la cantidad de grados en una función de transferencia
los ángulos se suman en los productos y se restan en las divisiones.
Para graficar un diagrama de Bode se pueden emplear las siguientes
definiciones:
Si se emplean octavas:
• ω2 está una octava arriba de ω1 si ω2 = 2ω1.
• ω2 está una octava abajo de ω1 si ω2 = ω1/2.
Si se emplean décadas:
Pag. 1
UABC
•
•
MODELADO DE SISTEMAS DINÁMICOS
ω2 está una década arriba de ω1 si ω2 = 10ω1.
ω2 está una octava abajo de ω1 si ω2 = ω1/10.
Los posibles factores que se presentan en una función de transferencia
son:
• Constante K
Magnitud
dB
20 log K
log ω
Fase
∠φ
K >0
0o
− 180 o
log ω
K <0
Obsérvese que si K es un número positivo entonces en la fase habrán
cero grados.
Si K es un número negativo entonces en la fase habrán -180 grados.
¡¡¡No se confunda esto con el valor positivo ó negativo que se podría
obtener al calcular 20 log K en decibeles!!!.
Pag. 2
UABC
•
MODELADO DE SISTEMAS DINÁMICOS
1
) y Ceros en el origen ( s m )
m
s
Polos en el origen (
Magnitud
H ( jω ) dB
sm
m = 1,2,...
20
10 −1 10 0
− 20
101
dB
dec.
10 2
dB
dec.
log ω
m = 1,2,...
1
sm
Fase
∠H ( j ω )
180 o
m=2
s2
90 o
m =1
s1
log ω
− 90 o
m =1
− 180 o
m=2
1
s1
1
s2
El exponente m representa el número de polos ó ceros en el origen. Si
m>1, solo aparecerá un conjunto de gráficas encimadas en la magnitud y
cuando se efectúe la suma de logaritmos se multiplicará por m.
Sin embargo, en la fase se puede apreciar las diferencias, por ejemplo,
cuando m=2 la fase será igual a 180° si se trata de un cero en el origen, o
bien -180° si se trata de un polo en el origen.
Pag. 3
UABC
Polos reales (
MODELADO DE SISTEMAS DINÁMICOS
1
1+
s
p
) y Ceros reales ( 1 +
s
)
z
Magnitud
1+
H ( jω ) dB
20
s
z
dB
década
z
log ω
p
1
− 20
dB
década
1+
s
p
Fase
∠H ( j ω )
1+
90 o
s
z
45 o
0.1z
0.1 p
z
p
10 z
10 p
log ω
− 45 o
− 90 o
1
1+
s
p
Obsérvese que la frecuencia del polo y del cero se ubican en ±45 según
sea el caso, además, inicia una década abajo de su frecuencia y se
termina en una década arriba fijándose finalmente en ±90, según sea el
caso.
Pag. 4
UABC
MODELADO DE SISTEMAS DINÁMICOS
Polos complejos (
1+
1
2ςs
ωn
+
s2
) y Ceros complejos ( 1 +
2ςs
ωn
s2
+
ω n2
ω n2
)
Magnitud
1+
H ( jω ) dB
40
2ς s
ωn
+
s2
ω n2
dB
década
log ω
ωn
− 40
dB
década
1+
1
2ς s
ωn
+
s2
ω n2
Fase
∠H ( jω )
180o
1+
2ς s
ωn
+
s2
ω n2
90 o
0.1ω n
ωn
log ω
10ω n
− 90 o
− 180o
1+
1
2ς s
ωn
+
s2
ω n2
Obsérvese que la diferencia de una raíz simple de una compleja es que la Magnitud varía
20 decibeles más en una raíz compleja comparada con una simple.
Obsérvese que la diferencia de una raíz simple de una compleja es que la Fase varía 45
grados más en una raíz compleja comparada con una simple.
Pag. 5