Examen Final (01 de febrero de 2016) 2. Sistemas de Ecuaciones

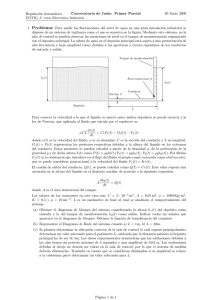
Ecuaciones Diferenciales y Métodos Numéricos (MUII).
Examen Final
Curso 2015-16.
(01 de febrero de 2016)
2. Sistemas de Ecuaciones Diferenciales Ordinarias.
1. Dos depósitos, de 6 m3 de capacidad, están interconectados entre sı́ y con el exterior según
la siguiente figura:
16 m3 /dı́a
?
18 m3 /dı́a
1
2
2 m3 /dı́a
16 m3 /dı́a
?
Las velocidades representadas en la figura son las del agua que fluye continuamente por el
sistema.
a) Supongamos que inicialmente se depositan 20 kg de sal en el primer depósito y 10 kg en
el segundo. El agua que entra del exterior en el segundo depósito tiene una concentración
de sal de C kg/m3 . ¿Cuánto tiene que valer C para que al cabo de 1 dı́a en el primer
depósito haya 25.72115605893691 Kg de sal?
b) Si la concentración de sal C cambia periódicamente, C(t) = 5 − sen(t), ¿qué ocurrirá a
largo plazo en el sistema?
c) Suponiendo las condiciones iniciales del primer apartado y los depósitos llenos, si no
hay entrada de agua en el segundo depósito ¿cuánta sal quedará en cada uno de los
depósitos 6 horas después? (Nota: El sistema deja de ser autónomo)
2. Dado el siguiente sistema:

4
x0 =  −5
3


5
6
−6 −6  x + b(t)
3
2

0
a) Para b(t) =  0  encuentra su solución general y la solución particular para las
0


0
condiciones iniciales x(0) =  1 .
−1


0
b) Para b(t) =  −1 , calcula el equilibrio del sistema y encuentra su solución general.
1
¿Qué forma tienen las condiciones iniciales de las soluciones que convergen hacia el
equilibrio?


0
c) Para b(t) =  3e−2t , encuentra su solución general y las condiciones iniciales de
e−2t
todas las soluciones que convergen hacia cero. ¿Tiene algún equilibrio el sistema?
3. Dado el siguiente sistema:
(
x0 = 2x − x2 − xy
y 0 = −y + xy
a) Encuentra sus equilibrios y estudia su estabilidad.
b) En el plano de fases del sistema dibuja las órbitas correspondientes a los equilibrios y
a las soluciones de la forma (0, y(t)) y (x(t), 0). Ayúdate de Maxima para completar
el diagrama de fases. ¿Cuál es el comportamiento a largo plazo de las soluciones con
condiciones iniciales positivas?
La duración del examen es de 2 horas.
Cada uno de los 8 apartados que hay entre los tres problemas puntúa sobre 0.5.