condensadores y dielectricos - Actiweb crear paginas web gratis

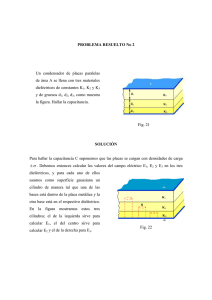
Cap. 6: Condensadores y dieléctricos 144
Apuntes de física II
Capítulo 6.
CONDENSADORES Y DIELECTRICOS
6.1 INTRODUCCION.
Un caso especial importante se presenta en la práctica cuando dos conductores próximos reciben cargas del
mismo valor y signos opuestos. Este dispositivo de dos conductores se denomina condensador.
En la figura 6.1 se muestra el caso más general de un condensador formado por dos conductores cercanos,
a los cuales se les llama placas. Las cargas iguales y opuestas se obtienen conectando las placas
momentáneamente a los polos opuestos de una batería.
Figura 6.1
La capacitancia C de cualquier condensador como el de la figura 6.1 se define como
C=
q
V
6.1
en la cual V es la diferencia de potencial entre las placas y q es la magnitud de la carga en cualquiera de las
placas; q no debe considerarse como la carga neta del condensador, la cual es cero. La capacitancia de un
condensador depende de la forma geométrica de cada placa, de la relación espacial entre ellas, y del medio
en el cual están sumergidas. De momento, se considera a este medio como el vacío.
La unidad de capacitancia se define de la ecuación 6.1 que es el coulombio/voltio que en el sistema SI es el
faradio, en honor a Michael Faraday:
[capaci tan cia ] = 1F = 1C
1V
El faradio es una unidad de capacitancia muy grande, en la práctica son unidades más convenientes los
submúltiplos del faradio, el microfaradio ( 1µF
( 1µµF
= 10 −6 F
) y el micromicrofaradio o picofaradio
= 10 −12 F = 1 pF ).
Un condensador se representa por el símbolo
.
6.2 CALCULO DE LA CAPACITANCIA.
Apuntes de física II
[email protected]
Cap. 6: Condensadores y dieléctricos 145
Apuntes de física II
La figura 6.2 muestra un condensador formado por dos placas planas paralelas de área A, separadas por una distancia
pequeña d comparada con las dimensiones lineales de las placas. Prácticamente, todo el campo de este condensador está
v
localizado en el espacio comprendido entre las placas, como se representa en la figura. El campo eléctrico E a medida
que d es mucho menor que las dimensiones de las placas es uniforme, lo que quiere decir que las líneas de fuerza son
paralelas y están uniformemente espaciadas. Para el efecto de los cálculos las “deformaciones” de las líneas en los bordes
se pueden pasar por alto.
Figura 6.2
Para el cálculo de la capacitancia se supone que el condensador ha sido conectado a los bornes de una batería, de tal
manera que, hay una carga +q en una placa y una carga –q en la otra.
v
En el siguiente paso se calcula el campo eléctrico E entre las placas usando la ley de Gauss. La figura 6.2 muestra con
líneas interrumpidas una superficie gaussiana con el tamaño y forma de las placas del condensador. El flujo neto es
v
q
∫ E.nˆdA = EA = ε
E=
entonces,
0
q
ε0 A
Que es el campo debido a la cara de la superficie gaussiana que está entre las placas; en esa región
v
v
E
es constante.
v
En las otras superficies el flujo de E es cero, pues una de ellas está dentro del conductor y el campo eléctrico E dentro
de un conductor con carga estática es cero. En las otras cuatro superficies es cero porque, si no se tienen en cuenta las
v
irregularidades de las líneas de fuerza en los bordes, el campo E es normal a las superficies.
En el siguiente paso se calcula el trabajo por unidad de carga para llevar una carga de prueba de una placa a la otra, o sea,
v v
V = − ∫ E ⋅ dl ,
siendo V la diferencia de potencial entre las placas. La integral se realiza entre la placa inferior y la superior donde
v v
E ⋅ dl = − Edl
por ser antiparalelos, de modo que
s
V = ∫ Edl = Ed =
i
q
d
ε0A
De acuerdo a la ecuación 6.1 la capacitancia de este condensador es
C=
La ecuación 6.2 sugiere unidades para la constante de permitividad
ε0
q ε0 A
=
V
d
6.2
que son más apropiadas para los problemas en los
que intervienen condensadores, es decir,
Apuntes de física II
[email protected]
Cap. 6: Condensadores y dieléctricos 146
Apuntes de física II
ε 0 = 8.85 × 10 −12 Fm −1 = 8.85 pFm −1
Las unidades usadas en la ley de Coulomb son equivalentes a las usadas acá.
Ejemplo 1. las placas de un condensador de placas paralelas están separadas una distancia d=1.0mm. ¿Cuál debe ser el
área de cada placa si la capacitancia es de 1F?.
De la ecuación 6.2 se despeja A y se obtiene
A=
Cd
ε0
(1F )(1.0 × 10 −3 m)
= 1.1 × 10 8 m 2
=
−12
−1
8.85 × 10 Fm
Esto corresponde a un cuadrado de aproximadamente 10km de lado. Por eso el faradio es una unidad muy grande. La
tecnología actual hace posible construir “supercondensadores” de 1F de pocos centímetros de lado, que se usan como
fuentes de voltaje para computadoras; como soporte para mantener la memoria de los computadores cuando hay una falla
de energía bastante prolongada (Aproximadamente 30 días).
Ejemplo 2. Un condensador cilíndrico está formado por un cilindro y un cascaron cilíndrico coaxial de radios a y b
respectivamente y longitud l como se muestra en la figura 6.3. ¿Cuál es la capacitancia de este aparato?.
Con
l ⟩⟩ a y b
de modo que se puedan pasar por alto las irregularidades de las líneas de fuerza en los extremos del
condensador.
Como superficie gaussiana se construye un cilindro coaxial de radio r y longitud l, cerrado por tapas paralelas planas como
en la figura 6.3 b).
Figura 6.3
Aplicando la ley de Gauss se tiene
v
ε 0 ∫ E ⋅ nˆ dA = q
ε 0 E (2π rl ) = q
Que es el flujo neto a través de la superficie gaussiana. El flujo está totalmente a través de la superficie cilíndrica y no a
través de las tapas extremas. Despejando a E se obtiene:
E=
q
2πε 0 rl
La diferencia de potencial entre las placas es
Apuntes de física II
[email protected]
Cap. 6: Condensadores y dieléctricos 147
Apuntes de física II
v
b v
b
b
V = − ∫ E ⋅ dl = ∫ Edr = ∫
a
a
a
q
dr
q
b
=
ln
2πε 0 l r
2πε 0 l a
Finalmente, la capacitancia está dada por
C=
2πε 0 l
q
=
V ln(b a)
De nuevo la capacitancia depende de factores geométricos y de la permitividad entre las placas.
Ejercicio. Muestre que si la distancia entre los cilindros, b-a, es muy pequeña comparada con a, la formula se reduce a la
que se había podido obtener utilizando la ecuación 6.2.
Use la expansión en series de Ln(1+x), con x=(b-a)/a.
6.3 CONDENSADORES EN SERIE Y EN PARALELO.
Los condensadores se pueden combinar de dos maneras: en serie y en paralelo.
a) Condensadores en paralelo. La figura 6.4 muestra tres condensadores en paralelo y se trata de hallar la capacitancia
equivalente de ese sistema. Para esa configuración la diferencia de potencial entre los puntos a y b es la misma.
Figura 6.4
Todas las placas superiores están conectadas entre sí y a la terminal a, mientras que todas las placas inferiores están
conectadas entre si y con la terminal b. La capacitancia equivalente de un conjunto de condensadores conectados entre sí
es la capacidad de un único condensador que cuando sustituye al conjunto produce el mismo efecto exterior.
Aplicando la relación q=CV a cada condensador se obtiene:
q1 = C1V ;
q 2 = C 2V ;
y
q3 = C 3V
La carga total en la combinación es:
q = q1 + q 2 + q3 = (C1 + C 2 + C 3 )V .
La capacitancia equivalente C es:
C eq = C1 + C 2 + C 3
6.3
Este resultado puede generalizarse fácilmente a un número cualquiera de condensadores conectados en paralelo así:
n
C eq = ∑ C i
6.4
i =1
b) Condensadores en serie.
La figura 6.5 muestra tres condensadores conectados en serie. Para condensadores como se muestra, la magnitud de la
carga q en cada placa debe ser la misma. Así debe ser porque la carga neta en la parte del circuito encerrada por la línea
Apuntes de física II
[email protected]
Cap. 6: Condensadores y dieléctricos 148
Apuntes de física II
interrumpida en la figura 6.5 a) debe ser cero; esto es, la carga existente en estas placas inicialmente es cero, y el conectar
una batería entre a y b sólo da lugar a una separación de cargas, la carga en estas placas sigue siendo cero.
Figura 6.5
La diferencia de potencial entre los extremos de un cierto número de condensadores conectados en serie es la suma de las
diferencias de potencial entre los extremos de cada condensador individual.
Aplicando la ecuación
V =q C
a cada condensador se obtiene:
V1 =
q
;
C1
V2 =
q
;
C2
V3 =
y
q
C3
⎛ 1
1
1 ⎞
⎟⎟ .
+
V = V1 + V2 + V3 = q⎜⎜ +
C
C
C
2
3 ⎠
⎝ 1
La capacitancia equivalente es:
C=
q
1
=
1
1
1
V
+
+
C1 C 2 C3
1
1
1
1
=
+
+
C eq C1 C 2 C3
6.5
La capacitancia equivalente en serie es siempre menor que la más pequeña de las capacitancias de la conexión.
Este resultado puede generalizarse fácilmente a un número cualquiera de condensadores conectados en serie así:
n
1
1
=∑
C eq i =1 Ci
6.6
Ejemplo 3. En el circuito mostrado en la figura 6.6 los puntos a y b están a una diferencia de potencial de 100voltios y
conformado por los condensadores
C1 = 15µF , C 2 = 3µF , C3 = 6µF y C 4 = 8µF .
a) Hallar la capacitancia
equivalente entre los puntos a y b. b) La carga y la diferencia de potencial a través de cada condensador.
Figura 6.6
a) Para simplificar el circuito y hallar la capacitancia equivalente se utilizan las ecuaciones 6.4 y 6.5 en la siguiente
secuencia a saber.
Apuntes de física II
[email protected]
Cap. 6: Condensadores y dieléctricos 149
Apuntes de física II
1
1
1
;
=
+
C 23 C 2 C 3
C 2 C3
(3µF )(6µF )
C 23 =
=
= 2µF
C 2 + C3
3µF + 6µF
C 234 = C 4 + C 23 = 8µF + 2µF = 10µF
1
C1234
=
C1234 =
1
1
+
;
C1 C 234
C1C 234
(15µF )(10µF )
=
= 6µF
C1 + C 234 15µF + 10µF
b) Para hacer la parte restante, se usa el hecho de que, si se conocen dos cualesquiera de los tres parámetros q, V y C, el
tercero se puede hallar de la ecuación 6.1.
C1234 = 6µF , Vab = 100V .
Entonces, para este condensador equivalente, la
q = C1234Vab = (6µF )(100V ) = 600µC . En 2) los condensadores de 15 µF y 10 µF están
En
3),
tienen la misma carga del condensador equivalente.
carga
es
en serie y
Entonces, la diferencia de potencial para el condensador C1 es
V1 = q C1 = 600µC 15µF = 40V y para el condensador C234 la diferencia de potencial es
V234 = q C 234 = 600µC 10µF = 60V .
En 1), los dos condensadores C 4 = 8µF y C 23 = 2 µF están a la misma diferencia de potencial de 60V. Entonces,
para el condensador de C4 la carga es de q 4 = C 4V234 = (8µF )(60V ) = 480 µC y para el condensador C23 la
carga es q 23 = C 23V234 = ( 2 µF )(60V ) = 120 µC.
En la figura 6.6, los condensadores C2 y C3 tienen la misma carga que C23. Entonces, para el condensador C2 la diferencia
V2 = q 23 C 2 = 120µC 3µF = 40V
C3 = 120µC 6µF = 20V .
de potencial es
V3 = q 23
y para el condensador C3 la diferencia de potencial es
Nota:
1.
2.
Para determinar la capacitancia equivalente, el circuito se simplifica subsecuentemente desde la figura original
hasta 3). Para evitar errores, se dibuja un nuevo diagrama después de cada paso.
En la segunda parte de este problema se comienza con el equivalente 3) y se trabaja hacia atrás hasta la figura
original 6.6. En cada uno de estos pasos se usa ya sea la ecuación 6.4 o la 6.5. Por ejemplo, en 2) los dos
condensadores están en serie y por ello deben tener la misma carga que el condensador equivalente.
Ejemplo 4. Un condensador tiene placas cuadradas, cada una de lado a, y formando un ángulo θ entre sí, como se ve en
la figura 6.7. Encontrar la capacitancia de ese condensador para valores pequeños de θ.
Figura 6.7
Apuntes de física II
[email protected]
Cap. 6: Condensadores y dieléctricos 150
Apuntes de física II
Para resolver este problema se considera un
condensador elemental de longitud dx y de separación h
como se muestra en la figura adjunta.
La capacitancia de ese elemento es, la capacitancia de
un condensador plano dado por:
dC =
ε 0 adx
h
Expresando a h en función de x y de θ como h=d+xtgθ. Los condensadores elementales están en paralelo, por lo tanto la
capacitancia total es la superposición de todas las capacitancias elementales.
Entonces:
C=∫
a cos θ
0
Haciendo
u = d + xtgθ ;
du = tgθdx
C=
ε 0a
dx
d + xtgθ
y remplazando en la ecuación anterior se tiene:
ε 0 a d + asenθ du ε 0 a
[ln(d + asenθ ) − ln d ]
=
tgθ ∫d
u
tgθ
La capacitancia del sistema es:
C=
Si θ es pequeño,
tgθ ≈ senθ = θ .
ε 0 a ⎛ asenθ ⎞
ln⎜1 +
⎟
tgθ ⎝
d ⎠
De donde
C=
ε 0 a ⎛ aθ ⎞
ln⎜1 +
⎟
d ⎠
θ ⎝
Como θ es pequeño, aθ/d es mucho menor que 1. Usando la serie de
ln(1 + x) = x −
x2 x3 x4
+
−
⋅⋅⋅⋅
2
3
4
Tomando los dos primeros términos de la serie en la capacitancia se tiene:
C=
ε 0 a ⎛ aθ a 2 θ 2 ⎞ ε 0 a 2 ⎛ a θ ⎞
⎟=
⎜
−
⎜1 −
⎟
d ⎝ 2d⎠
2 d 2 ⎟⎠
θ ⎜⎝ d
Nótese que el caso limite se obtiene cuando θ=0, que da un condensador plano de superficie A=a y espesor d como la
ecuación 6.2.
2
6.4 DIELECTRICOS.
Hasta ahora, no se ha considerado problemas en los que intervienen medios dieléctricos y se han tratado casos en los
cuales el campo eléctrico es producido exclusivamente por una distribución específica de cargas o por cargas libres sobre la
superficie de los conductores. En esta sección se mejora esta situación considerando el caso más general.
Apuntes de física II
[email protected]
Cap. 6: Condensadores y dieléctricos 151
Apuntes de física II
Un material dieléctrico ideal es aquel que no tiene cargas libres. Sin embargo, todos los medios materiales se componen
de moléculas, estas a su vez se componen de entes cargados (núcleos atómicos y electrones), y las moléculas de los
dieléctricos son, de hecho, afectadas por la presencia de un campo eléctrico. El campo eléctrico produce una fuerza que se
ejerce sobre cada partícula cargada, empujando las cargas positivas en la dirección del campo, y las negativas en sentido
contrario, de modo que las partes positivas y negativas de cada molécula se desplazan de sus posiciones de equilibrio en
sentidos opuestos. Sin embargo, estos desplazamientos del orden de un diámetro molecular están limitados por intensas
fuerzas restauradoras que se forman por el cambio de la configuración de las cargas de la molécula. El termino carga
ligada, en contraste con la carga libre de un conductor, se usa a veces para poner énfasis en el hecho de que tales cargas
moleculares no están libres para moverse muy lejos o ser extraídas del material dieléctrico. El efecto total, desde el punto
de vista microscópico, se visualiza más fácil como un desplazamiento de toda la carga positiva en el dieléctrico en relación
con la carga negativa. Se dice entonces que el dieléctrico está polarizado.
Un dieléctrico polarizado, aun cuando sea eléctricamente neutro en promedio, produce indudablemente un campo eléctrico
en los puntos exteriores e interiores al dieléctrico. Como resultado, existe una situación algo embarazosa: la polarización del
dieléctrico depende del campo eléctrico total del medio, pero una parte del campo eléctrico es producida por el dieléctrico
mismo. Además, el campo eléctrico distante del dieléctrico puede modificar la distribución de carga libre sobre los cuerpos
de los conductores y estos, a su vez, producir modificaciones del campo eléctrico en el dieléctrico.
Cuando se coloca un conductor en un campo eléctrico externo, los electrones libres dentro del mismo experimentan
desplazamientos, como consecuencia de las fuerzas ejercidas sobre ellos por el campo. Se ha visto en capítulos anteriores
que, en el estado de equilibrio final, el conductor tiene una carga inducida sobre su superficie, distribuida de tal modo que el
campo creado por ella neutraliza el campo inicial en todos los puntos interiores, y se reduce a cero el campo eléctrico neto
dentro del conductor.
Ahora se trata de entender, en términos atómicos, lo que ocurre cuando se coloca un dieléctrico en un campo eléctrico.
Las moléculas de un dieléctrico se clasifican en polares y no polares. En una molécula no polar los “centros de gravedad
“de los núcleos positivos y de los electrones coinciden normalmente, mientras que en una molécula polar no coinciden. Las
moléculas simétricas, H2, N2 y 02, son no polares. Por el contrario, en las moléculas, N20 y H20, ambos átomos de nitrógeno
o de hidrogeno se encuentran a un mismo lado del átomo de oxigeno; tales moléculas son polares.
Bajo la influencia de un campo eléctrico, las cargas de una molécula no polar llegan a desplazarse, como se muestra en la
figura 6.8 b).
Figura 6.8
En este caso las moléculas se han polarizado por el campo y los dipolos que resultan se les denominan dipolos inducidos.
Cuando una molécula no polar se polariza, sobre las cargas desplazadas entran en juego fuerzas recuperadoras, que
tienden a juntarlas como si estuvieran unidas por un resorte. Bajo la influencia de un campo exterior dado, las cargas se
separan hasta que la fuerza recuperadora es igual y opuesta a la ejercida por el campo sobre ellas. Naturalmente, las
fuerzas recuperadoras varían en magnitud de un tipo a otro de molécula, con las consiguientes diferencias de
desplazamiento para un campo dado.
Si un dieléctrico se compone de moléculas polares o dipolos permanentes, estos están orientados al azar cuando no existe
campo eléctrico, tal como se indica en la figura 6.9 a).
Figura 6.9
v
Bajo la acción de un campo eléctrico E , se produce cierto grado de orientación y, cuanto más intenso es el campo, tanto
mayor es el número de dipolos que se orientan en la dirección del mismo, como se representa en la figura 6.9 b).
Sean o no polares las moléculas de un dieléctrico, el efecto neto de un campo exterior es en definitiva el mismo que el
representado en la figura 6.10.
Apuntes de física II
[email protected]
Cap. 6: Condensadores y dieléctricos 152
Apuntes de física II
Figura 6.10
Dentro de las dos capas superficiales extremadamente delgadas, indicadas por las líneas de trazos, hay un exceso de
carga, negativa en una y positiva en la otra. Estas capas de carga son las que dan origen a la carga inducida sobre las
superficies de un dieléctrico. Las cargas no son libres, sino que cada una está ligada a una molécula situada en la
superficie, o próxima a ella. Dentro del resto del dieléctrico, la carga neta por unidad de volumen sigue siendo nula. El
material como un todo se convierte en un gran dipolo eléctrico que tiende a moverse en la dirección en que aumenta el
campo eléctrico.
6.5 POLARIZACION.
v
La polarización P de un material es una cantidad vectorial definida como el momento dipolar eléctrico del
v
material por unidad de volumen. Por lo tanto, si p es el momento dipolar inducido en cada átomo o
molécula y n el número de átomos o moléculas por unidad de volumen, la polarización es
v
En general la polarización P
v
v
P = np
6.7
tiene la misma dirección que el campo eléctrico aplicado.
Para el caso especial de la figura 6.10, el vector polarización
v
P
tiene el mismo valor en todos los puntos del
dieléctrico; en otros casos, puede variar de un punto a otro, y entonces las magnitudes n y
v
v
p se refieren a
un volumen muy pequeño que incluye el punto. La polarización P , como un momento dipolar eléctrico por
unidad de volumen, se mide en (Cm)m-3 o Cm-2, que corresponde a una carga por unidad de área.
Se definió en un capitulo anterior que el momento dipolar de un dipolo era el producto de cualquiera de las
cargas que forman el dipolo por la distancia que las separa. El bloque polarizado de la figura 6.10 se
considera como un gran dipolo único, formado por las cargas inducidas
qp = σ p A,
separadas por el
p = q p L = σ p AL , y, dado
v
volumen es AL, el momento dipolar por unidad de volumen, o polarización P , vale en magnitud
espesor L del bloque.
El momento dipolar del bloque es entonces
P=
σ p AL
σ p AL
=
=σp
Volumen
AL
que su
6.7
La densidad superficial de carga ligada es igual a la polarización. Aunque este resultado se ha obtenido para
una configuración geométrica particular, su validez es general y para otra configuración la densidad de carga
de polarización está dada por
v
σ p = P ⋅ nˆ = P cosθ
6.8
Donde θ es el ángulo formado por el vector normal a la superficie y el vector polarización.
Ejemplo 5. Una varilla delgada de dieléctrico de sección transversal A se coloca sobre el eje x, desde x=0
hasta x=L como se muestra en la figura 6.11. El vector polarización es a lo largo de su longitud, y está dada
por
v
P = ( ax 2 + b)uˆ x
Apuntes de física II
. Hallar la densidad superficial de carga de polarización, en cada extremo.
[email protected]
Cap. 6: Condensadores y dieléctricos 153
Apuntes de física II
Figura 6.11
Para la solución de este problema se usa la ecuación 6.8.
Como primer paso se calcula el vector polarización en cada una de las caras de la varilla, a saber:
v
P1 = buˆ x
v
P2 = ( aL2 + b)
Por lo tanto en la cara 1 la densidad superficial de carga es:
v
σ P = P1 ⋅ nˆ1 = P1uˆ x ⋅ nˆ1 = − P1 = −b
1
La carga superficial en 1 es:
q P1 = σ P1 A = − Ab
La densidad de superficial de carga en la superficie 2 es:
v
σ P = P2 ⋅ nˆ 2 = P2 uˆ x ⋅ nˆ 2 = P2 = aL2 + b
2
La carga superficial en 2 es:
q P2 = A(aL2 + b)
6.6 SUCEPTIBILIDAD Y PERMITIVIDAD ELECTRICAS.
v
La polarizacion P de un dieléctrico isótropo homogéneo tiene dirección y sentido iguales que el campo eléctrico
v
v
resultante E , y depende de E y de la naturaleza del dieléctrico. Se define una propiedad del dieléctrico en la teoría de
respuesta lineal, denominada susceptibilidad eléctrica del material
χ e , por la ecuación
v
v
P = ε0χeE
v
La susceptibilidad eléctrica χ e es adimensional puesto que tanto P como
los materiales
χe
v
ε0E
6.9
-2
se miden en Cm . Para la mayoría de
es una cantidad positiva. La susceptibilidad eléctrica del vacío es nula, ya que solo puede resultar
polarizado un material dieléctrico. La susceptibilidad eléctrica, que describe la respuesta de un medio a la acción de un
campo eléctrico, está relacionada con las propiedades de los átomos y moléculas del medio. Por esta razón, la
susceptibilidad eléctrica es diferente para campos eléctricos estáticos y oscilantes. La susceptibilidad eléctrica inducida
debida a la distorsión del movimiento electrónico en átomos o moléculas es esencialmente independiente de la temperatura,
puesto que se trata de un efecto relacionado con la estructura electrónica de los átomos o de las moléculas y no con el
movimiento térmico.
Para un bloque plano como el de la figura 6.10 colocado en un campo eléctrico externo normal a sus caras, la densidad
superficial de carga ligada es igual a la polarizacion; de modo que en este caso
Apuntes de física II
[email protected]
Cap. 6: Condensadores y dieléctricos 154
Apuntes de física II
σ p = ε 0 χ e E.
Si ese bloque dieléctrico se coloca entre las placas de un condensador plano paralelo de área A y separación d como el de
la figura 6.11 el cual inicialmente estaba vacío y con una densidad de carga superficial llamada libre. La densidad de carga
σL
E L = σ L ε 0 cuando no
hay dieléctrico en él, la carga ligada produce un campo eléctrico en sentido contrario el cual es E P = σ P ε 0 cuando el
superficial libre en las placas se denota por
y dentro del condensador produce un campo
condensador se ha llenado con el material dieléctrico.
Figura 6.11
El campo resultante
v v
v
E = E L + E P . Dado que estos campos tienen sentidos opuestos como en la figura 6.11, el campo
resultante E es:
E = EL − EP = EL −
χε E
σP
= EL − e 0 = EL − χ e E
ε0
ε0
y, por tanto,
E=
σ
EL
E
= L = L
1+ χe
κ ε 0κ
6.10
ε
ε0
6.11
Donde el coeficiente
κ = 1+ χe =
Es la permitividad relativa y es un número sin unidades. A la permitividad relativa también se le llama la constante
dieléctrica.
Las tres magnitudes
χe , ε y κ
son otras tantas formas diferentes de expresar la misma propiedad
fundamental de un dieléctrico; esto es, el grado en el cual queda polarizado cuando se encuentra en un campo eléctrico.
Cualquiera de ellas puede expresarse en función de
ε 0 y de una de las restantes, y todas se introducen únicamente con el
fin de simplificar la forma que toman algunas ecuaciones de uso frecuente.
Aunque la ecuación 6.10 se dedujo para un caso especial, el resultado anterior tiene validez general cuando se sustituye el
vacío por un dieléctrico homogéneo e isótropo en todos los puntos donde existe campo eléctrico; la intensidad EL en un
punto cualquiera, creada por cargas libres situadas sobre conductores, queda reducida por el factor 1/κ. La presencia del
dieléctrico reduce efectivamente la interacción entre las cargas debido al efecto de pantalla producido por la polarizacion de
las moléculas del dieléctrico.
Ejemplo 6. Una carga puntual q está en el centro de una esfera de material dieléctrico de radio R como la figura 6.12 y
susceptibilidad eléctrica χe=5.
a) Calcular el vector polarizacion en la superficie.
b) Calcular la carga total de polarizacion en la superficie.
Apuntes de física II
[email protected]
Cap. 6: Condensadores y dieléctricos 155
Apuntes de física II
Figura 6.12
a) En la figura 6.12 el campo eléctrico en la superficie es el campo neto dado por la ecuación 6.10, debido a la carga
puntual q y al campo de polarizacion. Este campo es:
v
E=
q
uˆ R
4πε 0κ R 2
1
El vector polarizacion es:
v
v ε χ q
χ q
P = ε 0 χ e E = 0 e 2 uˆ R = e 2 uˆ R
4πε 0κ R
4πκ R
Con
κ = 1+ χe = 6.
Por lo tanto el vector polarización para esta situación es:
v
5 q
uˆ R .
P=
24π R 2
b) La carga de polarizacion inducida en la superficie es:
v
⎛ 5 q ⎞
uˆ R ⎟ ⋅ nˆ r dA
q P = ∫ σ P dA = ∫ P ⋅ nˆ r dA = ∫ ⎜
s
s
s 24π R
⎝
⎠
qP =
5 q
5 q
( 4πR 2 )
dA =
2 ∫s
2
24π R
24π R
qP =
5
q
6
6.7 CONDENSADOR CON DIELECTRICO.
Para el caso de la figura 6.11, donde la carga libre está en la superficie de las placas, el campo eléctrico
entre ellas en el vacío es de acá en adelante
E0 ≡ E L = σ L ε 0
; y la diferencia de potencial,
V0 = E 0 d
Cuando hay dieléctrico en las placas, el campo eléctrico es
E = E 0 κ , y la diferencia de potencial,
V = Ed =
Apuntes de física II
E0
κ
d=
V0
κ
6.12
[email protected]
Cap. 6: Condensadores y dieléctricos 156
Apuntes de física II
Como
κ ⟩ 1 , la diferencia de potencial V es menor que V .
0
Las cargas inducidas sobre el dieléctrico debilitan
el campo entre las placas, reduciendo la diferencia de potencial.
La capacidad de un condensador en el vacío, con una carga qL sobre las placas, es
C0 =
qL
V0
Cuando entre ellas se introduce un dieléctrico,
C=
qL
q
q
= L = Lκ
V V0 κ V0
C = κC 0
6.13
Es decir, la capacitancia aumenta en el factor κ cuando el dieléctrico llena por completo la región entre las
placas.
Para un condensador de placas paralelas, donde
C0 = ε 0 A d
ecuación 6.2, se puede expresar la
capacitancia, cuando el condensador está lleno con un dieléctrico, como
C =κ
ε0 A
d
=
εA
6.14
d
La ecuación 6.2 es un caso especial de esta relación que se obtiene al poner κ = 1 , y que corresponde al
caso de vacío entre las placas. Así pues, la capacitancia de cualquier condensador se puede escribir como:
C = κε 0 G = εG
6.15
Expresión en la cual G es un factor geométrico y tiene las dimensiones de longitud. Para un condensador de
placas paralelas G es A/d; para un condensador cilíndrico (Ejemplo 2) G es
2πL ln(a b) .
Se puede resumir la función de un dieléctrico entre las placas de un condensador en tres partes a saber:
1. Resuelve el problema mecánico de mantener dos grandes placas metálicas a distancia muy pequeña sin
contacto real alguno.
2. Puesto que su rigidez dieléctrica es mayor que la del aire, aumenta la diferencia máxima de potencial que
el condensador es capaz de resistir sin romperse.
3. La capacidad de un condensador de dimensiones dadas es varias veces mayor con un dieléctrico que
separe sus placas que si estuviera en el vacío.
Ejemplo 7. El espacio entre las placas de un condensador de placas planas paralelas de área está lleno con
dos bloques dieléctricos, uno con constante κ1 y espesor d1 y el otro con κ2 y espesor d2 como la figura 6.13.
La separación entre las placas es d.
Figura 6.13
En este ejemplo es importante hacer notar que hay solamente un condensador dentro del cual hay dos
medios dieléctricos que no se mezclan. NO HAY DOS CONDENSADORES EN SERIE.
Apuntes de física II
[email protected]
Cap. 6: Condensadores y dieléctricos 157
Apuntes de física II
Para calcular la capacitancia “equivalente” de este condensador se calcula primero el campo eléctrico en
cada medio usando la ley de Gauss, después la diferencia de potencial entre las placas y por último se aplica
la ecuación 6.1.
En la figura adjunta que aparece abajo a la derecha se han dibujado dos superficies gaussianas cilíndricas
con tapas de área S que abarcan el dieléctrico 1 y el dieléctrico 2 respectivamente. La separación d entre
las placas es muy pequeña comparada con A de modo que se pueden pasar por alto las irregularidades de
las líneas de fuerza en los extremos al calcular la capacitancia.
El flujo en la superficie que está dentro del conductor para cada superficie gaussiana es cero, porque el
campo eléctrico dentro de un conductor que tiene carga estática es cero. El flujo a través de las paredes de
los cilindros es cero porque las líneas de fuerza dentro del condensador son paralelas.
Así pues, solo quedan los flujos en cada cara
que está en los dieléctricos. Estos son:
ε 0κ 1 E1 S = σ L S y ε 0κ 2 E 2 S = σ L S
Entonces,
E1 =
σL
σ
y E2 = L
ε 0κ 1
ε 0κ 2
Que están de acuerdo con la ecuación 6.10.
La diferencia de potencial entre las placas es
v
v d1 + d 2 v
v
2 v
d2 v
V = − ∫ E ⋅ dl = − ∫ E 2 ⋅ dl − ∫
E1 ⋅ dl
1
Donde
v v
E1 y E 2
0
apuntan en direcciones opuestas a
d2
v
dl , o sea,
d2
d1 + d 2
0
d2
V = ∫ E 2 dl + ∫
V=
σL
ε0
E1 dl = E 2 d 2 + E1 d1
⎛ d1 d 2 ⎞
⎜⎜ + ⎟⎟
⎝ κ1 κ 2 ⎠
La capacitancia de ese condensador es
C=
σLA
qL
=
V
σ L ⎛ d1 d 2
⎜ +
ε 0 ⎜⎝ κ 1 κ 2
⎞
⎟⎟
⎠
=
ε 0 Aκ 1κ 2
d1κ 2 + d 2κ 1
Si d1=d2=d/2 la capacitancia se puede escribir como
C=
Si
2ε 0 Aκ 1κ 2 2ε 0 A
=
κ
d (κ 1 + κ 2 )
d
κ 1 = κ 2 = 1 , la capacitancia es la dada por la ecuación 6.2.
Ejemplo 8. Un voltímetro electroestático está formado por dos semicilindros coaxiales rígidamente unidos
que pueden girar alrededor de su eje, situado éste en la superficie de un líquido de constante dieléctrica κ
como se muestra en la figura 6.14. Los radios son a y b y la longitud de los cilindros es L. Hallar la
capacitancia de este sistema.
Apuntes de física II
[email protected]
Cap. 6: Condensadores y dieléctricos 158
Apuntes de física II
Figura 6.14
Usando el resultado del ejemplo 2 para un condensador cilíndrico se calculan los factores geométricos de
cada condensador y después, para hallar la capacitancia de cada uno de ellos se utiliza la ecuación 6.14.
Los factores geométricos son:
G1 =
αL
y
ln(b a )
G2 =
(π − α ) L
ln (b a )
Las capacitancias son:
C1 = ε 0 G1 =
C 2 = ε 0κG2 =
ε 0α L
ln(b a )
ε 0κ (π − α ) L
ln(b a)
=
ε (π − α ) L
ln(b a)
Los condensadores de la figura 6.14 están en una combinación en serie, se obtiene
C = C1 + C 2 =
ε0L
ln(b a)
(α + ε (π − α )) = ε 0 L (α (1 − ε ) + επ )
ln(b a )
Cuando ε=1 se tiene la capacitancia de un condensador semicilíndrico.
6.8 DESPLAZAMIENTO
v ELECTRICO.
Se define el desplazamiento D en cualquier punto
v
v
vector polarización P y del producto ε 0 E como:
de un dieléctrico polarizado como la suma vectorial del
v v
v
D = P + ε0E
Pero
6.16
v
v
v
v
v
P = ε 0 χ e E = ε 0 (κ − 1) E = (ε 0κ − ε 0 ) E = (ε − ε 0 ) E , de modo que en el dieléctrico
v
v
D = εE
En el vacío
v
P = 0,
6.17
v
v
D = ε0E
El concepto de desplazamiento eléctrico simplifica ciertas ecuaciones, y tiene propiedades útiles e
interesantes. La figura 6.15 muestra el condensador con dieléctrico.
Apuntes de física II
[email protected]
Cap. 6: Condensadores y dieléctricos 159
Apuntes de física II
Figura 6.15
v
La integral de superficie de E para la superficie gaussiana de la figura 6.15, formada por un cilindro una de
cuyas bases se encuentra en la placa metálica, y la otra, en el dieléctrico. Dentro de la placa metálica
v
E = 0.
En el interior del dieléctrico,
v
v
1
ˆ
E
⋅
n
dA
=
E
∫
∫ ⋅ nˆdA = (q L − q P )
ε0
S
La integral de superficie de
v
E
extendida a una superficie cerrada es igual a
6.18
1 ε 0 multiplicado por la carga
neta interior a la superficie, incluyendo tanto las cargas libres como las de polarización.
De la ecuación 6.18 se obtiene el campo eléctrico dentro del dieléctrico, que es:
E=
σ L qL
1
=
=
(q L − q P )
κ κA ε 0 A
Simplificando esta última ecuación se tiene:
1⎞
⎛
⎛ κ −1⎞
q P = ⎜1 − ⎟ q L = ⎜
⎟q L
⎝ κ⎠
⎝ κ ⎠
6.19
Esta expresión muestra que la carga superficial inducida qP es siempre menor en magnitud que la carga libre
κ
= 6 que al sustituirla en la ecuación 6.19
qL y es igual a cero cuando no hay dieléctrico. En el ejemplo 6,
da qP=(5/6)qL.
Al reemplazar la ecuación 6.19 en la ecuación 6.18 y haciendo operaciones, se obtiene:
v
qL
∫ E ⋅ nˆdA = ε κ
S
0
v
v
ε 0κ ∫ E ⋅ nˆdA = ∫ εE ⋅ nˆdA =q L
S
6.20
S
Esta relación es importante, aunque se ha derivado para un condensador de placas paralelas, es aplicable en
todos los casos.
Si en la ecuación 6.20 se reemplaza la ecuación 6.17 se obtiene:
v
D
∫ ⋅ nˆdA =q L
6.21
S
Que es la ley de Gauss para el vector desplazamiento eléctrico y es aplicable cuando hay dieléctricos.
Desarrollando la ecuación 6.21 para la gaussiana de la figura 6.15, se tiene que:
D =σL
Apuntes de física II
[email protected]
Cap. 6: Condensadores y dieléctricos 160
Apuntes de física II
En forma general la ecuación 6.16 y 6.21 son de validez general y puede extenderse a conductores de
cualquier forma.
En general para cualquier conductor, la densidad de carga se puede escribir como:
v
σ L = D ⋅ nˆ = D cos θ
6.22
Donde θ es el ángulo formado por el vector normal a la superficie y el vector desplazamiento eléctrico.
Ejemplo 9. Una esfera conductora de radio R, que tiene una carga qL, se introduce en un dieléctrico líquido
de constante dieléctrica κ como se muestra en la figura 6.16. ¿Cuál es la fuerza que ejerce sobre una carga
puntual q situada en el líquido a una distancia r del centro de la esfera?.
Figura 6.16
Se construye una superficie gaussiana de radio r, como en la figura. De la ecuación 6.21 y condiciones de
simetría se tiene:
v
∫ D ⋅ nˆdA = DA = D(4π r
2
S
D=
Pero
(1 4πε 0 )(q L
r2
1 qL
4π r 2
D
E=
y
ε
=
D
ε 0κ
) =q L
=
qL
4πε 0κ r 2
1
) es la intensidad del campo eléctrico E que produce en el vacío las cargas libres de
0
la esfera; o sea,
E=
E0
κ
La fuerza sobre la carga q es
F = qE =
1
κ
qE0 =
1 ⎛ 1 qq L ⎞
⎟,
⎜
κ ⎜⎝ 4πε 0 r 2 ⎟⎠
de modo que el efecto del dieléctrico es reducir la carga neta por el factor
v
D
Las propiedades del desplazamiento
previamente la carga de polarización qP.
1κ.
permite hallar el campo en la carga q, sin tener que calcular
6.9 ENERGIA ALMACENADA EN UN CONDENSADOR CARGADO.
El proceso de cargar un condensador consiste en el paso de carga desde la placa de menor a mayor
potencial y requiere, por tanto, consumo de energía. Se supone que el proceso de carga comienza con
Apuntes de física II
[email protected]
Cap. 6: Condensadores y dieléctricos 161
Apuntes de física II
ambas placas descargadas, y que después se saca repetidamente pequeñas cargas positivas de una de ellas
y se pasa a la otra. En un tiempo t ha pasado una carga q´(t) de una placa a la otra. La diferencia de
potencial V(t) entre las placas es q´(t)/C. Para incrementar la carga en una cantidad dq´, la cantidad de
trabajo necesaria para llevarla requiere un trabajo adicional dado por:
⎛ q´ ⎞
dW = Vdq = ⎜ ⎟dq´
⎝C ⎠
Si se continúa el proceso hasta cargar completamente el condensador con una carga q, el trabajo requerido
para ello es:
W =∫
q
0
q´
1 q2
dq´ =
C
2 C
6.23
Que queda como energía almacenada U en el condensador y es devuelta, de ordinario, en forma de chispa,
cuando el condensador se descarga.
Un condensador cargado es el equivalente eléctrico de un resorte estirado, cuya energía potencial elástica es
igual (1/2)Kx2. La carga q es análoga a la elongación x, y 1/C, a la constante elástica K.
También, se puede escribir la energía almacenada en el condensador cuando se reemplaza q=CV en la
ecuación 6.23 así:
U=
1
CV 2
2
6.24
Cuando entre las placas de un condensador se introduce un dieléctrico, la energía almacenada en él es
modificada por la presencia de este.
La energía U0 antes de introducir el dieléctrico es:
U0 =
1
C 0V02
2
6.25
Después de colocar el dieléctrico entre las placas del condensador, se tiene:
C = κC o
V=
y
V0
κ
y, por consiguiente,
2
1
1
1 ⎛1
⎛V ⎞
⎞ 1
U = CV 2 = κC 0 ⎜ 0 ⎟ = ⎜ C 0V02 ⎟ = C 0
κ ⎝2
2
2
⎠ κ
⎝κ ⎠
6.26
La energía después de introducir el dieléctrico es menor en un factor 1/κ .
La energía “Faltante” es fácil de comprender para el agente externo que introduce el dieléctrico dentro del
condensador. El condensador ejerce una fuerza sobre el dieléctrico y realiza trabajo sobre él, en la cantidad
de
W = U0 −U =
1⎞
1⎞
1
⎛
⎛
C 0V02 ⎜1 − ⎟ = U 0 ⎜1 − ⎟
2
⎝ κ⎠
⎝ κ⎠
6.27
Si el dieléctrico se introduce sin ningún esfuerzo y si no hay pérdidas por fricción, el dieléctrico oscila de un
lado al otro entre las placas del condensador.
Ejemplo 10. Un condensador de placas planas paralelas con un área A=L2 y una separación d. Una batería
carga las placas comunicándoles una diferencia de potencial V0. Entonces se desconecta la batería, y se
introduce un bloque dieléctrico de espesor d y constante dieléctrica κ como se muestra en la figura 6.17.
Apuntes de física II
[email protected]
Cap. 6: Condensadores y dieléctricos 162
Apuntes de física II
Hallar, como función de x, a) la capacitancia equivalente del sistema, b) la energía del sistema, c) la fuerza
ejercida sobre el bloque y d) la fuerza promedio necesaria para introducir todo el bloque dieléctrico.
Figura 6.17
a) Para la situación de la figura 6.17 hay dos condensadores en paralelos con una capacidad equivalente
dada por:
C ( x) = C L − x + C x =
C ( x) =
ε0
d
(L( L − x) + κLx ) = ε 0 L
ε0A ⎛ L − x
⎜
d ⎝ L
⎛ L − x κx ⎞
+ ⎟
⎜
d ⎝ L
L⎠
2
+
κx ⎞
⎛ L − x κx ⎞
+ ⎟
⎟ = C0 ⎜
L⎠
L⎠
⎝ L
⎛ (κ − 1) x ⎞
C ( x ) = C 0 ⎜1 +
⎟
L ⎠
⎝
Se observa que cuando x=0, C(0)=C0 y cuando x=L, C(L)=κC0.
b) La energía potencial para la configuración mostrada, en términos de x es:
U ( x) =
C
1 q2
1 C0 q 2
=
= U0 0
2 C ( x) 2 C o C ( x)
C ( x)
⎛ (κ − 1) x ⎞
U ( x ) = U 0 ⎜1 +
⎟
L ⎠
⎝
−1
c) En la figura 6.17 se muestra como se producen las fuerzas sobre la placa dieléctrica en función de la
atracción entre la carga libre de las placas y las cargas superficiales inducidas que aparecen en el
dieléctrico cuando este se introduce en el condensador. Para que el dieléctrico penetre sin aceleración hay
que sostenerlo con una fuerza como se muestra en la figura. Esto significa que se tiene que hacer trabajo
negativo sobre el dieléctrico, o, considerando a la inversa, que el sistema condensador + dieléctrico tiene
que hacer trabajo positivo. Este trabajo para introducir el dieléctrico una cantidad x en el condensador es el
dado por U(x). Por lo tanto la fuerza para cualquier posición a lo largo de x es:
Fx = −
−1
−1
dU ( x)
d ⎡ ⎛ (k − 1) ⎞ ⎤
d ⎛ (κ − 1) ⎞
= − ⎢U 0 ⎜1 +
x ⎟ ⎥ = −U 0 ⎜1 +
⎟
dx
dx ⎢⎣ ⎝
L
dx ⎝
L ⎠
⎠ ⎥⎦
(κ − 1) ⎛ (κ − 1) x ⎞
Fx = U 0
⎟
⎜1 +
L ⎝
L ⎠
−2
=
U 0 (κ − 1) L
(L + (κ − 1) x )2
d) La fuerza promedio para introducir completamente el condensador entre las placas se puede hallar de dos
maneras, a saber:
Apuntes de física II
[email protected]
Cap. 6: Condensadores y dieléctricos 163
Apuntes de física II
1) Directamente de la ecuación 6.27 como:
1⎞
⎛
W = F prom L = U 0 ⎜1 − ⎟
⎝ κ⎠
Entonces la fuerza promedio es:
Fprom =
W U0
=
L
L
⎛ 1 ⎞ U 0 (κ − 1)
⎜1 − ⎟ =
κL
⎝ κ⎠
2) Se halla usando el resultado obtenido en c) y de la definición de
F porm =
Haciendo
F prom , como:
L
1 L
1 L U 0 (k − 1) L
(κ − 1)
F
dx
dx
U
dx
=
=
0
x
2
∫
∫
∫
0
0
0
L
L (L + (κ − 1) x )
( L + (κ − 1) x) 2
u = L + (κ − 1) x
y
du = (κ − 1) , se tiene que
F prom = U 0 ∫
κL
L
κL
du
⎛ 1 1⎞
= U 0 ∫ u − 2 du = −U 0 ⎜
− ⎟
2
L
u
⎝ κL L ⎠
F prom =
U0
L
⎛ 1 ⎞ U 0 (κ − 1)
⎜1 − ⎟ =
κL
⎝ κ⎠
Como era de esperarse.
Hasta ahora se ha asociado la energía de un condensador con la energía potencial de sus cargas, otro punto
de vista es atribuir esta energía al campo eléctrico que existe entre las placas. Así, por ejemplo, cuando se
aumenta q o V en las ecuaciones 6.23 y 6.24, aumenta también el campo eléctrico E; cuando q y V valen
cero, también E vale cero.
En general la capacitancia de un condensador de placas paralelas, con dieléctrico como en la figura 6.15, es
C=
ε 0κA
d
=
εA
d
El potencial eléctrico entre las placas del condensado, es
V = Ed
La energía almacenada en este condensador esta dada por
U=
1
1 ε 0κA
1
( Ed ) 2 = ε 0κE 2 ( Ad )
CV 2 =
2
2 d
2
U=
1 2
εE ( Ad )
2
6.28
Donde Ad es el volumen del espacio comprendido entre las placas.
Así pues, la densidad de energía u, que es la energía por unidad de volumen, si no se han tomado en cuenta
las irregularidades en los bordes, es uniforme en el volumen y está dada por
Apuntes de física II
[email protected]
Cap. 6: Condensadores y dieléctricos 164
Apuntes de física II
u=
(1 2)εE 2 ( Ad )
U
=
volumen
Ad
u=
1 2 1
εE = ε 0κE 2
2
2
6.29
Esta ecuación, aunque se derivó para un condensador de placas paralelas se puede aplicar de forma general
v
para todos los casos en donde exista un campo eléctrico E .
La ecuación 6.29 se puede expresar en términos del vector desplazamiento así:
u=
1 r v 1 v v 1 D2
εE ⋅ E = D ⋅ E =
2
2
2 ε
Ejemplo 11. Un condensador esférico está conformado por una esfera concéntrica a un cascaron esférico de
radios a y b respectivamente como se muestra en la figura 6.18, con
b⟩ a
y
κ =1.
a) Hallar la energía
electrostática almacenada en el condensador. b) La capacitancia de ese condensador. c) ¿Cuál es el radio
R0 de una superficie esférica dentro del condensador tal que quede la mitad de la energía almacenada?.
a) A cualquier distancia radial
a⟨r ⟨b
Figura 6.18
del centro de la esfera y para la superficie gaussiana mostrada por
líneas interrumpidas en la figura el campo eléctrico
E0 =
v
E0
es:
1
q
4πε 0 r 2
La densidad de energía a cualquier distancia radial r se obtiene de la ecuación 6.29, con
u=
k = 1 , o sea,
1
1
q2
ε 0 E02 =
2
32π 2 ε 0 r 4
La energía dU que hay en un cascaron esférico entre los radios r y r+dr es:
dU = (4π r 2 dr )u =
Apuntes de física II
q 2 dr
8πε 0 r 2
[email protected]
Cap. 6: Condensadores y dieléctricos 165
Apuntes de física II
La energía total U almacenada en el condensador es:
U=
q2
8πε 0
dr
q2 ⎛ 1 1 ⎞
=
−
∫a r 2 8πε 0 ⎜⎝ b − a ⎟⎠
b
U=
q2
8πε 0
⎛b−a⎞
⎟
⎜
⎝ ab ⎠
b) La capacitancia de este condensador esférico se halla igualando la ecuación 6.23 con la energía
encontrada en el numeral anterior así:
U=
q2 ⎛ b − a ⎞
1 q2
=
⎟
⎜
2 C 8πε 0 ⎝ ab ⎠
1
1 ⎛b−a⎞
=
⎜
⎟
C 4πε 0 ⎝ ab ⎠
⎛b−a⎞
C = 4πε 0 ⎜
⎟
⎝ ab ⎠
c) ½ U de la energía obtenida en a) se iguala a la energía entre a y R0 como:
1
q2
U=
2
16πε 0
q2
⎛b−a⎞
=
⎟
⎜
⎝ ab ⎠ 8πε 0
∫
R0
a
dr
r2
1 ⎛ b − a ⎞ ⎛ R0 − a ⎞
⎟ ; R0 (b − a ) = 2b( R0 − a)
⎟=⎜
⎜
2 ⎝ ab ⎠ ⎜⎝ aR0 ⎟⎠
De donde se obtiene, después de hacer algunas operaciones,
R0 =
Apuntes de física II
2ba
b+a
[email protected]