teoría de vectores
Anuncio

Geometría: Vectores en el espacio Matemáticas 2 Geometría: Vectores en el espacio 1. Concepto de vector Sabemos que el conjunto de matrices Mmxn con las operaciones suma y producto por números reales es un espacio vectorial sobre R. Por tanto, si consideramos el subconjunto de las matrices M1xn es también un espacio vectorial. 2. Conjunto R3 Si creamos el producto cartesiano de RxRxR, que designaremos por R3, como: R3 RxRxR todas las ternas ordenadas formadas por números reales 1 x, y, z t.q. x R, y R, z R ...., 0,0,1, 3,2,7 , ,5,8 , 2 2 ,1, 5 , ... x = primera coordenada, y = segunda coordenada, z = tercera coordenada Hay que tener en cuenta que son ternas ordenadas, la (3,4,1) es distinta de la (4,3,1). Todo el mundo debe saber asociar una terna con un punto en el espacio real. Es evidente que el conjunto así definido coincide con el subconjunto de matrices M1x3 que por tanto, con las correspondientes operaciones suma y producto por un escalar, le dotan de estructura de espacio vectorial. De esta identidad con M1x3 podemos deducir que: “Para que dos ternas de números sean iguales deben de ser iguales sus primeras, sus segundas y sus terceras coordenadas” Ejemplo 1: Calcular “a”, “b” y “c” para que se verifique la siguiente igualdad: (2a,b,6)=(-1,1,3c) Veamos como quedan definidas las operaciones en R3. - 1/22 - A.G.Onandía Geometría: Vectores en el espacio Matemáticas 2 3. Operaciones básicas en R3 Vamos a definir dos operaciones en R3. 3.1 Suma en R3 : Definición: x, y, z R 3 , x' , y ' , z ' R3 (x,y,z)+(x’,y’,z’)=(x+x’,y+y’,z+z’) Propiedades: 1.- Es una operación interna: al sumar dos ternas reales obtenemos otra terna real. 2.- Asociativa: x, y, z R 3 , x' , y ' , z ' R3 , x' ' , y ' ' , z ' ' R3 (x,y,z)+[(x’,y’,z’)+(x’’,y’’,z’’)]=[(x,y,z)+(x’,y’,z’)]+(x’’,y’’,z’’) 3.- Conmutativa: x, y, z R 3 , x' , y ' , z ' R 3 (x,y,z)+(x’,y’,z’)=(x’,y’,z’)+(x,y,z) 4.- Existencia de elemento neutro. x, y, z R 3 a, b, c R3 tq (a,b,c)+(x,y,z)=(x,y,z) a x x a 0 b y b b 0 (a,b,c)=(0,0,0) c y c c 0 5.- Existencia de elemento simétrico . El elemento simétrico para la suma se denomina elemento opuesto. x, y, z R 3 a' , b' , c' R3 tq (x,y,z)+(a’,b’,c’)=(0,0,0) x a' 0 a' x y b' 0 b' y (a’,b’,c’)=(-x,-y,-z) z c' 0 c' z Recordar que: todo conjunto con una operación interna que verifica estas propiedades se dice que es un grupo conmutativo. - 2/22 - A.G.Onandía Geometría: Vectores en el espacio Matemáticas 2 3.2 Producto de un número real por una terna de R3 : Definición: x, y, z R 3 , R (x,y,z)=(x, y, z) Propiedades: 1.- Es una operación (o ley) externa, ya que a cada número real “” y a cada terna (x,y,z) de R3 le asociamos una nueva terna de R3 (x,y,z) 2.- Distributiva de la ley externa respecto de la interna . Sea R, (x,y,z)R3, (x’,y’,z’)R3 [(x,y,z)+(x’,y’,z’)]=(x,y,z)+(x’,y’,z’) 3.- Distributiva de la ley externa respecto a la suma de números reales: Sea R, µR, (x,y,z)R3 (+µ)(x,y,z)=(x,y,z)+µ(x,y,z) 4.- Existencia de elemento neutro x x x, y, z R R t.q. x, y, z x, y, z y y 1 z z 3 5.- Asociativa mixta , R , x, y, z R 3 [µ(x,y,z)]=µ(x,y,z) (µx,µy,µz)=(µx,µy,µz)=µ(x,y,z) Recordar que: Todo conjunto que tiene dos operaciones, una interna y otra externa, que además para la operación interna es un grupo conmutativo y que para la operación externa verifica las 5 propiedades anteriores, se dice que tiene una estructura de ESPACIO VECTORIAL. Luego (R3,+,.) es un espacio vectorial, por ello a los elementos de R3 les llamamos VECTORES NUMÉRICOS y los denotamos por u , v , … p. ej. u 3,5,7 Ejemplo 2: a) -7(5,-1,3)+3(2,5,-1)= b) [2(1,-2,-4)+5(-2,3,0)]-(1/2)(4,6,7)+6(-1,8,3)= - 3/22 - A.G.Onandía Geometría: Vectores en el espacio Matemáticas 2 4. Vectores libres en el espacio. 4.1 Introducción. Vectores fijos. Hay magnitudes que no quedan bien definidas únicamente con un número p.ej. velocidad, fuerza, … de ellas se necesita conocer su dirección y sentido. A estas magnitudes se les denominan vectoriales y se representan por lo que denominamos vectores fijos. Definición: Un vector fijo es un segmento orientado que tiene su origen en A y extremo en B y se denota por AB . Al conjunto de todos los vectores fijos del espacio se le denota por F3. B A El punto A del vector fijo AB se denomina origen y B extremo Para determinar un vector fijo hemos de conocer su módulo, dirección, sentido y origen: MÓDULO de un vector AB es la longitud del segmento que une los puntos A y B. Se representa por AB . DIRECCIÓN de un vector AB es la recta que pasa por A y B y todas sus paralelas. Dos vectores no nulos tienen la misma dirección si se encuentran en rectas paralelas SENTIDO de un vector AB es el recorrido de la recta cuando vamos de A a B. Cada dirección tiene dos sentidos. ORIGEN de un vector AB es el punto A Un caso particular de vector es el vector nulo, que tiene su origen y extremo en el mismo punto: AA, BB, .... - 4/22 - A.G.Onandía Geometría: Vectores en el espacio 4.1.1 Matemáticas 2 Componentes cartesianas de un vector fijo Si consideramos en el espacio el sistema cartesiano de coordenadas cualquier punto A queda determinado por sus tres coordenadas cartesianas. Definición: Sean A(x, y,z) y B(x’, y’,z’) dos puntos del espacio las componentes del vector AB son B A x' x, y ' y, z ' z se representa por AB x' x, y' y, z' z y gráficamente son sus proyecciones sobre el eje OX, el eje OY y el eje OZ, respectivamente. Ejemplo 3: Dados los puntos A(2,5,7) y B(3,1,9), calcular: a) Las componentes del vector fijo AB b) Un vector fijo con las mismas componentes que AB cuyo origen esté en C(-3,-1,7). 4.1.2 Equipolencia de vectores fijos Entre los vectores fijos vamos a establecer una relación que llamaremos relación de equipolencia. Definición: Dos vectores fijos AB y CD son equipolentes si tienen las mismas componentes i.e. AB a, b, c y CD (d , e, f ) AB CD a d y b e y c f Hay otras tres formas semejantes de definirlas: 1.- AB CD si cumplen una de las siguientes condiciones: B Si son dos vectores no nulos y no contenidos en la misma recta D ABDC tiene que formar un paralelogramo (Regla del paralelogramo) A C Si los dos vectores son no nulos y están contenidos en la E F misma recta, debe de existir un tercer vector EF de modo que A ABFE y CDFE son paralelogramos. B C D B AB y CD son nulos 2.- AB CD si los puntos medios de AD y BC coinciden D A C 3.- AB CD si tienen la misma dirección, módulo y sentido. Ésta es intuitivamente la más fácil de manejar. - 5/22 - A.G.Onandía Geometría: Vectores en el espacio Matemáticas 2 Ejemplo 4: Determinar que vectores son equipolentes en el hexágono y ortoedro adjuntos A E F F E B D H G C C A B D Ejemplo 5: Las componentes del vector fijo AB son (3,2,5), calcular el punto A si B(1,-1,8) Ejemplo 6: Dados los puntos A(1,-3,5) y B(-2,-1,6), calcular: a) Las componentes del vector fijo AB b) Un vector fijo equipolente a AB cuyo origen sea el punto C(4,-1,0) c) Un vector fijo equipolente a AB cuyo extremo sea el punto F(1,3,7) Ejemplo 7: Dados los puntos A(5,2,-1) y B(1,-2,3) calcular: a) Las componentes del vector fijo AB b) Un vector fijo equipolente a AB cuyo origen sea el punto C(-1,0,-1) c) Idem. con extremo en el punto F(2,2,2) 4.2 Vectores libres sus equipolentes: AB XY tq XY AB Definición : Llamaremos vector libre AB al conjunto constituido por un vector fijo AB y todos Un vector libre contiene todos los vectores de igual módulo, dirección y sentido. Los vectores libres se denotan con letras minúsculas u , v , w, ... Al conjunto de todos los vectores libres del espacio le denotamos por V3. Se llama dirección, módulo y sentido de un vector libre no nulo a la dirección, módulo y sentido de cualquiera de sus representantes. Se entiende por representante cualquier vector fijo contenido en el vector libre. Una propiedad de los vectores libres llamada propiedad fundamental es: Teorema: “Cualquier vector libre u tiene un único representante con origen en un punto O arbitrario del espacio” - 6/22 - A.G.Onandía Geometría: Vectores en el espacio Matemáticas 2 Demostración: Sea u un vector libre cuyo representante es AB i.e. u AB 1.- si O no pertenece a la recta que pasa por A y B, construimos el B paralelogramo ABPO como intersección de una recta paralela a la que pasa P A por A y B pasando por el punto O, de la recta que pasa por A y O y por la O recta por la recta paralela a la que pasa por A y O pasando por B, entonces: AB u y AB OP OP u u OP i.e. OP es un representante de u . La unicidad viene dada de por la unicidad de la existencia del punto P, como intersección de dos rectas no paralelas. 2.- Si el punto O pertenece a la recta que pasa por A y B. Elegimos un punto arbitrario C que no está en la recta que pasa por A y B. Como C no está en la mencionada recta, por el apartado 1, existe un único representante que pase por C. Ahora nos quedamos con este representante y nos fijamos que el punto O no está en la recta que contiene a este representante, por el apartado 1, existe un único representante que pasa por O. A P O D C u AB u CD AB CD B u CD u OP OP CD La importancia de este teorema lo veremos cuando realicemos las operaciones con vectores libres. Ejemplo 8: Dados los puntos A(3,-4,5) y B(2,0,-4), calcular: a) las componentes del vector libre u uno de cuyos representantes es AB b) el origen y el extremo de otro vector fijo que también sea representante de u 4.2.1 Vector posición de un punto Definición: Dado un punto cualquiera P R 3 , llamamos vector de posición del punto P, al vector que tiene por origen el origen de coordenadas y por extremo el punto P, es decir al vector OP , que lo denotaremos por p . - 7/22 - A.G.Onandía Geometría: Vectores en el espacio Matemáticas 2 Se verifica que las componentes del vector p coinciden con las coordenadas del punto P. Sea P(x,y,z) p OP x 0, y 0, z 0 x, y, z Luego aplicando la propiedad fundamental de los vectores libres, cualquier vector libre AB , tiene un representante en el origen de coordenadas OQ q , y las componentes de este vector coinciden con las coordenadas cartesianas de su extremo Q. Así, a cada vector libre le puedo asociar un punto y viceversa. Ahora, teniendo en cuenta que tener un vector libre es equivalente a tener un punto y esto es exactamente igual a tener un vector numérico, podemos deducir que los vectores libres se pueden manejar igual que los vectores numéricos y por tanto tienen sus mismas propiedades. Esto es interesante a la hora de plantear y resolver ejercicios. 4.2.2 Operaciones con vectores libres Definición: Dos vectores libres son iguales cuando sus representantes son equipolentes i.e cuando tienen las mismas componentes u v AB CD siendo u AB y v CD Es una definición similar a la que hemos dado para igualdad de vectores numéricos. 4.2.2.1 Adición Definición: Para sumar dos vectores u y v se representa uno de ellos u , y con u origen en el extremo de u , se representa el otro vector v . El vector suma de u v ambos, es el que tiene el origen de u y el extremo de v . También se pude sumar aplicando la ley del paralelogramo: “Se representan los vectores u y v con el mismo origen. El vector suma es la diagonal del paralelogramo formado con u y v .” u v u v v Propiedades: 1.- Asociativa: u v w u v w 2.- Conmutativa: u + v = v + u 3.- Existencia de elemento neutro: o + u = u con o AA - 8/22 - A.G.Onandía Geometría: Vectores en el espacio Matemáticas 2 4.- Existencia de elemento opuesto: u +(- u )= o con u BA El opuesto de un vector libre es otro vector libre de igual módulo, dirección y sentido contrario, que nos permite definir la diferencia como u v u v El conjunto de todos los vectores libres del espacio lo denotaremos por V3. Así (V3,+) es un grupo conmutativo. Ejemplo 9: Dados los vectores libres u (2,-1,9) y v (-3,4,3) calcular s = u + v Ejemplo 10: Si AB es un representante del vector libre u y CD de v siendo A(0,1,8), B(3,-2,-1), C(1,0,1) y D(4,7,-1), calcular: a) s = u + v b) Un representante de s con origen en el punto E(2,1,1) 4.2.2.2 Producto de un número real por un vector Definición: Al multiplicar un vector u por un número real k, obtenemos un nuevo vector libre ku que tiene: - igual módulo al del vector u por el valor absoluto del número k | ku |=|k|| u | - igual dirección que la del vector u - el mismo sentido que u si k es positivo ó contrario si k es negativo. - si k=0 le hacemos corresponder el vector nulo 2u Ejemplo 11: 2 u y -3 u u u 3u Propiedades: 1.- Distributiva del producto respecto de la suma k u v ku kv 2.- Distributiva del producto respecto a la suma de números reales u k t ku tu 3.- Asociativa mixta k tu kt u 4.- Elemento neutro para el producto 1. u = u - 9/22 - A.G.Onandía Geometría: Vectores en el espacio Matemáticas 2 Luego el conjunto de los vectores libres con la suma y el producto por un escalar es un espacio vectorial que se denota por (V3,+,.). 4.2.3 Combinación lineal de vectores en V3 Definición: Dado un vector en el espacio v V 3 , se dice que es combinación lineal de un conjunto de vectores del espacio u1 , u2 , ..., un , si es posible encontrar unos números reales 1, 2,…,n, no todos nulos, tales que v 1u1 2 u2 ... nun Se dice que un conjunto de vectores son linealmente dependientes o que forman un sistema ligado, si uno cualquiera de ellos puede expresarse como combinación lineal de los demás. En caso contrario diremos que son linealmente independientes o forman un sistema libre. Esta definición de dependencia lineal es poco operativa la que se utiliza: Definición: Se dice que un conjunto de vectores u1, u2 , ...,un V 3 son linealmente independientes si la única combinación lineal de ellos es la trivial es decir: si 1u1 2 u2 ... nun 0 entonces i 0 i 1,..., n Gráficamente tres vectores (no nulos) son L.I. si tienen distinta dirección i.e .no son coplanarios Nosotros utilizaremos otra herramienta que ya conocemos y que nos da información sobre la independencia lineal de vectores como es el rango de las matrices que construimos con los vectores. Ejemplo 12: Comprobar si los vectores i (1,0,0); j (0,1,0) y k 0,0,1 son L.I. Aplicando directamente la definición operativa: 1 1,0,0 2 0,1,0 3 0,01 0,0,0 1 2 3 0 1 0 0 Esto también se puede comprobar calculando el rango de la matriz M 0 1 0 hacemos su 0 0 1 determinante |M|=1≠0 luego RgM=3 i.e los vectores filas (columnas) son L.I. Ejemplo 13: Indicar cuantos vectores L.I. del siguiente conjunto de vectores: 1,2,0, 1,0,2, 2,6,2, 4,12,4 . - 10/22 - A.G.Onandía Geometría: Vectores en el espacio Matemáticas 2 1 2 1 0 Se trata de hallar el rango de M 2 6 4 12 0 2 fijarse que el rango máximo de M es 3 al ser 2 4 vectores de V3 por tanto el número máximo de vectores de V3 L.I. es 3. Orlando el menor de orden 2: 1 2 1 0 1 2 0 1 0 orlando se tiene 1 0 2 1 2 6 2 4 2 0 0 2 0 RgM 2 dos vectores L.I. 12 4 Definición: Un conjunto de vectores constituye un sistema generador si cualquier vector del espacio se puede expresar como C.L. de ellos i.e. v1, v2 , ..., vn V 3 sistema generador wV 3 1, ..., n R t.q. w 1v1 2v2 ... nvn Definición: Una base de un espacio vectorial es un sistema generador formado por vectores L.I. Una base del plano V3 está formada por tres vectores de V3 L.I. Teniendo en cuenta lo que hemos visto antes, podemos decir que gráficamente tres vectores no nulos y no coplanarios forman una base de V3. En el espacio, al igual que ocurría en el plano, existen infinitas bases, es decir, infinitos conjuntos de tres vectores L.I. en función de los cuales pueden expresarse todos los vectores del espacio. De todas las bases que podemos elegir de V3 la más sencilla es la formada por los vectores i ; j ; k (1,0,0); (0,1,0), 0,0,1 por ello se la denomina BASE CANÓNICA de V3. Estos tres vectores tienen la propiedad de ser perpendiculares y tener módulo 1. Si u1 , u2 , u3 es una base de V3 llamamos componentes del vector w a los 1, 2 , 3 tal que w 1u1 2u2 3u3 i.e. w1, 2 , 3 en . Ejemplo 14: Demostrar si los vectores u1 0,0,1; u2 2,1, 0, u3 (3,0,1) forman una base de V3. Hallar las componentes del vector (-11,-1,1) en dicha base. Sol: (2,1,3) Ejemplo 15: Hallar la condición que deben verificar los valores a y b para que el vector (a,-2,b) sea linealmente dependiente con los vectores. (1,2,4) y (-1,0,3). Sol: 3a+b+7=0 - 11/22 - A.G.Onandía Geometría: Vectores en el espacio Matemáticas 2 5. Aplicaciones geométricas de los vectores 5.1 Coordenadas del punto medio de un segmento Sea el segmento AB con A(x1, y1,z1) y B(x2, y2,z2) y M(xm, ym,zm) el punto medio. 1 1 1 m a AM a AB a (b a ) (a b) 2 2 2 A a M m Pasando esta ecuación vectorial a componentes tenemos: B b xm , ym , zm 1 x1 , y1 , z1 x2 , y2 , z2 1 x1 x2 , y1 y2 , z1 z2 2 x1 x2 xm 2 y1 y2 Ecuación analítica ym 2 z z zm 1 2 2 O 2 Segunda demostración: AM MB xm x1 , ym y1 , zm z1 x2 xm , y2 ym , z2 zm igualando las componentes obtenemos x1 x2 2 y1 y2 ym y1 y2 ym 2 ym y1 y2 ym 2 z1 z2 zm z1 z2 zm 2 zm z1 z2 zm 2 xm x1 x2 xm 2 xm x1 x2 xm Como generalización podemos hallar los puntos que dividen un segmento en un determinado número de partes. Dividir el segmento AB en n+1 partes iguales. Tenemos que hallar los n números ( k1, k2, Ak1 , kn) que lo dividen en n+1 partes. Para ellos partiremos de que: AB AB AB , Ak 2 2 , Ak 3 3 , n 1 n 1 n 1 - 12/22 - , Ak n n AB n 1 A.G.Onandía Geometría: Vectores en el espacio Matemáticas 2 Ejemplo 16: Hallar los puntos P y Q que dividen ala segmento AB en tres partes iguales con A(3,2,7) y B(5,10,-2). A P q p a 1 11 14 p a AB , ,4 3 3 3 Q B 2 13 22 q a AB , ,1 3 3 3 b O 5.2 Puntos alineados Tres o más puntos A1, A2, …,An están alineados (i.e. son colineales) si están en la misma recta. Vectorialmente esto quiere decir que A1 A2 , A1 A3 , … , A1 An tienen la misma dirección, por lo que se deben de ser proporcionales, es decir existen n-2 escalares k1, … ,kn-2 tal que A1 A2 =k1 A1 A3 = … =kn-2 A1 An . Utilizando rangos Rg( A1 A2 , A1 A3 , … , A1 An )=1 Ejemplo 17: Comprobar si están alineados los siguientes puntos: a) A(2,3,4), B(1,3,-2), C(3,3,10) Si b) P(2,4,4), Q(-3,2,1), R(7,4,9) No Ejemplo 18: Hallar “p” sabiendo que los puntos A(2,5,-1), B(4,3,3) y C(0,p,-5) están alineados. 2 Sol p=3 Rg AB, AC Rg 2 2 4 2 1 p 5 4 2 2 0 2 p 14 0 p 3 . p5 5.3 Puntos coplanarios Cuatro o más puntos A1, A2, …,An son coplanarios si están en el mismo plano. Esto quiere decir que entre los vectores A1 A2 , A1 A3 , … , A1 An hay a lo sumo dos linealmente independientes y por tanto Rg( A1 A2 , A1 A3 , … , A1 An )≤2 Ejemplo 19: Calcular el valor de “a” para que los cuatro puntos estén en el mismo plano (a,0,1), (0,1,2), (1,2,3), (7,2,1). a Sol: 1 a 1 1 2 2 0 a 1 7a 2 0 - 13/22 - A.G.Onandía Geometría: Vectores en el espacio Matemáticas 2 5.4 Baricentro de un triángulo Se trata de hallar las coordenadas del baricentro de un triángulo conociendo las de sus vértices. Recordemos que el baricentro de un triángulo es el punto donde B se cruzan las medianas. Y tiene la propiedad de que divide a P cualquiera de las medianas en dos segmentos tales que la longitud de A uno de ellos es el doble del otro. G M AG BG CG 2 GM GN GP N podemos escribir AG 2 GM C como M es el punto medio de BC x x y yc z b z c A(xa, ya, za) , B(xb, yb, zb) , C(xc, yc, zc) , G(xg, yg, zg) M b c , b , y por 2 2 2 tanto y ya z z x xc AG 2 GM xg xa , y g ya , z g za 2 b xg , b yg , b a z g 2 2 2 xa xb xc 3 ya yb yc y g ya yb yc 2 y g y g 3 z zb z c z g z a zb z c 2 z g z g a 3 xg xa xb xc 2 xg xg Ejercicios. - 14/22 - A.G.Onandía Geometría: Vectores en el espacio Matemáticas 2 6. Producto escalar Definición: El producto escalar de dos vectores u y v es un número real que se obtiene del modo siguiente: u v cosu , v si u y v no nulos u .v = si u ó v nulo 0 De esta definición se desprende que si los vectores son perpendiculares (ortogonales) el u v u.v 0 producto escalar es 0, es decir Ejemplo 19: Calcular (2 u -3 v )(3 u + v ) sabiendo que u . v =2,5, | u |=1, | v |=2. Sol. -47/2 6.1 Interpretación geométrica v v proyv u u u proyu v proyu v v cos proyv u u cos =( u , v )=menor de los ángulos formados por ambos vectores proyu v =proyección del vector v sobre el vector u. proyv u =proyección del vector u sobre el vector v. Tenemos que u . v = u v cos = u proyu v = v proyv u “El producto escalar de dos vectores es igual al módulo de uno de ellos por la proyección del otro sobre el primero” Ejemplo 20: Si | u |=6 y u . v =-8; hallar razonadamente 18 proyu v 6.2 Propiedades del producto escalar 1.- u . u ≥0 2 Demostración: u .u u u cos 0 u 0 Corolario: Definición de módulo de un vector u u.u 2.- Conmutativa: u . v = v . u Demostración: u.v u v cos(u , v ) v u cos(v , u ) v .u 3.- Homogénea o asociativa del producto de un número real por el producto escalar de dos vectores: k R , u , v V 3 k u.v ku .v u.kv - 15/22 - A.G.Onandía Geometría: Vectores en el espacio Matemáticas 2 Demostración: v Si k=0 trivial Si k>0 (k u ). v =|k u |.| v |cos(k u , v )=|k|| u || v |cos( u , v )= u =k| u || v |cos( u , v )=k( u . v ) ku Si k<0 (k u ). v =|k u |.| v |cos(k u , v )=|k|| u || v |cos= v =-k| u || v |cos(-)=-k| u || v |(-cos(-))= ku u =k| u || v | cos=k( u . v ) 4.- Distributiva del producto escalar con respecto a la suma : u .( v + w )= u . v + u . w Ejemplo 21: Comprobar estas propiedades con los vectores u (2,6,1), v (3,1,1) y w(8,1,5) y k=-2 6.3 Expresión analítica del producto escalar en la base canónica Sea e1 , e2 , e3 una base cualquiera del espacio y sean u y v dos vectores que podrán u u1e1 u2e2 u3e3 expresarse como C.L. de la base : el producto escalar será v v1e1 v2e2 v3e3 u .v u1e1 u2e2 u3e3 . v1e1 v2e2 v3e3 u1.v1.e1.e1 ) u1.v2 .(e1.e2 ) u1.v3 .(e1.e3 ) u2 .v1.(e2 .e1 ) u2 .v2 .(e2 .e2 ) u2 .v3 .(e2 .e3 ) u3 .v1.(e3 .e1 ) u3 .v2 .(e3 .e2 ) u3 .v3 .(e3 .e3 ) e1.e1 e1.e2 matricialmente lo podemos expresar: u .v u1 u2 u3 e2 .e1 e2 .e2 e .e e .e 3 1 3 2 e1.e3 v1 e2 .e3 v2 (expresión 1) e3 .e3 v3 Observación: la segunda matriz es simétrica, pues el p.e. es conmutativo. Esta expresión se puede simplificar mucho si elegimos adecuadamente la base. Definición: Un vector u se dice que es unitario (normado) si u 1 . Normalizar un vector es obtener otro vector a partir de él, que tenga la misma dirección y sentido y de módulo 1, para ello lo único que hay que hacer es dividirlo por su módulo u 3 u V v u - 16/22 - A.G.Onandía Geometría: Vectores en el espacio Matemáticas 2 Demostración: u u u 3 u V v v 1 , luego ya tenemos la unicidad del módulo. La misma u u u dirección y sentido viene dado de que | u | es un número positivo. Definición: Tres vectores u , v , w V3 se llaman ortogonales si lo son entre sí es decir u v , u w , v w y si además son de módulo 1 (| u |=| v |= w =1) son ortonormales. Definición: Una base cuyos vectores son perpendiculares y de módulo 1 recibe el nombre de base ortonormal. Expresión analítica del producto escalar en la base canónica Un ejemplo de base ortonormal es la base canónica i ; j ; k (1,0,0); (0,1,0), 0,0,1. Utilizando esta base la 2ª matriz de la expresión 1 se convierte en la matriz identidad, pues i j i . j j .i 0 i k i .k k .i 0 y i j k 1 i .i j . j k .k 1 . j k j .k k . j 0 El producto escalar en una base ortonormal resulta: u.v u1.v1 u2 .v2 u3 .v3 expresión analítica del producto escalar Mientras no se indique lo contrario emplearemos bases ortonormales 2 2 2 Como consecuencia de la expresión analítica del p.e. tenemos que u u.u u1 u2 u3 6.4 Ángulo formado por dos vectores De la propia definición u .v u . v =| u |.| v |cos( u , v ) cos( u , v )= uv Consecuencias: - Dos vectores paralelos de igual sentido u . v =| u |.| v | - Dos vectores paralelos de distinto sentido u . v =-| u |.| v | Si tomamos una base ortonormal cosu , v u1.v1 u2 .v2 u3 .v3 u12 u22 u32 v12 v22 v32 - 17/22 - A.G.Onandía Geometría: Vectores en el espacio Matemáticas 2 6.5 Cosenos directores Son los cosenos de los ángulos que forman el vector u con cada uno de los vectores de la base canónica u. i u1 u 2 u 3 1 0 0 u1 cos cos(u , i ) u .1 u ui u1 u cos u. j u1 u 2 u 3 0 1 0 u 2 cos cos(u, j) u .1 u u j u 2 u cos u.k u1 u 2 u 3 0 0 1 u 3 cos cos(u , k ) u .1 u uk u 3 u cos del mismo modo Con esto podemos expresar u u cos i u cos j u cos k u cos i cos j cos k Y además se verifica que cos2 cos2 cos2 1 pues 2 u12 u22 u32 u cos cos cos 2 1 2 u u 2 2 2 Ejemplo 22: Dados los vectores u 2,1,0 y v 1,1,2 calcular: a) El módulo de u y v b) El producto escalar u .v c) el ángulo que forman d) el valor de “m” para que el vector wm,2,3 sea ortogonal con v . e) Hallar la proyección de u sobre v y la de v sobre u Ejemplo 23: Comprobar que los vectores u 1,3,1 y v 0,1,3 son ortogonales y calcular sus módulos Ejemplo 24: Dados los vectores u a,2,2 y v 4, b,3 hallar “a” y “b” para que sea perpendiculares y además v 13 . Ejercicios - 18/22 - A.G.Onandía Geometría: Vectores en el espacio Matemáticas 2 7. Producto vectorial. Definición 19: El producto vectorial de dos vectores u , v V 3 , se denota por u v ó u v , es otro vector que tiene como: 1. módulo el producto de los módulos de u y v por el seno del ángulo que forman i.e. u v u v sen u , v 2. dirección una perpendicular a u y v 3. sentido, el que viene determinado por el avance del sacacorchos que gira de u a v por el camino más corto. De esta definición puede deducirse que: a) si u 0 ó v 0 u v 0 b) si u y v tienen la misma dirección (i.e. son L.D.) entonces u v 0 c) si queremos hallar un vector ortogonal a u y v basta con hallar su producto vectorial. Observación: los vectores cuyo producto escalar es cero son perpendiculares Los vectores cuyo producto vectorial es cero son paralelos 7.1 Interpretación geométrica El módulo del producto vectorial de u y v representa geométricamente el área del paralelogramo que determinan los vectores u y v . u v área del paralelogramo . Demostración: v h u v u v sen u .h base x altura área del parale log ramo h u Obsevación: a) uv senu, v uv u.v cosu, v uv uv tgu, v u.v b) El área de un triángulo de vértices A, B y C es - 19/22 - A.G.Onandía Geometría: Vectores en el espacio Matemáticas 2 Área del triángulo 1 AB AC 2 7.2 Propiedades 3 1. Anticonmutativa: u , v V u v v u 2. Asociativa de la multiplicación de un escalar (homogénea). u , v V 3 , k R k ( u v ) k u v u kv 3. Distributiva respecto a la adición: u , v , w V 3 u (v w) u v u w Ejemplo 25: Comprobar estas propiedades con los vectores: u (1,3,2), v (3,4,1), w(1,5,0) y k 2 7.3 Expresión analítica Tomamos el sistema de referencia 0, i , j , k entonces: u , v V 3 i j u v u1 u2 k u3 con u (u1 , u2 , u3 ); v v1 , v2 , v3 v1 v2 v3 i j k expresión analítica Demostración: u , v V 3 u v u1 u2 v1 v2 u3 desarrolla ndo por la 1ª fila ….(Oxford pag268) v3 Ejemplo 26: Hallar u v . con los vectores u 2,1,0 , v 2,2,1 . Sol. (-1,-2,-6) Ejemplo 27: Dar un vector ortonormal a u 1,1,0 , v 2,3,1 y calcular el área del paralelogramo que determinan. u v 3 3 5 3 , , y Área 3 3 u 2 Sol u v 9 9 9 Ejemplo 28: Hallar el área del triángulo determinado por los puntos: A(1,-2,3), B(3,-1,4) y C(6,-2,1) Sol 110 2 u 2 - 20/22 - A.G.Onandía Geometría: Vectores en el espacio Matemáticas 2 8. Producto mixto El producto mixto es una combinación del p.v. y el p.e.. Definición: Dados tres vectores u , v , w V 3 se define su producto mixto como u.(v w) , en ocasiones se denota u , v , w . 8.1 Expresión analítica En un sistema de referencia 0, i , j , k podemos poner: u , v , w V 3 u1 u .(v w) v1 u2 u3 v2 v3 con u (u1 , u2 , u3 ); v v1 , v2 , v3 ; ww1 , w2 , w3 w1 w2 w3 Expresión analítica Comprobación: v u.(v w ) u1 , u 2 , u 3 2 w2 u1 v2 v3 w2 w3 v3 w3 , u2 v1 w1 v 3 v1 , w 3 w1 v1 v3 w1 w3 u3 v2 w 2 v1 v2 w1 w2 u1 u2 u3 v1 v2 v3 w1 w2 w3 Interpretación geométrica Sean u , v , w V 3 el módulo del producto mixto u .v w es el volumen del paralelepípedo construido sobre ellos. u.v w volumen del paralelepipedo Demostración: u v u h w v paralelepípedo Sea el ángulo formado por u y v w i.e u , v w h u v w v w u cos área de la base por la altura = = área del paralelogramo de la base por la altura = volumen del - 21/22 - A.G.Onandía Geometría: Vectores en el espacio Matemáticas 2 Observación: teniendo en cuenta que Vtetraedro = 1/3 Vprisma triangular Vprisma triangular = 1/2 Vparalelepipedo Podemos deducir que el volumen de un tetraedro es 1 Vtetraedro=1/3 Vprisma triangular=1/6 Vparalelepipedo= u.v w 6 Ejemplo 29: Dados los vectores u 1,1,2, v 1,1,3 y w5,2,1 calcular su producto mixto. Sol -17 Ejemplo 30: Determinar el volumen del paralelepípedo construido sobre los vectores u 1,0,2, v 2,2,2 y w3,1,2 . Sol 10u3. Ejemplo 31: Calcular el volumen del tetraedro cuyos vértices son: A(3,2,5), B(5,-1,4), C(3,-1,-1) y D(4,-3,0). Sol 5/2 Ejercicios - 22/22 - A.G.Onandía


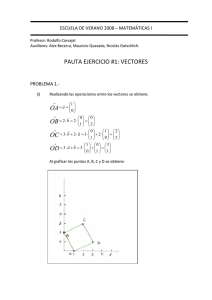



![1 Si v = [ 36 -12 ] , w = [ 9 -3 ] , y S = 1wl. Indique cuáles opciones](http://s2.studylib.es/store/data/004950498_1-7f0b4c506a631255d680bd90dfa0a3e5-300x300.png)