) 90.9cos( 06.0)( ts m tx × × = k M T 3/ 2π = )2/ 2cos( 2)( π +

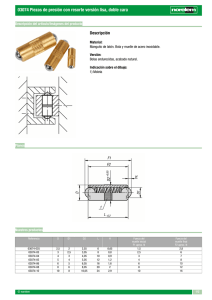
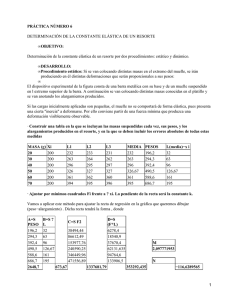
HOJA 1 Problemas de oscilaciones (curso 2013-2014)
Prof. G. Navascués
1.- Un muelle elástico en equilibrio se alarga 10cm al tener colgando una masa de 100 gramos.
Adicionalmente se estira 6 cm desde la posición de equilibrio y en el instante t=0 se suelta. Demostrar
que la posición de la masa en función del tiempo es x(t ) = 0.06m × cos(9.90 s
−1
× t ) para t>0. ¿Cuál es el
máximo cambio de energía cinética que experimenta la masa y entre qué puntos? (Solución: ≈0.0176 J).
2.- Considere dos péndulos de distinta longitud. Uno de ellos tiene un metro de longitud. Determine la
longitud del otro sabiendo que en el mismo tiempo el de 1m de longitud completa 12 oscilaciones
mientras que el otro completa sólo 11 oscilaciones. (Solución: ≈1.19m).
3.- Un muelle elástico cuelga libremente del techo. Se cuelga un objeto del extremo libre y se deja que el
objeto oscile libremente. El máximo alejamiento del extremo que estuvo libre es de 49cm. Determine el
periodo de oscilación. (Solución: ≈0.99s).
4.- Considere el sistema mostrado en la figura que consiste en una barra de longitud L y masa M. En su
centro hay un agujero alrededor del que puede girar sin rozamiento. Un muelle elástico de constante k
está sujeto a un extremo de la barra (su otro extremo está fijo, ver figura). La barra es girada un ángulo
pequeño y a continuación se deja que oscile libremente. Demuestre que el periodo de oscilación es
T = 2π M / 3k .
5.- Considere un muelle elástico vertical sobre una mesa. Se comprime 9.81cm por el efecto de una masa
de 100gr. Si se añaden otros 100gr ¿cuánto se ha comprimido en total? ¿Cuál es la constante elástica del
muelle? (Soluciones: 0.1962m, 10N/M).
6.- Un muelle elástico está sobre una mesa y sujeto por un extremo a una
pared. En el otro extremo tiene una masa de 2kg. Todo ello está en reposo.
Otra masa de 2kg se mueve con una velocidad de 8m/s. En el instante t=0
choca con la masa del muelle, quedan pegadas y empiezan a oscilar. Demuestre que la posición de la
masa total en función del tiempo es x ( t ) = 2m × cos( 2 s × t + π / 2) . Evalúe la energía total del sistema
antes y después de la colisión. (Constante del muelle k=16N/m, las masas se deslizan sin rozamiento).
(Soluciones: 64N/m, 32N/m).
−1
7.- Un tubo en forma de U contiene un liquido (ver figura). La sección del tubo es
A. El líquido ocupa una longitud L del tubo. El líquido es desplazado y a
continuación dejado libremente oscilar. Demuestre que se produce un movimiento
armónico simple y obtenga su periodo. (Solución: T = 2π
L / 2g )
8.- Dos muelles de constantes elásticas k1 y k2 están
la figura. La masa M describe un m.a.s. Demuestre
dispuestos como indica
que
T = 2π M /( k1 + k 2 ) .
9.- Un muelle elástico pende del techo. En su extremo inferior se cuelga una masa que le hace extenderse
9.8cm (posición de equilibrio). A continuación, con la mano, se estira una cantidad adicional y se suelta
produciéndose oscilaciones. Determine el periodo de dichas oscilaciones sabiendo que el coeficiente de
amortiguación logarítmico es λ=3,1. (Solución: 0,70s)
10.- El sistema de la figura consta de una masa, dos muelles elásticos y un
amortiguador hidráulico (M=20kg, k1=50N/m, k2=70N/m y el coeficiente de
amortiguamiento es de 80Ns/m. Determine: A) la posición del centro de masas de
M en función del tiempo, B) El coeficiente de amortiguamiento crítico, indicando el
tipo de amortiguamiento, C) la frecuencia de la vibración libre y la de la vibración
libre amortiguada, D) El valor del periodo y E) si inicialmente la masa se desplaza
de su posición de equilibrio 5cm, la energía mecánica comunicada inicialmente al
sistema indicando si se conserva en el transcurso del movimiento o no.
(Soluciones: x ( t ) = A × e
−2 s × t
sin( 2 s −1 × t + ϕ ) ; bcr≈97.98Ns/m;
6 s −1 ;
2 s −1 ; T = 4.44 s ; E = 0.15 J )