Resortes (Elasticidad)

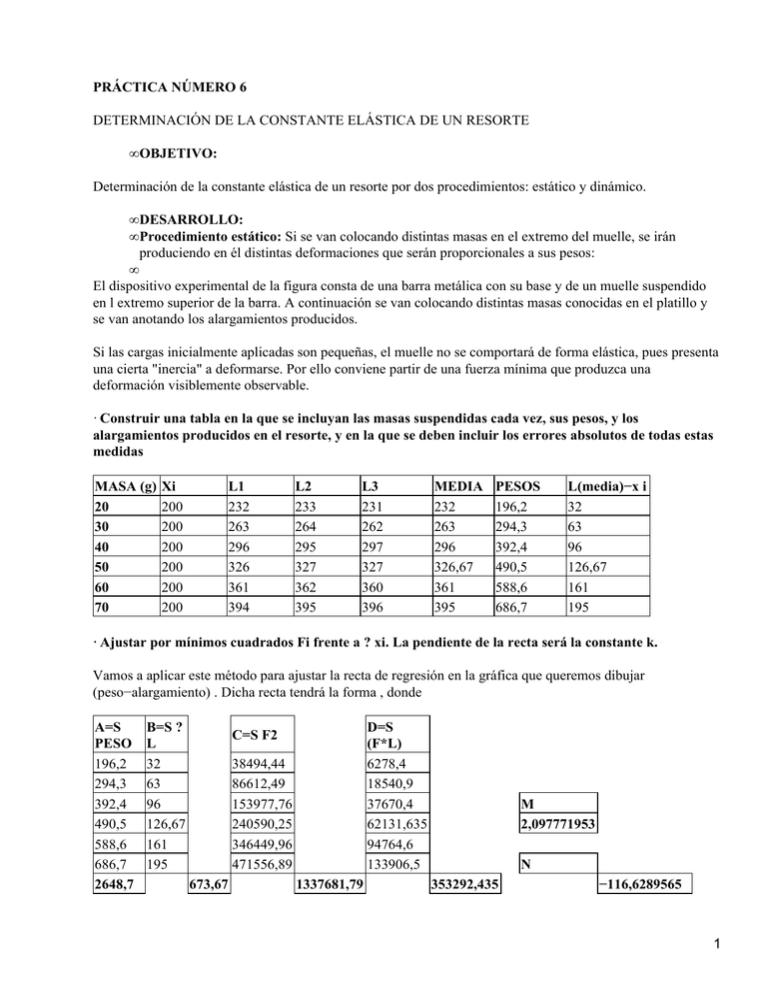
PRÁCTICA NÚMERO 6
DETERMINACIÓN DE LA CONSTANTE ELÁSTICA DE UN RESORTE
• OBJETIVO:
Determinación de la constante elástica de un resorte por dos procedimientos: estático y dinámico.
• DESARROLLO:
• Procedimiento estático: Si se van colocando distintas masas en el extremo del muelle, se irán
produciendo en él distintas deformaciones que serán proporcionales a sus pesos:
•
El dispositivo experimental de la figura consta de una barra metálica con su base y de un muelle suspendido
en l extremo superior de la barra. A continuación se van colocando distintas masas conocidas en el platillo y
se van anotando los alargamientos producidos.
Si las cargas inicialmente aplicadas son pequeñas, el muelle no se comportará de forma elástica, pues presenta
una cierta "inercia" a deformarse. Por ello conviene partir de una fuerza mínima que produzca una
deformación visiblemente observable.
· Construir una tabla en la que se incluyan las masas suspendidas cada vez, sus pesos, y los
alargamientos producidos en el resorte, y en la que se deben incluir los errores absolutos de todas estas
medidas
MASA (g)
20
30
40
50
60
70
Xi
200
200
200
200
200
200
L1
232
263
296
326
361
394
L2
233
264
295
327
362
395
L3
231
262
297
327
360
396
MEDIA
232
263
296
326,67
361
395
PESOS
196,2
294,3
392,4
490,5
588,6
686,7
L(media)−x i
32
63
96
126,67
161
195
· Ajustar por mínimos cuadrados Fi frente a ? xi. La pendiente de la recta será la constante k.
Vamos a aplicar este método para ajustar la recta de regresión en la gráfica que queremos dibujar
(peso−alargamiento) . Dicha recta tendrá la forma , donde
A=S
PESO
196,2
294,3
392,4
490,5
588,6
686,7
2648,7
B=S ?
L
32
63
96
126,67
161
195
D=S
(F*L)
6278,4
18540,9
37670,4
62131,635
94764,6
133906,5
C=S F2
38494,44
86612,49
153977,76
240590,25
346449,96
471556,89
673,67
1337681,79
M
2,097771953
N
353292,435
−116,6289565
1
· Efectuar su representación gráfica dibujando los rectángulos de error
• Procedimiento dinámico: En el mismo dispositivo anterior se requiere determinar el periodo de
oscilación producido tras colocar una determinada masa m en el platillo, la cual debe ser lo
suficientemente grande para que la masa del muelle sea despreciable. Para iniciar la oscilación del
muelle se le somete a un ligero estiramiento con la mano. Las oscilaciones deben producirse en línea
recta y no deben producir movimientos bruscos.
Cada medida ha sido repetida tres veces, contando 50 oscilaciones cada vez, siempre despreciando las
primeras oscilaciones para que las medidas ya se hayan regularizado.
MASA (g)
20
30
40
50
60
70
T1
30,12
35
40,6
44,19
48,19
50,89
T2
29,53
35,17
39,9
43,86
47,46
51,12
T3
29,87
35,24
39,72
43,79
47,45
50,85
MEDIA
29,84
35,13667
40,07333
43,94667
47,7
50,95333
T2
890,426
1234,59
1605,87
1931,31
2275,29
2596,24
Las medidas obtenidas son las siguientes:
A=S Xi
B=S Yi
20
30
40
50
60
70
270
890,426
1234,59
1605,87
1931,31
2275,29
2596,24
10533,73
C= S
X2
400
900
1600
2500
3600
4900
13900
D= S XY
M
17808,52
37037,7
64234,8
96565,5
136517,4
181736,8
533900,72
34,21888571
N
215,7711429
• ¿Qué se consigue en Física determinando una misma magnitud por dos procedimientos
distintos?
Es evidente que el resultado obtenido debe corroborarse aplicando procedimientos distintos puesto que, si
bien cada método puede ser preciso, el error sistemático puede conducir a un deficiente concordancia entre los
resultados. Una elevada concordancia entre los resultados de varios métodos proporciona cierta confianza,
aunque nunca constituye una prueba de que los resultados sean correctos
• ¿Cómo se definiría la oscilación completa?
Se definiría como el espacio recorrido por el cuerpo oscilante entre sus dos posiciones extremas.
2