Procesamiento Digital de Señales

Universidad Nacional de Tucumán
Facultad de Ciencias Exactas y Tecnología
Carrera: Ingeniería Electrónica - Año 2014
Asignatura: PROCESAMIENTO DIGITAL DE SEÑALES (E7S)
Universidad Nacional de Tucumán
Trabajo Práctico Nº2
Tema: Transformada Z
Ejercicio 1:
Demostrar y dar una interpretación gráfica de los teoremas de desplazamiento:
a) Hacia la derecha Z{ f(k-m)}<=> z-m F(z)
b) Hacia la izquierda Z{ f(k+m)}<=> zmF(z) - zm f(0) - ... – z f(m-1)
Demostrar que para m=1, es Z{f(k+1)}= z F(z) - z f(0) ;
Y para m=2, es Z{f(k+2) } =z2F(z) – z2 f(0)- z f(1) ;
Por extensión, deducir que el caso general es:
Z{ f(k+m)}= zmF(z) - zm f(0) – zm-1 f(1) ... – z f(m-1)
Ejercicio 2:
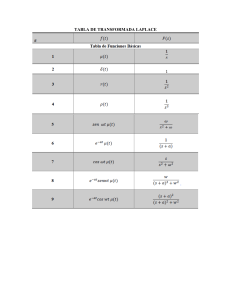
Encontrar, aplicando la definición, la Transformada Z de las siguientes funciones
elementales, y hacer una tabla de las funciones y sus respectivas Transformadas Z:
a) Impulso unitario δ(k), (con δ(k) =1 para k=0; δ(k)=0 para k≠0)
b) Escalón unitario u(k), (con u(k) =1k para k ≥ 0; u(k)=0 para k<0)
c) Escalón alternado û(k), (con û(k)=(-1)k para k ≥ 0; u(k)=0 para k<0)
d) Exponenciales: ak y (-a)k; con k ≥ 0
e) Exponencial compleja y funciones seno y coseno: ejwk, sen(wkT), cos(wkT).
f) Agregar a la tabla los casos de los Teoremas de Desplazamiento a la izquierda: f(k+m)
y a la derecha: f(k-m) demostrados en el Ejercicio 1.
Ejercicio 3:
Aplicando las propiedades y teoremas de la transformada Z, encontrar la función transferencia
H(z-1) del STD asociado a la ecuación de diferencias:
y(k) – a y (k-1) – x(k)=0
Ejercicio 4:
Encontrar la función transferencia H(z-1) del STD asociado a la ecuación de diferencias
general de orden n, aplicando las propiedades y teoremas de la transformada Z.
Ejercicio 5:
Desarrollar los tres métodos de antitransformación, y dar ejemplos de cada caso:
Método 1: Desarrollo de F(z) en Serie infinita de potencias,
Método 2: Desarrollo de F(z) en fracciones parciales,
Método 3: Integral Curvilínea de Cauchy (Suma de los Residuos de F(z). zk-1)