PÉRDIDAS EN LOS DIELECTRICOS - 2º Parte Ing. Francisco R

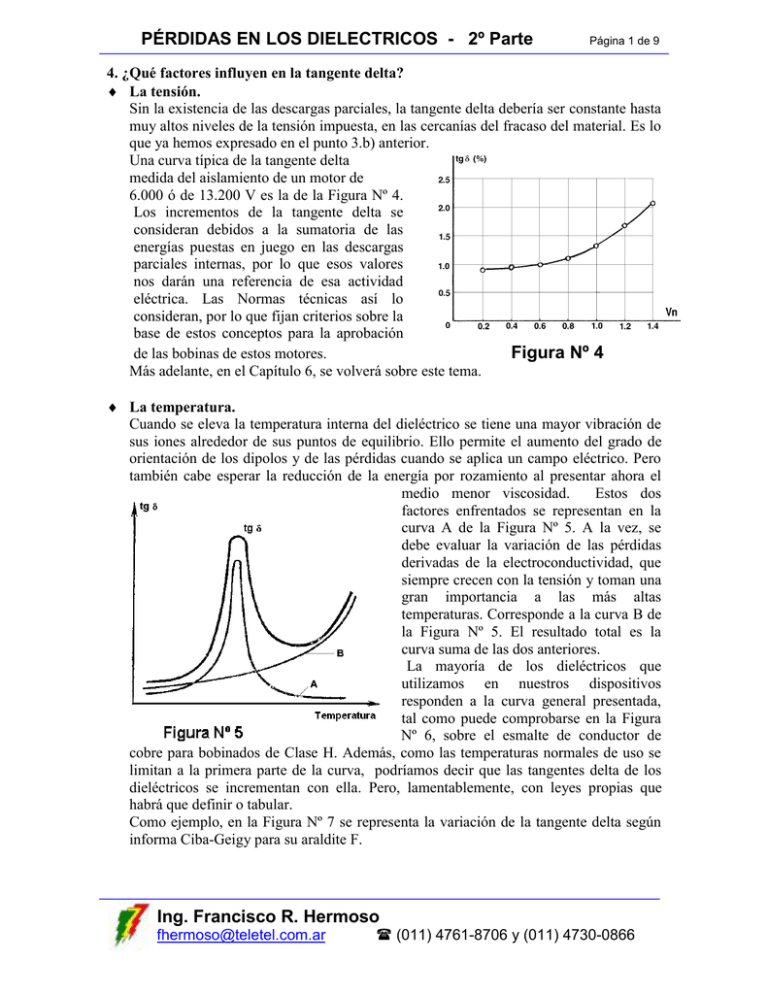
PÉRDIDAS EN LOS DIELECTRICOS - 2º Parte
Página 1 de 9
4. ¿Qué factores influyen en la tangente delta?
La tensión.
Sin la existencia de las descargas parciales, la tangente delta debería ser constante hasta
muy altos niveles de la tensión impuesta, en las cercanías del fracaso del material. Es lo
que ya hemos expresado en el punto 3.b) anterior.
Una curva típica de la tangente delta
medida del aislamiento de un motor de
6.000 ó de 13.200 V es la de la Figura Nº 4.
Los incrementos de la tangente delta se
consideran debidos a la sumatoria de las
energías puestas en juego en las descargas
parciales internas, por lo que esos valores
nos darán una referencia de esa actividad
eléctrica. Las Normas técnicas así lo
consideran, por lo que fijan criterios sobre la
base de estos conceptos para la aprobación
Figura Nº 4
de las bobinas de estos motores.
Más adelante, en el Capítulo 6, se volverá sobre este tema.
La temperatura.
Cuando se eleva la temperatura interna del dieléctrico se tiene una mayor vibración de
sus iones alrededor de sus puntos de equilibrio. Ello permite el aumento del grado de
orientación de los dipolos y de las pérdidas cuando se aplica un campo eléctrico. Pero
también cabe esperar la reducción de la energía por rozamiento al presentar ahora el
medio menor viscosidad.
Estos dos
factores enfrentados se representan en la
curva A de la Figura Nº 5. A la vez, se
debe evaluar la variación de las pérdidas
derivadas de la electroconductividad, que
siempre crecen con la tensión y toman una
gran importancia a las más altas
temperaturas. Corresponde a la curva B de
la Figura Nº 5. El resultado total es la
curva suma de las dos anteriores.
La mayoría de los dieléctricos que
utilizamos en nuestros dispositivos
responden a la curva general presentada,
tal como puede comprobarse en la Figura
Nº 6, sobre el esmalte de conductor de
cobre para bobinados de Clase H. Además, como las temperaturas normales de uso se
limitan a la primera parte de la curva, podríamos decir que las tangentes delta de los
dieléctricos se incrementan con ella. Pero, lamentablemente, con leyes propias que
habrá que definir o tabular.
Como ejemplo, en la Figura Nº 7 se representa la variación de la tangente delta según
informa Ciba-Geigy para su araldite F.
Ing. Francisco R. Hermoso
[email protected]
(011) 4761-8706 y (011) 4730-0866
PÉRDIDAS EN LOS DIELECTRICOS - 2º Parte
Página 2 de 9
Material: TEREBEC 533-34
(Gentileza de IMSA S.A.)
De lo anterior se concluye que en la medición de la tangente delta será siempre
necesario indicar el valor de la temperatura del espécimen.
Y que si se hiciera una comparación entre dos valores medidos a distintas temperaturas
deberíamos conocer la curva correspondiente al material dieléctrico que estamos
analizando.
Muchos fabricantes de elementos electrotécnicos indican en los protocolos de los
ensayos realizados una tabla o curva mostrando cómo varía su tangente delta con la
temperatura de medición. Cuando esas tablas se tienen en la Normas Técnicas, se
refieren a unos ajustes más generales y, por ende, menos exactos. En el Capítulo 6 se
presentan ejemplos de lo expresado.
Por otro lado, cuando en los manuales o escritos se indiquen los valores de las tangentes
delta sin clarificar la temperatura, se debe sobreentender que es la de 20 ºC.
La frecuencia.
La dependencia de la tangente delta con la
frecuencia puede ser observada en la Figura Nº 8,
en la que la escala de las frecuencias del eje x es
logarítmica.
La primera parte de la curva, asintótica con el eje
de ordenadas, se explica porque en las
frecuencias muy bajas las pérdidas por
conducción (medidas con cc. y ocasionadas por
las corrientes debidas a las impurezas), aunque
muy pequeñas, toman ahora importancia ante
valores cercanos a cero de la frecuencia y, por ende, de las corrientes capacitivas. En el
límite tendremos aún una corriente de pérdidas y una nula correspondiente al fenómeno
capacitivo, por lo que la tangente delta tiende a infinito.
Ing. Francisco R. Hermoso
[email protected]
(011) 4761-8706 y (011) 4730-0866
PÉRDIDAS EN LOS DIELECTRICOS - 2º Parte
Página 3 de 9
Sigue luego una porción en que la tangente delta se mantiene prácticamente constante;
se trata del rango de frecuencias en que nosotros trabajamos.
Más allá se pasa a frecuencias en que la molécula entra en resonancia y luego deja de
seguir al campo en su alternancia.
En nuestras mediciones y evaluaciones consideraremos, entonces, que la tangente delta
se mantiene constante y sólo será afectada cuando se tengan presentes frecuencias muy
elevadas.
Quede en claro que al decir que la tangente delta no se modifica prácticamente con la
frecuencia no se afirma que las pérdidas dieléctricas no se elevan con ella, ya que la
frecuencia es uno de los factores que se encuentra multiplicando en las Fórmulas 2 y 4.
La humedad.
Este elemento puede estar presente en los dieléctricos que se analizan, por lo que no
debe ser dejado de lado aunque se lo considere espúreo o indeseable.
Sabemos que la introducción de agua dentro del aislamiento modifica sustancialmente
sus parámetros dieléctricos, desmejorándolos. En el caso que tratamos, incrementará el
valor de la tangente delta en proporción a la humedad que haya absorbido. Porque si
bien crece la corriente capacitiva por la alta permitividad del agua (agua = 81), en
mucho mayor grado se eleva la corriente en fase con la tensión por su extremadamente
alto valor de pérdidas.
El aumento de la tangente delta dependerá, además, de las características físicas del
dieléctrico (por ejemplo, si es fibroso), de la humedad ambiente, de la temperatura de
servicio y de la geometría o condiciones que afectan a la difusión del agua. Es por eso
que no pueden definirse reglas o fórmulas teóricas para utilizar que consideren este
factor como integrante del aislamiento para luego separarlo.
Como los valores de las pérdidas que se agregan con el agua de la humedad son
elevados, un reducido grado de humectación del dieléctrico puede dar valores muy altos
de su tangente delta. En la Figura Nº 9 puede observarse la dependencia de la tangente
delta del papel con la humedad (en % del peso), según D. M. Kazarnovski.
En la siguiente Figura Nº 10 se representa una posible variación de la tangente delta del
aislamiento de un motor de MT cuando se ha humedecido.
Figura Nº 9
Figura Nº 10
Ing. Francisco R. Hermoso
[email protected]
(011) 4761-8706 y (011) 4730-0866
PÉRDIDAS EN LOS DIELECTRICOS - 2º Parte
Página 4 de 9
Por eso, al comparar y analizar dos estados de un mismo dieléctrico deberé
también asegurar que lo estoy observando en iguales o parecidas condiciones de
humectación interior. Para ello conviene utilizar (cotejar) los índices: de absorción
o polarización, que me entrega el megóhmetro en cada una de las mediciones.
Por otro lado, por esta misma característica, es la tangente delta el mejor parámetro a
utilizar para seguir el secado de un aislamiento, controlando la evolución durante la
operación. Tal es el caso de los grandes transformadores.
Aunque resulta obvio conviene indicar que, cuando en los manuales se mencionan los
valores de las tangentes delta de los dieléctricos, se refieren a estados de total sequedad,
sin humedad interior.
Otras contaminaciones.
No es fácil tratarlas a todas y dar estimaciones en cada una de ellas. La diversidad de
casos y grados de contaminación hacen imposible definir reglas o líneas claras de
análisis.
Pero puede decirse que, en general, las contaminaciones superficiales no producen
cambios sustanciales en las tangentes delta; pero sí lo hacen las volumétricas. Ello es
debido a que la contaminación, para ser observada, debe interesar a una importante
porción de la masa total del aislamiento, que es la que aporta el valor de la tangente
delta.
A modo de ejemplo se comenta que es posible encontrar aislamientos de motores de
MT impregnados con aceite lubricante que ha escapado de los cojinetes. En estos casos
pueden medirse niveles de tangente delta de los arrollamientos muy superiores a los
normales de los dieléctricos utilizados. El autor ha encontrado en esos casos valores de
la tangente delta de 30 % y superiores.
El tiempo.
Pensar en la influencia del tiempo sobre la tangente delta de un dieléctrico es lo mismo
que analizar su degradación o envejecimiento a través de este parámetro.
Figura Nº 11
Figura Nº 12
Ing. Francisco R. Hermoso
[email protected]
(011) 4761-8706 y (011) 4730-0866
PÉRDIDAS EN LOS DIELECTRICOS - 2º Parte
Página 5 de 9
En los aislamientos sólidos lo hace incrementando sus valores (desmejorando su
condición de dieléctrico) y adelantando el “codo” que se produce en su curva en
función de la tensión. En la Figura Nº 11 se muestra una variación que podría esperarse
en un aislamiento luego de 100.000 horas de servicio. Sin embargo, por no poder fijar
con total precisión las condiciones en que opera nuestro aislamiento en el servicio
(temperatura, contaminaciones, solicitaciones eléctricas, etc.), no pueden indicarse
reglas o fórmulas fijas valederas para todos los casos que definan las velocidades de los
cambios.
En la Figura Nº 12 se muestra la variación de la tangente delta que se tendría en un
transformador con aceite aislante mineral que no tiene inhibidor de su oxidación. El
ejemplo ha sido tomado del libro “Transformerboard” de H. P. Moser.
Los altos valores a que se arriban en corto tiempo explican el esfuerzo dirigido a estos
aspectos en los desarrollos actuales de los aceites.
Las clases térmicas.
La capacidad de un dieléctrico para soportar la temperatura de servicio no tiene ninguna
relación con los valores de su tangente delta.
Y así podemos constatar que el aceite mineral aislante utilizado en los transformadores,
de Clase A (105 ºC), presenta una tangente delta muy reducida, del orden de 0.40 %, tal
como se verá más adelante.
Pero sí es cierto que en los aislamientos sólidos es común encontrar valores más altos
de la tangente delta en las clases térmicas menores: E (120 ºC ) y B (130 ºC), que en las
F (155 ºC) y H (180 ºC). Ello se debe a que las primeras eran las más usadas en las
máquinas de BT y/o de menor envergadura, generalmente con exigencias dieléctricas
inferiores a las que luego se han diseñado en las de Clase F o superiores. Ello
permite la utilización de dieléctricos de menor “calidad” en este aspecto, lo que estaría
en parte justificado por el análisis que se verá en el punto siguiente.
5. Consideraciones relativas a la falla de un dieléctrico.
Para entender y justificar el control de la tangente delta de los aislamientos conviene
analizar las causas que producen su fracaso y observar qué vinculación tienen con aquélla.
En otras palabras, dado que nuestro trabajo principal es preservar el dieléctrico, haciendo
que se mantenga en buenas condiciones por el mayor tiempo posible, debemos instruirnos
entonces sobre las causas de la pérdida de su rigidez dieléctrica y analizar su relación con la
tangente delta.
Las agresiones que sufre un dieléctrico en servicio y que van produciendo su degradación
se presentan como una combinación de:
-
Eléctricas, derivadas por los campos internos y las descargas parciales, sobre los que
hemos hablado;
-
Térmicas, porque el dieléctrico envejece más rápidamente cuanto mayor es su
temperatura;
-
Mecánicas, por vibraciones propias y de las máquinas asociadas, que producen
movimientos relativos entre las distintas partes, derivando luego en erosión mecánica y
debilitamiento del aislamiento;
Ing. Francisco R. Hermoso
[email protected]
(011) 4761-8706 y (011) 4730-0866
PÉRDIDAS EN LOS DIELECTRICOS - 2º Parte
-
Página 6 de 9
Químicas, por acción de agentes líquidos o gaseosos que atacan al dieléctrico.
Como no es posible estudiar la respuesta de cada dieléctrico a las infinitas posibilidades de
las agresiones presentadas, se analizan y buscan leyes que muestren las acciones
individuales o con un número muy limitadas de ellas. En nuestro caso sólo vamos a tratar
las dos primeras, porque son las que más están relacionadas con la tangente delta.
A pesar que los físicos aún siguen investigando los mecanismos de las fallas de los
dieléctricos sólidos y aceptan diversas causas concurrentes no del todo aclaradas, hay
consenso en decir que se tienen dos tipos:
-
-
La falla intrínseca o puramente eléctrica, que se produce en lapsos muy cortos de
aplicación de la tensión (inferiores al segundo). Considera que la solicitación eléctrica
interna (por acción del choque de partículas fuertemente aceleradas por el campo
eléctrico) es suficiente para que en ciertos puntos se destruya el andamiaje estructural y
que el dispositivo se caiga luego completamente.
Los valores de las tensiones que definen este tipo de falla no dependen del tiempo de
aplicación, ni de la frecuencia; sólo del valor máximo o de cresta.
La falla térmica, que se produce por acumulación de una energía térmica que se
desarrolla en un punto o zona, como producto de las pérdidas dieléctricas y el tiempo, y
causa un deterioro local suficiente como para que el resto del dispositivo aislante no
soporte las solicitaciones posteriores y colapsar totalmente. En este tipo de falla, la
rigidez dieléctrica de mi aislamiento está fuertemente asociada a su “historia”, es decir,
a la suma de las solicitaciones anteriores que han ido acumulando o agrandando la zona
afectada.
Figura Nº 13
En la Figura Nº 13 se muestra una
representación de la curva de la tensión
posible a soportar por un aislamiento sólido o
de un dispositivo aislante, mostrando las áreas
de los dos tipos de fallas explicadas.
Las investigaciones también coinciden en
afirmar que cualquiera de las fallas anteriores
en los dieléctricos sólidos se producen en
puntos singulares o de fuertes imperfecciones,
en donde se concentran intensos campos por
impurezas y/o importantes distorsiones del
material. Es decir, zonas donde las pérdidas
específicas, las que podrían evaluarse según
la Fórmula Nº 4 de conocerse todos los
parámetros involucrados, son extremadamente altas, muy diferentes a la valoración media o
promedio que surge de la tangente delta. Porque, sin la presencia de estos puntos o
debilidades acentuadas no cabría pensar en la falla de los dieléctricos a las tensiones que
comprobamos que ocurren en la realidad. Es así: las tensiones reales necesarias para romper
la estructura interna del material o forzar un camino conductor en un aislante sólido son
muy inferiores a las que surgen de los cálculos teóricos.
Ing. Francisco R. Hermoso
[email protected]
(011) 4761-8706 y (011) 4730-0866
PÉRDIDAS EN LOS DIELECTRICOS - 2º Parte
Página 7 de 9
Algunas líneas modernas de investigación analizan las formas posibles de las distribuciones
de los distintos estados energéticos de la masa del dieléctrico para lograr una evaluación
más realista. Podrá inferir el lector que esa pretendida distribución estará muy relacionada
con el proceso tecnológico de conformación de nuestro aislamiento y no podrá ser definida
fácilmente en forma anticipada y/o general.
La clara diferenciación en los dos tipos de fallas, que es muy representativo en los
dieléctricos sólidos, es menos observable en los fluidos. El segundo tipo de descarga, la
térmica, en el punto o zona con altas pérdidas puede producir fuertes corrientes y
movimientos del fluido que lo hacen cambiante permanentemente, pero siempre reduciendo
la posibilidad de propagar el deterioro a las zonas adyacentes. Es por ello que para estos
materiales: gases y líquidos, se entiende que la falla está más asociada a la del tipo
intrínseco.
Obviamente, por ser la tangente delta del dieléctrico un parámetro relacionado con los
procesos de las pérdidas internas, ella se encontrará ligada con el segundo tipo de descarga
que hemos llamada térmica.
La explicación física del fenómeno dice que, en ciertos puntos singulares, la masa del
aislamiento no puede llegar a erradicar (o transmitir hacia el exterior o a otras zonas) las
pérdidas que se generan en su interior, aumentando su temperatura. Ello, a su vez, produce
el incremento de esas pérdidas y así sucesivamente hasta el colapso.
La comprensión cabal del fenómeno es más fácil mediante fórmulas. Pero, el tratamiento
teórico y numérico es sumamente complejo; es más sencillo analizarlo en forma gráfica.
La Fórmula Nº 4 nos daba el valor de las pérdidas específicas o por volumen, es decir las
que se producían en su interior.
pca. = 2 f o r tg E2
Esa misma masa de dieléctrico tiene una capacidad para transmitir esa energía y evacuarla
que puede ser expresada como:
pca. = (A/Vol.) ( T - To )
Siendo:
A (en m2) es el área a través de la cual se conduce la energía;
Vol. (en m3) es el volumen en donde se producen las pérdidas;
(en Wm/m2ºC) es el coeficiente de transmisión térmica del material;
(T – To) es la diferencia de temperaturas necesaria para transmitir las pérdidas, la que se
tendría entre los dos planos extremos (de A m2) del volumen V.
Las dos fórmulas anteriores deben igualarse para así encontrar los puntos de equilibrio en
que se satisfacen ambas.
En la Figura Nº 14 se han representado las pérdidas específicas en función de la
temperatura en forma paramétrica, para varios valores del campo eléctrico E.
Las curvas responde a la forma expuesta en el Capítulo 4 (La temperatura) con sus
comentarios.
Por otro lado la recta representa la segunda fórmula: la capacidad del dieléctrico para
conducir esa energía hacia las adyacencias, siendo el coeficiente de transmisión del calor
del dieléctrico.
Ing. Francisco R. Hermoso
[email protected]
(011) 4761-8706 y (011) 4730-0866
PÉRDIDAS EN LOS DIELECTRICOS - 2º Parte
Página 8 de 9
La figura muestra que para zonas con
campos inferiores al Ec crítico se
alcanzan siempre puntos de equilibrio,
por encima de los cuales, incluso, la
posibilidad de evacuación de las pérdidas
es superior a la de su generación. Por
ejemplo, para el campo E1 < Ec le
corresponde la temperatura indicada T1.
En cambio, para los puntos con campos
eléctricos superiores al Ec la curva de las
pérdidas dieléctricas se incrementa
mucho más rápido que la recta que
muestra su disipación, llevando al
dieléctrico al fracaso. (Las ordenadas
correspondientes
a
las
pérdidas
generadas son mayores a las posibles a
Figura Nº 14
trasmitir por conducción).
El campo crítico Ec , con su temperatura de equilibrio Tc, es el máximo valor que podemos
tener para que el proceso sea estable, controlado.
Para comprender mejor y más cabalmente lo representado cabe mencionar que:
La temperatura To corresponde a la del servicio del aislamiento, la que se encuentra
definida por el calentamiento derivado del rendimiento de nuestra máquina y el
ambiente. Por lo que podrá ser cambiante al modificarse alguna de esas condiciones.
Es la temperatura de la que parte el proceso que analizamos. En las máquinas eléctricas
se habla de un calentamiento medio en todo el arrollamiento, pero la temperatura
interior es variable en un grado tal que la Norma presume que podrían haber zonas que
superen ese promedio y lleguen a los límites fijados para su Clase de Aislación
Térmica.
Por ejemplo: para una máquina rotante aislada en Clase F, se especifica un
calentamiento máximo (medio para todo el arrollamiento) de 105 ºC sobre una de
ambiente de 40 ºC, lo que da un total de 145 ºC de temperatura, cuando el límite de la
Clase es 155 ºC. Nosotros debemos esperar, entonces, que algunas partes de mi
aislamiento podrían llegar a tener esta temperatura límite de 155 ºC, es decir, que para
esos puntos ese es el valor de To que podríamos considerar.
La pendiente de la recta de la conducción térmica se encuentra definida especialmente
por su coeficiente de transmisión y sería fija para un aislamiento determinado.
Cuanto mayor sea el grado de irregularidad eléctrica mayor será la posibilidad de tener
zonas proclives a una catástrofe térmica como la presentada.
Por último, cabe agregar que en la representación de la curva de las pérdidas específicas
en función de la temperatura de nuestro dieléctrico se ha considerado constante la
frecuencia. En el caso de tener fenómenos en los que puedan aparecer otras de más altos
niveles: armónicos en la tensión de alimentación o lo expuesto en el punto 3.e) anterior
relativo a las descargas parciales internas, deberemos asumir que la curva de las
Ing. Francisco R. Hermoso
[email protected]
(011) 4761-8706 y (011) 4730-0866
PÉRDIDAS EN LOS DIELECTRICOS - 2º Parte
Página 9 de 9
pérdidas tendrá una forma de crecimiento más rápido aún, haciendo más crítica la
situación.
Cabe que el lector inquieto indague sobre si la representación física del colapso térmico,
que se explica mediante unas curvas generales entre ejes sin escalas de la Figura Nº 14, se
ajusta a los niveles de los campos eléctricos que tenemos en nuestros aislamientos. Ello es
así. Análisis teóricos, apoyados en suposiciones matemáticas de las formas de la curva de
las pérdidas específicas en función de la temperatura, llegan a la conclusión que el modelo
físico presentado es válido. En el Capítulo 21: “Calentamiento de los aislantes sólidos por
efecto de las pérdidas dieléctricas”, del libro “Técnicas de la Alta Tensión” del Dr. Ing.
Arnold Roth,, se trata el tema y se presentan ejemplos y verificaciones, repetidos luego por
el Ing. J. Corrales Martín en su libro “ Cálculo Industrial de Máquinas Eléctricas”.
Las altas diferencias entre los campos eléctricos posibles de encontrar en los dispositivos
aislantes que fueron comentados en el Capítulo 3 indican la clara posibilidad de tener esos
puntos propensos a calentamientos exagerados.
Podemos afirmar, entonces, que el incremento del valor total o medio de la tangente
delta va marcando el escalón en donde se apoya el proceso indeseado de la falla
térmica.
------------------------------Como podrá observar, caro lector, este escrito se ha dividido en tres partes en lugar de las
dos de la idea original.
Ello se ha debido a los pedidos recibidos de detallar aspectos que hemos considerado
valederos.
Con la tercera parte se completa el tema.
Ing. Francisco R. Hermoso
[email protected]
(011) 4761-8706 y (011) 4730-0866