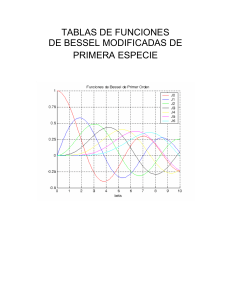
Propiedades de las funciones de Bessel: Jn(x)=(-1)nJn(x)
Anuncio

Métodos matemáticos III Alberto Martín Pérez Propiedades de las funciones de Bessel: J-n(x)=(-1)nJn(x) Para demostrar esta propiedad se tendrá en cuenta la forma en serie de potencias de las funciones de Bessel: +∞ 𝐽𝑚 (𝑥 ) = � 𝑠=0 𝑥 𝑚+2𝑠 (−1)𝑠 � � 𝑠! (𝑚 + 𝑠)! 2 Para una función de Bessel de orden negativo se tendrá: +∞ 𝐽−𝑛 (𝑥 ) = � 𝑠=0 𝑥 −𝑛+2𝑠 (−1)𝑠 � � 𝑠! (−𝑛 + 𝑠)! 2 A continuación se hace el cambio de índice del sumatorio j=s-n. +∞ +∞ (−1)𝑗+𝑛 𝑥 −𝑛+2(𝑗+𝑛) (−1)𝑗 (−1)𝑛 𝑥 2𝑗+𝑛 � � =� � � 𝐽−𝑛 (𝑥 ) = � (𝑗 + 𝑛)! 𝑗! 2 (𝑗 + 𝑛)! (−𝑛 + 𝑗 + 𝑛)! 2 𝑠=0 = (−1)𝑛 𝐽𝑛 (𝑥) 𝑠=0 Por lo tanto, queda demostrado que 𝐽−𝑛 (𝑥) = (−1)𝑛 𝐽𝑛 (𝑥). Bloque 3