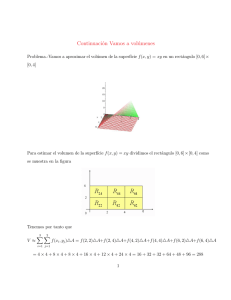
Teorema 1. Sea f

Teorema 1. Sea f : R ⊂ Rn → R integrable sobre R. Entonces existe x0 ∈ (R) tal que f es
continua en x0
Demostración. Como f es integrable ∃ una patición P de R tal que
S(f, P ) − S(f, P ) =
m X
n
X
Mij A(Rij ) −
i=1 j=1
m X
n
X
mij A(Rij ) =
i=1 j=1
m X
n
X
(Mij − mij )A(Rij ) < A(R)
i=1 j=1
Como los términos de la suma son no negativos ∃ subindices i, j que sin perdida de generalidad
podemos suponer que son 11 para los cuales
M11 − m11 < 1
Pues de lo contrario si Mij − mij ≥ 1 ∀i, j entonces
Mij − mij ≥ 1 ⇒ (Mij − mij )(A(Rij )) ≥ A(Rij ) ⇒
m X
n
X
(Mij − mij )A(Rij ) ≥
i=1 j=1
m X
n
X
A(Rij )
i=1 j=1
⇒ S(f, P ) − S(f, P ) ≥ A(R)
lo cual no puede ocurrir pues escogimos P de tal forma que
S(f, P ) − S(f, P ) < A(R)
LLamo R1 al subrectángulo inducido por P para el cual se satisface
M11 − m11 < 1 y
R1 ⊂ int(R)
como f es integrable en R, entonces f es integrable en R1 .
Tomamos ahora P1 partición de R1 tal que
S(f, P ) − S(f, P ) =
m X
n
X
(Mij − mij )A(Rij ) <
i=1 j=1
A(R1 )
2
Procediendo de manera analoga ∃ R2 subrectángulo inducido por P1 sobre R1 para el cual
M22 − m22 <
1
2
con R2 ⊂ Int(R1 )
1
siguiendo este procedimiento obtenemos una sucesión {Rk } de rectángulos anidados en Rn con
la propiedad
Mk − mk <
1)
2
Rk+1 ⊂ Rk
1
k
∀k ∈ N
Por el teorema de rectángulos anidados
n
\
Rk 6= ∅
1
Si x0 ∈
Tn
1
Rk probaremos que f es continua en x0
Sea > 0 y N ∈ N tal que
1
N
< como x0 ∈ Rn+1 ⊂ Int(Rk ) ∃ δ > 0 tal que
Bδ (x0 ) ⊂ Int(RN ) ⊂ RN
donde mn ≤ f (x) ≤ MN
∀x ∈ Bδ (x0 )
como
MN − mN <
1
N
entonces |f (x) − f (x0 )| <
∴ f es continua en x0
2
1
< ε ∀x ∈ Bδ (x0 )
N