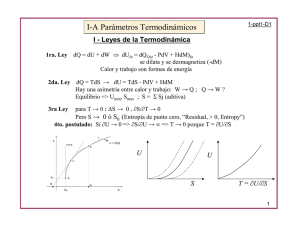
F U TS = − G U TS pV F pV H TS = − + = + = − U H U pV F U TS G U

TERMODINÁMICA FUNDAMENTAL
TEMA 7. Potenciales termodinámicos
1. Potenciales termodinámicos
1.1. Potenciales termodinámicos en sistemas simples PVT
Hasta el momento hemos visto dos funciones energéticas de estado: la energía interna, U, y la entalpía, H. Vamos a
definir dos nuevas funciones energéticas de estado, que junto con U y H formarán lo que se conoce como funciones
termodinámicas o potenciales termodinámicos.
Función de Helmholtz o Energía Libre: Se define como
F = U − TS
Función de Gibbs, Entalpía libre o Energía libre de Gibbs: Se define como
G = U − TS + pV = F + pV = H − TS
Así, los cuatro potenciales termodinámicos son:
U
H = U + pV
F = U − TS
G = U − TS + pV
Utilizando la forma entrópica del primer principio,
dU = TdS − pdV
podemos escribir las formas diferenciales de los potenciales termodinámicos, en función de las variables p, V, T y S:
dU = TdS − pdV
dH = dU + pdV + Vdp = TdS + Vdp
dF = dU − TdS − SdT = − SdT − pdV
dG = dU − TdS − SdT + pdV + Vdp = − SdT + Vdp
Las variables independientes en estas expresiones, para cada potencial termodinámico determinado, son sus variables
naturales. Así, en función de sus variables naturales, los potenciales se expresarían como:
U = U ( S ,V )
H = H ( S , p)
F = F (T , V )
G = G (T , p )
1.2. Relaciones de Maxwell
A partir de las formas diferenciales de los potenciales termodinámicos, surge una manera muy sencilla de relacionar
las derivadas parciales de estos potenciales (en función de sus variables naturales), con las otras variables:
 ∂U 
 ∂U 
T =
 ; p = −

 ∂S V
 ∂V  S
 ∂H 
 ∂H 
T =

 ;V = 
 ∂S  p
 ∂p  S
 ∂F 
 ∂F 
S = −
 ; p = −

 ∂T V
 ∂V T
 ∂G 
 ∂G 
S = −

 ;V = 
 ∂T  p
 ∂p T
estas igualdades se conocen como relaciones de orden cero.
Apliquemos ahora la regla matemática según la cual las derivadas cruzadas de una función son independientes del
orden de derivación:
Para la función U, tenemos
 ∂ 2U 
 ∂ 2U  

 =
 
 ∂V ∂S V , S  ∂S ∂V  S ,V 

 ∂ 2U 
  ∂T 
 ∂T 
 ∂p 
⇒

 =

 = − 
 ∂S V
 ∂V ∂S V , S  ∂V  S
  ∂V  S

 ∂ 2U 
 ∂p 


 = − 

∂
∂
∂
S
V
S



 S ,V
V

Para H:
 ∂2H 
 ∂2 H  

 =
 
 ∂p∂S  p , S  ∂S ∂p  S , p 

 ∂2H 
 ∂T 
  ∂T   ∂V 
⇒

 =

 =

 ∂p∂S  p , S  ∂p  S
  ∂p  S  ∂S  p

 ∂2H 
 ∂V 


 =


∂
S
∂
p
∂
S



S , p
p

Para F:
 ∂2 F 
 ∂2 F  

 =
 
 ∂V ∂T V ,T  ∂T ∂V T ,V 

 ∂2 F 
  ∂S   ∂p 
 ∂S 
⇒

 = −

 =

 ∂V T   ∂V T  ∂T V
 ∂V ∂T V ,T

 ∂2 F 
 ∂p 


 = −

 ∂T V 
 ∂T ∂V T ,V
Finalmente, para G:
 ∂ 2G 
 ∂ 2G  
=



 
 ∂p∂T  p ,T  ∂T ∂p T , p 

 ∂ 2G 
 ∂S 
  ∂S 
 ∂V 
 ⇒   = −

 = − 

 ∂T  p
 ∂p T   ∂p T
 ∂p∂T  p ,T

 ∂ 2G 
 ∂V 


 =


∂
T
∂
p
∂
T


p

T , p

Las cuatro relaciones que nos quedan, son las relaciones de primer orden, conocidas como relaciones de Maxwell:
 ∂T 
 ∂p 

 = − 
 ∂V  S
 ∂S V
 ∂T   ∂V 

 =

 ∂p  S  ∂S  p
 ∂S   ∂p 

 =

 ∂V T  ∂T V
 ∂S 
 ∂V 
  = −

 ∂T  p
 ∂p T
Podemos observar tres características que se cumplen en estas cuatro relaciones:
1. Los productos cruzados tienen dimensiones de energía y son de la forma [TS]=[pV].
2. La variable independiente en el denominador de un miembro es la constante en el otro.
3. El signo es positivo si T y p están asociadas (o S y V) y negativo si no es así (T con V y S con p).
1.3. Significado físico de los potenciales termodinámicos
Función de Helmholtz:
Sea una transformación monoterma de un sistema, desde el estado 1 hasta el 2, donde la única fuente con la que hay
intercambio de calor está a una temperatura T0. Según el primer principio, el trabajo es
W = −∆U + Q = (U1 − U 2 ) + Q
Por el segundo principio:
∆SU = ∆S + ∆S F ≥ 0 
Q

−Q
 → ( S 2 − S1 ) − ≥ 0 → T0 ( S 2 − S1 ) ≥ Q
∆S F =
T0

T0

Sustituyendo esto en la ecuación del trabajo:
W ≤ (U1 − U 2 ) + T0 ( S2 − S1 ) = (U1 − T0 S1 ) − (U 2 − T0 S 2 )
Como la temperatura inicial y final del sistema es T0, tenemos que
W ≤ F1 − F2 ⇒ W = −∆F
Cuando un sistema experimenta un proceso monotermo, el trabajo producido es menor o igual que la disminución de
la energía libre de Helmholtz del sistema.
Si el proceso es reversible, el trabajo alcanza su valor máximo:
Q = T0 ∆S → W = Wmax = −∆F
Igualmente, el trabajo mínimo (negativo) en valor absoluto requerido para producir un determinado cambio de estado
es:
Wmin = (U 2 − U1 ) − T0 ( S2 − S1 ) = F2 − F1 = ∆F
Podemos decir que la energía interna se compone de dos términos:
U = F + TS
El primero es la energía libre, que puede convertirse íntegramente en trabajo. El segundo término se llama
termentropía y no puede transformarse en trabajo.
La función F desempeña en los procesos monotermos el mismo papel que la energía interna en los adiabáticos, ya
que:
Wad = −∆U
Función de Gibbs:
Sea una transformación monoterma (T0) y monobara (presión externa constante, p0, e igual a la inicial y a la final) de
un sistema, desde el estado 1 hasta el 2. Según el primer principio, el trabajo es
W = Wdil + Wnd = −∆U + Q → Wnd = −∆U + Q − p0 ∆V
donde hemos dividido el trabajo en trabajo de dilatación, Wdil, y en trabajo distinto al de dilatación, Wnd.
Como el proceso es monotermo, podemos proceder como hemos hecho al estudiar la función F, con lo cual:
Wnd ≤ (U1 − U 2 ) − T0 ( S1 − S2 ) + p0 (V1 − V2 ) = (U1 − T0 S1 + p0V1 ) − (U 2 − T0 S2 + p0V2 ) = ( G1 − G2 )
Es decir:
Wnd ≤ −∆G
En un proceso monotermo y monobaro, la disminución de la función de Gibbs mide el máximo trabajo distinto del de
dilatación que se puede obtener en dicha transformación.
Cuando el único trabajo es el de dilatación:
0 ≤ −∆G → ∆G ≤ 0 → G2 ≤ G1
La función G permanece constante (proceso isotermo e isobaro) o disminuye (proceso monotermo y monobaro
irreversible).
Análogamente a lo que hemos hecho en el caso de F, podemos dividir la entalpía en dos términos:
H = G + TS
la energía libre de Gibbs o entalpía libre y la termentropía.
2. Condiciones de equilibrio y estabilidad
El análisis de los potenciales termodinámicos permite deducir el sentido de un proceso y sus condiciones de
equilibrio. Consideremos procesos monotermos y monobaros:
Wnd ≤ (U1 − U 2 ) − T0 ( S1 − S 2 ) + p0 (V1 − V2 ) = (U1 − T0 S1 + p0V1 ) − (U 2 − T0 S 2 + p0V2 ) = ( G1 − G2 )
Si el proceso es infinitesimal y el único trabajo es de dilatación:
T0 dS ≥ dU + p0 dV
Podemos llegar al mismo resultado partiendo de la desigualdad de Clausius:
dS ≥
∂Q dU + p0 dV
=
T
T0
Si el proceso es reversible:
TdS = dU + pdV
Si restringimos el proceso irreversible imponiendo que dos de las variables termodinámicas (p, V, T, S, U)
permanezcan sean iguales al principio y al final, simplificamos la desigualdad anterior.
•
Sistema aislado:
dU = dV = 0 → dS ≥ 0
La entropía de un sistema aislado crece en todo proceso irreversible y es constante en el reversible. En el equilibrio,
la entropía ha de ser máxima:
( dS ) = 0; ( d 2 S ) < 0
•
Sistema isoentrópico y mecánicamente aislado:
dS = dV = 0 → dU ≤ 0
La energía interna disminuye. En el equilibrio es mínima:
( dU ) = 0; ( d 2U ) > 0
•
Sistema isoentrópico y en equilibrio mecánico con el medio:
dS = 0; p = p0 → dU + pdV = dH ≤ 0
La entalpía disminuye. En el equilibro es mínima:
( dH ) = 0; ( d 2 H ) > 0
•
Sistema en equilibrio térmico con el medio y mecánicamente aislado:
dV = 0; T = T0 → dU − TdS = dF ≤ 0
La energía libre de Helmholtz disminuye. En el equilibrio es mínima:
( dF ) = 0; ( d 2 F ) > 0
•
Sistema en equilibrio término y mecánico con el medio:
T = T0 ; p = p0 → dU − TdS + pdV = dG ≤ 0
La energía libre de Gibbs disminuye. En el equilibrio es mínima:
( dG ) = 0; ( d 2G ) > 0
3. Ecuaciones TdS
A partir de las relaciones de Maxwell, podemos expresar la entropía (en forma diferencial) en función de dos de las
variables p, V y T. De esta forma, vamos a obtener tres relaciones muy útiles a la hora de calcular las propiedades de
sistemas en los procesos termodinámicos que experimentan, las ecuaciones TdS.
3.1. Ecuaciones TdS
En función de T y V:
1  T ∂S 
1  ∂Q 
 ∂S 
 ∂S 
 ∂p 
 ∂p 
dS = 
 dT + 
 dV = 
 dT + 
 dV = 
 dT + 
 dV
T  ∂T V
T  ∂T V
 ∂T V
 ∂V T
 ∂T V
 ∂T V
1 ( ∂Q )V
CV
 ∂p 
 ∂p 
 ∂p 
⇒ dS = ⋅
dT + 
dT + 
 dV =
 dV → TdS = CV dT + T 
 dV
T dT
T
 ∂T V
 ∂T V
 ∂T V
En función de T y p:
 ∂S 
1  T ∂S 
1  ∂Q 
 ∂S 
 ∂V 
 ∂V 
dS = 
 dT +   dp = 
 dT − 
 dp = 
 dT − 
 dp
T  ∂T  p
T  ∂T  p
 ∂T  p
 ∂T  p
 ∂T  p
 ∂p T
Cp
1 ( ∂Q ) p
 ∂V 
 ∂V 
 ∂V 
⇒ dS = ⋅
dT − 
dT − 
 dp =
 dp → TdS = C p dT − T 
 dp
T dT
T
 ∂T  p
 ∂T  p
 ∂T  p
En función de p y V:
 ∂S 
T  ∂S  dT
T  ∂S  dT
 ∂S 
dS =   dp + 
dp + 
dV
 dV =  

T  ∂p V dT
T  ∂V  p dT
 ∂V  p
 ∂p V
⇒ dS =
 ∂T 
 ∂T 
1  ∂Q   ∂T 
1  ∂Q   ∂T 
1
1
 dp + 
 dV = CV 
 dp + C p 
 dV

 
 
T  ∂T V  ∂p V
T  ∂T  p  ∂p V
T
T
 ∂p V
 ∂p V
⇒ TdS = CV dT + C p dV
Recapitulando, las ecuaciones TdS son:
 ∂p 
TdS = ncV dT + T 
 dV
 ∂T V
 ∂V 
TdS = nc p dT − T 
 dp
 ∂T  p
 ∂T 
 ∂T 
TdS = ncV 
 dp + nc p 
 dV
 ∂V  p
 ∂p V
Considerando la forma entrópica del primer principio:
 ∂U 
 ∂U 
dU = TdS − pdV → TdS = dU + pdV = 
 dT + 
 dV + pdV
 ∂T V
 ∂V T
 ∂U 

⇒ TdS = ncV dT + 
 + p  dV
 ∂V T

Comparando este resultado con la primera ecuación TdS:
 ∂U 
 ∂p 
 ∂U 
 ∂p 

 + p =T 
 →
 =T 
 −V
 ∂V T
 ∂T V
 ∂V T
 ∂T V
 ∂U 
Podemos determinar la propiedad energética 
 para cualquier sistema.
 ∂V T
Análogamente, utilizando la forma diferencial de la entalpía y la segunda ecuación TdS:
 ∂H 
 ∂H 
dH = TdS + Vdp → TdS = dH − Vdp = 
 dp − Vdp
 dT + 
 ∂T  p
 ∂p T
 ∂H 

 ∂V 
⇒ TdS = nc p dT + 
−
V
 dp = nc p dT − T 

 dp
 ∂T  p
 ∂p T

 ∂H 
 ∂H 
 ∂V 
 ∂V 
⇒
 − V = −T 
 = −T 
 →
 +V
 ∂T  p
 ∂T  p
 ∂p T
 ∂p T
 ∂H 
Podemos determinar la propiedad energética 
 para cualquier sistema.
 ∂p T
3.2. Ecuación generalizada de Mayer
Con los resultados que acabamos de obtener, vamos a reescribir la ecuación de Mayer generalizada:
 ∂U 

TV α 2
 ∂p 
α
α
β
α
C p = CV + 
+
p
V
=
C
+
T
V
=
C
+
Tp
V
=
C
+
V
V
V




χ
 ∂T V
 ∂V T

donde hemos utilizado que:
β=
1  ∂p 


p  ∂T V
y
α = pβχ
3.3. Coeficiente Joule-Kelvin
Por último, vamos a reescribir el coeficiente Joule-Kelvin:



 → µ JK =
 ∂H 

dH = nc p dT + 
 dp 
∂
p

T 
 ∂T 

 ∂p  H
µ JK = 
 ∂H 
 ∂V 
T
−
 −V

 ∂T  p
 ∂p T
=
nc p
nc p
Por Sergio Diez Berart