Examen _PDS_PSAJunio04_v2 - OCW UPM

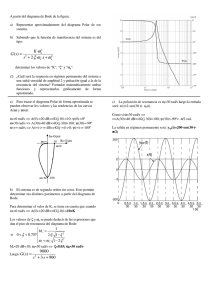
EXAMEN DE PROCESADO DIGITAL DE LA SEÑAL
EXAMEN DE PROCESADO DE LA SEÑAL AUDIOVISUAL
Universidad Politécnica de Madrid. E.U.I.T. Telecomunicación
Departamento de Ingeniería Audiovisual y Comunicaciones
11 de Junio de 2004, Plan 2000, Sonido e Imagen
1. Una señal x(t) cuyo espectro se muestra en la figura 1 se procesa con el diagrama de
bloques que aparece en la figura 2. Dibuje los espectros de todas las señales xi (n) e y(t).
Si la frecuencia de muestreo del convertidor C/D es de 24 kHz y la señal de entrada x(t)
es una sinusoide de 1 kHz, ¿qué señal se obtendría en la salida y(t)?
X(Ω)
π/(2T)
-π/(2T)
-π/T
Ω (rad/sg)
π/T
Figura 1. Espectro de la señal x(t)
x1 (n)
x(t)
C/D
x2 (n)
↓2
x3 (n)
↑3
FPBanda
x4 (n)
π/3 -- 2π/ 3
(ideal)
x5 (n)
↓3
x6 (n)
↑2
y(t)
D/C
T/4
T
Figura 2. Diagrama de bloques del sistema discreto
2. El diagrama de polos y ceros de un sistema discreto h(n) de coeficientes reales se
presenta en la figura siguiente de forma incompleta. Se pide:
• Complete el diagrama de polos y ceros
• Expresión H(z)
• Respuesta al impulso h(n)
• Ecuación en diferencias del sistema
• Dibujar de forma aproximada la respuesta en frecuencia (módulo) del sistema
orden 4
-3π/4
3. Sea hc(t) la respuesta al impulso de un filtro continuo LTI y hd[n] la respuesta al
impulso de un filtro en tiempo discreto LTI.
a) Si
e − at , t ≥ 0
hc (t ) = 
t<0
0,
siendo “a” una constante real positiva, determine la respuesta en frecuencia del
filtro en tiempo continuo y esboze su módulo.
b) Si hd [n] = T hc(nT), determine la respuesta en frecuencia del filtro discreto y
esboze su módulo.
c) Dado un valor de “a”, determine, en función de T, el mínimo valor del
módulo de la respuesta en frecuencia del filtro en tiempo discreto
4. Se desea diseñar un filtro FIR de fase lineal paso alto, con ωs=0.35π y ωp =0.5π,
atenuación mínima de 25 dB en la banda atenuada. Determine:
a) Respuesta impulsiva del filtro, y valor de la muestra h[5]
b) Proponga, dibuje y explique una estructura de cálculo para este filtro
c) Determine el porcentaje de ocupación de un sistema de procesado digital
basado en DSP que realiza este filtrado en tiempo real, sabiendo que el 10%
de los recursos del sistema se dedican a operaciones de entrada y salida, y
que el sistema es capaz de realizar 100Mops, con frecuencia de muestreo de
48.000 Hz.
5. Deseamos representar mediante FFT (N=2b ) la información espectral instantánea
de una señal de voz (fs=8kHz) analizando en ventanas consecutivas (sin solape) de
30 mseg. Describa:
a) Procedimiento a seguir para realizar el análisis y resolución espectral
obtenida
b) ¿Dónde encontramos la información correspondiente a 2kHz?
c) Si queremos analizar en detalle la información por debajo de 400Hz,
determine el procedimiento para realizar todo nuestro análisis espectral en
ese margen de frecuencias, indicando la nueva resolución espectral.
SOLUCIONES
1. Una señal x(t) cuyo espectro se muestra en la figura 1 se procesa con el diagrama de
bloques que aparece en la figura 2. Dibuje los espectros de todas las señales xi (n) e y(t).
Si la frecuencia de muestreo del convertidor C/D es de 24 kHz y la señal de entrada x(t)
es una sinusoide de 1 kHz, ¿qué señal se obtendría en la salida y(t)?
X(Ω)
π/(2T)
-π/(2T)
-π/T
Ω (rad/sg)
π/T
Figura 1. Espectro de la señal x(t)
x1 (n)
x(t)
C/D
x2 (n)
↓2
x3 (n)
↑3
x4 (n)
FPBanda
x5 (n)
↓3
π/3 -- 2π/ 3
(ideal)
x6 (n)
↑2
y(t)
D/C
T/4
T
Figura 2. Diagrama de bloques del sistema discreto
X1 (eiω)
1/T
-π/2
-π
-ω0
ω0
π/2
ω (rad)
π
X2 (eiω)
1/(2T)
-π/2 -2ω 0
-π
2ω0 π/2
ω (rad)
π
X3 (eiω)
1/(2T)
-π
-2π/3
-π/3
π/3
2π/3
π
ω (rad)
X4 (eiω)
1/(2T)
-π
-2π/3
π/3
-π/3
2π/3
ω (rad)
π
X5 (eiω)
1/(6T)
-π
-π/2 -2ω 0
2ω0 π/2
ω (rad)
π
X6 (eiω)
1/(6T)
-π
-π/2
-ω0 ω 0
π/2
ω (rad)
π
Y(Ω)
1/24
Ω (rad/sg)
-4π/T
-2π/T
4ω0 /T
2π/T
4π/T
b) Aparecen dos sinusoides ponderadas en amplitud por un factor 1/24.
Las frecuencias de las sinusoides son 4 kHz y 44 kHz.
2. El diagrama de polos y ceros de un sistema discreto h(n) de coeficientes reales se
presenta en la figura siguiente de forma incompleta. Se pide:
• Complete el diagrama de polos y ceros
• Expresión H(z)
• Respuesta al impulso h(n)
• Ecuación en diferencias del sistema
• Dibujar de forma aproximada la respuesta en frecuencia (módulo) del sistema
orden 4
-3π/4
Solución:
•
rc2=1
ωc2=3π/4
rc1=1
ωc1=π/4
orden 4
-3π/4
•
(
)(
) (
)(
)
H ( z ) = 1 − 2rc1 cosω c1 z −1 + z −2 1 − 2rc 2 cosωc 2 z −1 + z −2 = 1− 2cos(π / 4) z − 1 + z −2 1 − 2 cos(3π / 4) z −1 + z −2 =
(
)(
)
= 1 − 2 z −1 + z −2 1 + 2z −1 + z −2 = 1 + z − 4
•
h(n) = δ(n) + δ(n-4)
•
y(n) = x(n) + x(n-4)
|H(eiω)|
-π -3π/4
-π/4
-π/4
-3π/4
π
ω (rad)