to get the file - OCW UPM - Universidad Politécnica de Madrid

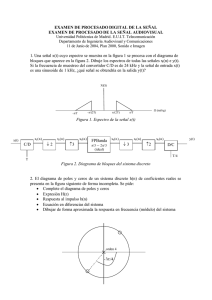
EXAMEN DE TRATAMIENTO DIGITAL DE LA SEÑAL
Universidad Politécnica de Madrid. E.U.I.T. Telecomunicación
Departamento de Ingeniería Audiovisual y Comunicaciones
11 de Junio de 2004, Plan 2000, Sistemas Electrónicos
1. Una señal x(t) cuyo espectro se muestra en la figura 1 se procesa con el diagrama de bloques
que aparece en la figura 2. Dibuje los espectros de todas las señales xi (n) e y(t). Si la frecuencia
de muestreo del convertidor C/D es de 16 kHz y la señal de entrada x(t) es una sinusoide de 2
kHz, ¿qué señal se obtendría en la salida y(t)?
X(Ω)
-π/T
π/(2T)
-π/(2T)
Ω (rad/sg)
π/T
Figura 1. Espectro de la señal x(t)
x1 (n)
x(t)
C/D
↓2
x2 (n)
↑3
x3 (n)
FPAlto
x4 (n)
2π/3
(ideal)
↓3
x5 (n)
↑2
x6 (n)
y(t)
D/C
T/3
T
Figura 2. Diagrama de bloques del sistema discreto
2. Se desea diseñar un filtro ranura a la frecuencia de p/4 radianes, con 2 polos y 2 ceros, y un
factor de calidad de 5. Calcular:
a) La posición de dichos ceros y polos en el plano Z.
b) La respuesta en frecuencia del filtro.
c) La ecuación en diferencias.
d) La estructura del filtro en la forma directa.
e) La frecuencia de muestreo para cancelar la frecuencia de 1 kHz.
3. a) Diseñar un filtro FIR paso banda de fase lineal mediante la técnica de ventanas, para una
frecuencia de muestreo de 4 kHz. Las especificaciones del filtro son: la primera banda de
transición va de 1 kHz a 1’2 kHz, y la segunda, de 5 kHz a 6 kHz; la atenuación ha de ser de al
menos 50 dB. b) Determinar la ecuación en diferencias y la transformada H(z) del filtro.
c) Representar el grafo de la estructura de cálculo. Datos:
Ventana
? ? (rad)
Atenuación (dB)
Rectangular
4p/(M+1)
21
Bartlett
8p/M
25
Hanning
8p/M
44
Hamming
8p/M
53
Blackman
12p/M
74
4. Una DSP es capaz de filtrar una señal, muestreada a 4 kHz, mediante la técnica overlap save,
a una velocidad máxima de 10 ventanas/s de 512 puntos. Calcular:
a) La longitud máxima que puede tener la respuesta al impulso de dicho filtro.
b) El grado de solapamiento máximo entre ventanas.
c) El número de productos y sumas reales efectuados por segundo. Datos: el número de
productos complejos efectuados en una DFT de N puntos es (N/2)log2 N; y el número de sumas
complejas Nlog2 N.
d) Repetir el apartado anterior en el caso de efectuar el filtrado mediante convolución lineal.
SOLUCIONES
1. Una señal x(t) cuyo espectro se muestra en la figura 1 se procesa con el diagrama de bloques
que aparece en la figura 2. Dibuje los espectros de todas las señales xi (n) e y(t). Si la frecuencia
de muestreo del convertidor C/D es de 16 kHz y la señal de entrada x(t) es una sinusoide de 2
kHz, ¿qué señal se obtendría en la salida y(t)?
X(Ω)
π/(2T)
-π/(2T)
-π/T
Ω (rad/sg)
π/T
Figura 1. Espectro de la señal x(t)
x1 (n)
x(t)
C/D
↓2
x2 (n)
↑3
x3 (n)
x4 (n)
FPAlto
↓3
2π/3
(ideal)
x5 (n)
↑2
x6 (n)
y(t)
D/C
T/3
T
Figura 2. Diagrama de bloques del sistema discreto
X1 (eiω)
1/T
-π/2
-π
-ω0
ω0
π/2
ω (rad)
π
X2 (eiω)
1/(2T)
2ω0 π/2
-π/2 -2ω 0
-π
ω (rad)
π
X3 (eiω)
1/(2T)
-π
-2π/3
π/3
-π/3
ω (rad)
π
2π/3
X4 (eiω)
1/(2T)
-π
-2π/3
-π/3
π/3
2π/3
π
ω (rad)
X5 (eiω)
1/(6T)
-π
-π/2 -2ω 0
2ω0 π/2
ω (rad)
π
X6 (eiω)
1/(6T)
-π
-π/2
-ω0 ω 0
π/2
ω (rad)
π
Y(Ω)
1/18
Ω (rad/sg)
-3π/T
-3π/2T
3ω0 /T
3π/2T
3π/T
b) Aparecen dos sinusoides ponderadas en amplitud por un factor 1/18.
Las frecuencias de las sinusoides son 6 kHz y 18 kHz.