La viga de la figura posee sección simétrica y en forma de “T” con

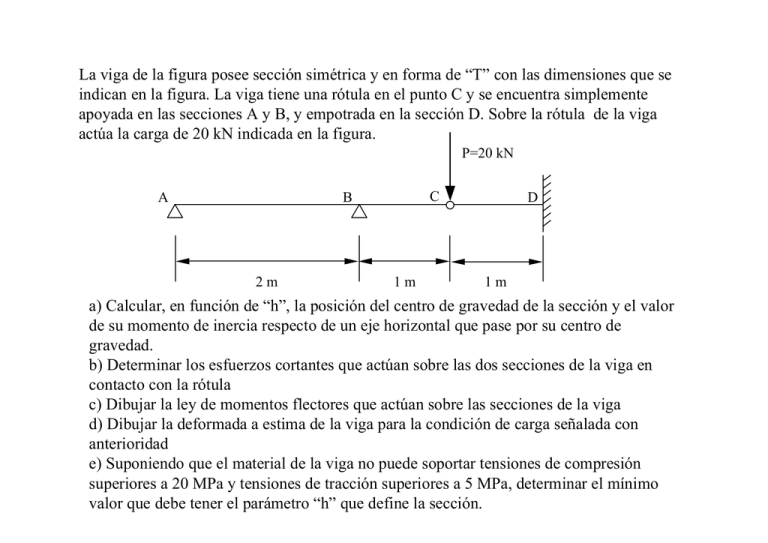
La viga de la figura posee sección simétrica y en forma de “T” con las dimensiones que se
indican en la figura. La viga tiene una rótula en el punto C y se encuentra simplemente
apoyada en las secciones A y B, y empotrada en la sección D. Sobre la rótula de la viga
actúa la carga de 20 kN indicada en la figura.
P=20 kN
A
C
B
2m
1m
D
1m
a) Calcular, en función de “h”, la posición del centro de gravedad de la sección y el valor
de su momento de inercia respecto de un eje horizontal que pase por su centro de
gravedad.
b) Determinar los esfuerzos cortantes que actúan sobre las dos secciones de la viga en
contacto con la rótula
c) Dibujar la ley de momentos flectores que actúan sobre las secciones de la viga
d) Dibujar la deformada a estima de la viga para la condición de carga señalada con
anterioridad
e) Suponiendo que el material de la viga no puede soportar tensiones de compresión
superiores a 20 MPa y tensiones de tracción superiores a 5 MPa, determinar el mínimo
valor que debe tener el parámetro “h” que define la sección.
h
h
h
h
3
3
Posición centro gravedad de la sección
5 h
6
17 4
Ix =
⋅h
162
P=20 kN
A
C
B
2m
D
1m
1m
P
C1
B
A
Q1
Q2
Q1
2m
L=1 m
EQUILIBRIO EN LA RÓTULA:
C2
D
Q2
L=1 m
Q1 + Q2 = P
COMPATIBILIDAD DE MOVIMIENTOS: ↓ Vc1 =↓ Vc 2
P
C1
B
A
Q1
Q1
2m
Q2
C2
Q2
L=1 m
L=1 m
↓ VC 2
Q1
B
A
D
Q2 ⋅ L3
=
3⋅ E ⋅ I
Q1.L
2L = 2 m
(
Q1 L ) ⋅ 2 L
θB =
3EI
↓ VC1
2 ⋅ Q1 ⋅ L3 Q1 ⋅ L3 Q1 ⋅ L3
=
+
=
3⋅ E ⋅ I
3⋅ E ⋅ I
E⋅I
Q1 = 5 kN
Q2 = 15 kN
R A = −2,5 kN (hacia arriba )
RB = 7,5 kN (hacia arriba )
RD = 15 kN (hacia arriba )
M D = 15 kN ⋅ m ( sentido horario)
15 kN·m
5 kN·m
A
B
C
D
15 kN·m
5 kN·m
A
A
B
B
C
C
D
D
La sección de máximo momento es la D en la que el momento es 15 kN.m en sentido
horario. La distribución de tensiones normales causada por un momento flector es:
M⋅y
σ =
Ix
Condición de máxima tracción:
En la fibra superior de la sección,
y = y max =
h
2
σ < σ t = 5 MPa
h > 242 ,68 mm
En la fibra inferior
5
y = y min = − ⋅ h
6
⇒ σ < σ c = 20 MPa ⇒ h > 181,26 mm
h = 242,68 mm