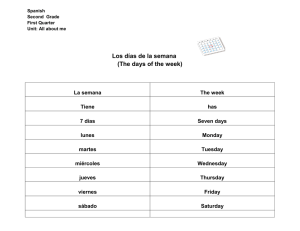
Outline What is a Model?

11/27/2007
Colorado River Delta (RCN-CRD) Meeting, Nov 14-16, 2007
Hydrogeologic Models:
fundamentals and
applications
Outline
What is a Model? Why to Model?
“
Principles and concepts of groundwater modeling
“
Conceptual models
“
General data requirements
“
Classifyy groundwater
g
models
“
Boundaries and model grid design
“
Execution, model calibration, and verification
“
Applications:
by
“
Mexicali Valley groundwater modeling
Jorge Ramírez-Hernández
“
Demonstration Site groundwater modeling
Instituto de Ingeniería, Universidad Autónoma de Baja California
What is a Model?
“
A model is any device that represents an
approximation of a field situation.
Analog Models.
Viscous fluid
models and
Electrical models
Physical Models. Laboratory sand tanks
Demonstrative tank of Instituto Mexicano de Tecnología del Agua, 2006
Modified from Custodio and Llamas, 1983
1
11/27/2007
What is a Model?
Mathematical Models. Simulate groundwater flow indirectly by
means of a governing equation.
∂
∂h
∂
∂h
∂
∂h
∂h
( K xx ) + ( K yy ) + ( K zz ) - W = S s
∂x
∂x
∂y
∂y
∂z
∂z
∂t
Solution:
Analytical. Very simple geometries and homogeneous porous
medium.
Numerical: help to solve much more complex models that are
easier to apply.
Why to use models?
Opinions about models
Disadvantages
• Models require too many data and therefore are too expensive to
assemble and run.
• They can never be proved to be correct and suffer from a lack of
scientific certainty.
• They are toys which provide intellectual stimulation.
Advantages
• Models are essential in performing complex analyses and in
making informed predictions.
• They allow more effective use of available data.
• One of the most valuable and practical tools.
• Models are often the best available alternative for analyzing
complex water resource problems.
Establishing the purpose of
modeling (first step)
Prediction
• Most groundwater modeling efforts are aimed to predict the
consequences of a proposed action.
Example: All american canal lining
Interpretation
• Models can be used in an interpretative sense to gain insight into
the controlling parameters in a site-specific setting or as a
framework for assembling and organizing field data and
formulating ideas about system dynamics.
Example: Mexicali valley groundwater dynamic
Generic
• Models be used to study processes in generic geologic settings.
Example: lake-groundwater interaction.
My goal is prediction, system
interpretation, or a generic modeling
exercise?
What do I want to learn from the model?
What question do I want the model to
answer?
Is a modeling exercise the best way to
answer the question(s)?
2
11/27/2007
Modeling
Protocol
Conceptual model
A conceptual model is a pictoral
representation of the groundwater
flow system.
purpose
p
of conceptual
p
model is to
The p
simplify as much as possible yet retains
enough complexity so that it adequately
reproduce system behavoir.
Block diagram
Cross section
Taken from Anderson and Woessner, 1992
Conceptual model
Steps for building a Conceptual model
Conceptual
model
(examples)
• Define the area of interest, i.e. identify
boundaries of the model.
model
• Define hydrostratigraphic units
• Prepare a water budget
• Define the flow system
Taken from Anderson and Woessner, 1992
3
11/27/2007
Conceptual model (examples)
3
2
Conceptual model
(examples)
April
2006
Abril
2006
16
RC-M12
PERFIL 2
RC-M10
RC
M10
14
HeightAltura
(m) (m)
Section 2.
RC-M9
RC-M11
12
10.095
10
8
Flujo
Subter
6
0
500
10.82
10.066
9.858
Río
ráneo
1000
1500
2000
Distance
(m)
Distancia (km)
Taken from Ramírez-Hernández, 1996
General data requirements
Physical framework
•
•
•
•
•
Geologic map and cross sections showing areal and vertical extents of boundaries
of the system.
Topographic map showing surface water bodies and divides.
Contour maps of elevation of the base of the aquifer and any bed.
Isopach maps of thickness of aquifer and confining beds.
Maps of the extent and thickness of stream and lake sediments.
Hydrogeologic framework
• Water table and piezometric maps.
• Hydrographs of groundwater head and surface water levels and discharge rates.
• Maps and cross sections of hydraulic conductivity distribution.
• Maps and cross sections of storage properties of aquifer.
• Hydraulic conductivity values and their distribution on stream and lake sediments.
• Spatial and temporal distribution rates of evapotranspiration, groundwater
recharge, surface-groundwater interaction, groundwater pumping, and natural
groundwater discharge.
Colorado River demonstration Site
Taken from Pérez et al, 2006
Classify groundwater flow models
By time dependency
• Steady state. The flow will be independent of time.
• Transient. The flow change with time.
By aquifer type:
• Confined.
• Unconfined (free).
Spatial dimension:
• Two-dimensional areal. Flow in W-E and N-S directions.
• Two-dimensional profile. Flow in horizontal and vertical directions.
• Full three dimensional. Flow in W-E, N-S and Z directions.
Other governing equations:
• Advective transport, unsaturated flow, inmiscible flow, density
effects, dispersion, flow through fractures, two-phases flow, etc.
4
11/27/2007
Ground-Water Flow equation
∂
∂h
∂
∂h
∂
∂h
∂h
( K xx ) + ( K yy ) + ( K zz ) - W = S s
∂x
∂x
∂y
∂y
∂z
∂z
∂t
Where:
Kxx, Kyy and Kzz Hydraulic conductivity along the x, y,
and z coordinate axes (L/T)
h
Potentiometric head (L)
W
Sources and sinks of water (T-1)
Ss
Specific storage (L-1)
t
time (T)
Time dependency
∂
∂h
∂
∂h
∂
∂h
∂h
( K xx ) + ( K yy ) + ( K zz ) - W = S s
∂x
∂x
∂y
∂y
∂z
∂z
∂t
Transient flow…
Ss
∂h
≠0
∂t
Stationary flow…
This equation, when combined with boundary and initial conditions, describes transient
three-dimensional ground-water flow in a heterogeneous and anisotropic medium.
Two-dimensional areal.
Ss
∂h
=0
∂t
Two-dimensional areal.
0
∂h
∂
∂h
∂
∂h
∂
∂h
( K xx ) + ( K yy ) + ( K zz ) - W = S s
∂x
∂x
∂y
∂y
∂z
∂z
∂t
∂
∂h
∂
∂h
∂h
( K xx ) + ( K yy ) - W = S s
∂x
∂x
∂y
∂y
∂t
If there is no changes of potentiometric head along z direction
∂
∂h
( K zz ) = 0
∂z
∂z
then
∂
∂h
∂
∂h
∂h
( K xx ) + ( K yy ) - W = S s
∂x
∂x
∂y
∂y
∂t
5
11/27/2007
Two-dimensional profile.
0
Two-dimensional profile (Cerro
Prieto geothermal field area)
∂
∂h
∂
∂h
∂
∂h
∂h
( K xx ) + ( K yy ) + ( K zz ) - W = S s
∂x
∂x
∂y
∂y
∂z
∂z
∂t
If there are no changes of potentiometric head along the Y direction
∂
∂h
( K yy ) = 0
∂y
∂y
then
Full three
dimensional.
∂
∂h
∂
∂h
∂
∂h
∂h
( K xx ) + ( K yy ) + ( K zz ) - W = S s
∂x
∂x
∂y
∂y
∂z
∂z
∂t
∂h
∂
∂h
∂
∂h
( K xx ) + ( K zz ) - W = S s
∂x
∂x
∂z
∂z
∂t
Type of Boundaries
Fixed Head
• Head is known
Constant Flow
• Flow is known
Head-dependent flow
• A combination of both
6
11/27/2007
Grid Design (orientation)
Grid Types
Finite differences
• Block centered grid
• Mesh centered grid
Finite Element
• Triangles
• Quadrilaterals
Grid Design (irregular)
Data to grid
(type of cell)
•Type of cell
•Active
•Inactive
•Injection
•Dimensions (x,y,z)
•Hydraulic Conductivity
•Storage Coef.
•Well, river, drain cells
•PET of upper cells
7
11/27/2007
Model Execution and Calibration
process
Potentiometric
maps
Initial solution.
• Because is a iterative solution process it is necessarily
to establish a initial value of h (potentiometric head).
Execution
• After all data has been translated to computer file the
model can be execute the model.
• Potentiometric maps is obtained.
Potentiometric
maps (example)
Flow model calibration
• Demonstrate that the model is capable of reproducing
field-measured heads and flows which are the
calibration values
• Is accomplished by findings a set of parameters,
boundary conditions and stresses that produce
simulated head and fluxes that MATCH FIELD
MEASURED VALUES within a preestablished
range of error
• Trial and error
• By solving the inverse problem
8
11/27/2007
Applications: Mexicali Valley aquifer
Wells location
Río
Drenes
Canales
Canal All American
Ciudad
Poblado
Contorno
Topográfico
Pilot Knob
Frontera
internacional
Drop 4
MEXI
LI
CA
NA
DE
DREN
L
DR
EN
CA
IND
EP
SA
LA ME
EN
DE
NCI
A
DR
EN
A
LT
DE
CA
R
L
NA
NORTE
REFORMA
RO
CA
RR
IL
LT
DE
A
N
IO
TE
C
O
O
LU
AL
IM
.
DREN
AYALA
DE
GA
TE
DR
EN
OR
Poblado
Río
STA.
L
NA
CA
CANA
L
C
PLAN
LE
CO
Ciudad
CLARA
CA
NA
L
CIP
IN
PR
SU
R
EL
R
TO
R
478
6
R
BA
EV
D
AL
DREN
20+6
00
DEL
SUR
SU
R
CANA
L
GU
ER
RE
RO
O.
NV
R
DREN
D
CO
ILC
CA
NA
L
FE
R
CTO
Contorno
Topográfico
Frontera
DREN
I
CH
XO
COLE
M
Internacional
Pozos CFE
Pozos agrícolas
Pozos para estudio
Taken from Díaz et al, 2000
Grid
Taken from Díaz et al, 2000
Hydraulic conductivity map
K = 90 m/día
K = 105 m/día
Ciudad
K = 115 m/día
Poblado
K = 125 m/día
Contorno
Topográfico
K = 128 m/día
Frontera Internacional
K = 500 m/día
K = 300 m/día
Río
Pozos agrícolas
K = 600 m/día
K = 1300 m/día
K = 10000 m/día
Canal All American
Contorno
Topográfico
Frontera Internacional
Río
Canal All American
Taken from Díaz et al, 2000
Taken from Díaz et al, 2000
9
11/27/2007
Stationary solution
Cells type
30
30
25
-5
20
25
10
0
5
15
20
15
5
20
10
Río
15
Ciudad
10
Contorno
Topográfico
Canal All American
Frontera Internacional
5
10
Canal Todo Americano (GHB)
Ríos Nuevo y Hardy (Drenes)
Ciudad
Río Colorado (Río)
Poblado
Contorno
Topográfico
Golfo de California (Pot. constante)
S. Cucapa, M. Gila, M. Chocolate (Impermeables)
Flujo de Arizona, San Luis Río Colorado (Recarga)
Frontera Internacional
Drenes y Canales en zona agrícola (Recarga)
10
5
Río
Canal All American
Configuración Piezométrica 1972 (CNA, 1972)
Configuración Piezométrica 1972 Modflow
Taken from Díaz et al, 2000
Taken from Díaz et al, 2000
Mexicali valley aquifer
Transient solution
R
Río
C
olo
ra
do
N
ue
vo
ío
Río
Ciudad
Ha
rd
y
Poblado
Contorno
Topográfico
Frontera Internacional
Río
Canal All American
Configuración Piezométrica 1994 (campo, 1994)
Configuración Piezométrica 1994 Modflow
Taken from Díaz et al, 2000
Taken from Blair et al, 2006
10
11/27/2007
Demonstrative site
Grid and river cells
60
160
150
50
140
130
40
120
110
30
100
90
80
20
70
60
10
50
40
30
20
10
L
K
Grosor de la capa
de baja
permeabilidad
CONDUCTANCIA DE RÍO = KLW/M
Taken from Pérez et al, 2006
1-J.MA.RGZ
Data to grid (Hydraulic conductivity)
G-3-1
136-B
8-BORQUEZ
11-VHER
7-3I II2 AL AMO-1
P-6-3
P-6-2
7-3 III7
4-L.C.
14-5
2-TREVINO
14-6
9-4-I3I
8 -L.CARD.
7-5-4
P-14 -7
3-OCKERSON
M-3-6
G-1-10
362-B
9-4-7
15-II-3
2 0-4-3
1 9000
19 000-I-C1 -5-4
1 -5-1
18-9-4I
G-3 -5
G-3-3
15-I-3
G-1-19
R-81 R-33
3-8-2B
4-H
9-8-2DE
1 45-B
32-0-2
R-13 9 6-9-2
1-H
52-CH
54-CH
53-CH
2-S. LUIS
3-H-B
9-M OCT
3-B
S-11
S-12
S-10
BCP-14
S-5
S-13
S-6
S-2
S-8
S-3
S-16
II-20
S-20
S-26
II-17
S-24 S-22 I I-19
29-CH
9-B
3 7-CH
13-VALLE
16-VALL
18-VALLE
3 6-CH
9-CH
12-CH
II-12
2-MEJOR
V-2-W
V-1
V-2
V-3
29 -VALLE
23-VALLE
15-CH
22-CH
17-CH
II-15B
II -18B II-16 II-14
V-5-W
V-4-W
39-CH
1 2-MOCT
G-1-17
G-3-14
3 -MOCT
37-4-3
46-CH
42-CH
49-CH
II-6
II-4II-5B II-7
II-9 II-8B
II-13
II-10
II-11
3-LESSER
1-BORDO
1-M ONUM
6-S.L UIS
37-4-1
8-CH
II -2
G-1-11
R-58
2 -HGO
A-N-4-5
5 7-CH
II-1
G-1-7
W
Ancho de río
Data to grid (Hydraulic conductivity)
G-3-13 1-ULLOA
G-3-6
1-OCKERSON
G-3-9
15-ORIB
1-ESQUER G-3-10 G-3-12
1 BORQUEZ
R-7
6-MERIDA
2-CUERVOS
R-107 7-BVHER
7-MORELOS
6-REP.MEX.
9-BORQUEZ
G-3 -2
G-1 -16
G-1 -15
G-1-21
G-1-6
G-1-4
M
Conductividad
Hidráulica del
material del lec
del río
V-4
V-5
V-9
V-10
V-11
V-12
19-CH
G-4-4
G-2-2
1-ESPER
5-B-COAH
22-VALLE
G-4-18
272-B
7
1
7
1
2
1
1
7
0
2
3
4
6
G-4 -15
27-VALLE
4-COAH
6-N.LEON
G-4 -3
7
5
8
9
0
1
1
1
2
4
1
3
1
1
5
1
6
1
7
1
1
9
8
1
1
2
2
0
2
3
2
5
2
7
2
8
2
4
2
6
2
9
2
0
3
2
3
1
3
3
5
4
3
6
3
8
3
0
4
3
4
2
4
7
3
9
3
1
4
4
6
4
9
4
1
5
3
5
6
7
7
7
1
8
8
2
9
9
5
0
1
1
9
0
1
1
9
1
2
1
0
3
1
9
6
1
6
1
8
6
1
6
1
6
1
3
6
7
5
6
1
6
4
6
1
2
6
1
0
6
1
1
5
1
8
7
4
5
1
1
5
9
6
5
1
5
1
5
1
3
1
3
5
1
2
5
1
0
5
1
4
1
8
4
1
7
1
4
4
1
9
1
4
6
1
5
4
3
4
1
4
1
2
4
1
1
3
1
4
1
0
8
3
1
3
61
2
3
1
3
1
3
1
3
1
4
2
1
6
2
1
8
2
1
2
7
4
2
1
1
2
0
2
1
2
1
1
5
1
1
4
1
1
7
6
1
1
0
1
1
2
0
7
0
1
0
1
3
0
1
2
0
0
9
4
9
3
9
9
7
6
9
1
9
0
9
9
8
5
8
8
8
7
6
3
8
2
8
0
8
8
7
7
5
7
3
2
1
7
0
8
6
7
6
5
6
4
6
3
6
2
6
1
6
0
6
9
5
8
5
6
5
5
8
4
5
4
1-BOLSA
7
4
0
5
2
5
4
5
7
5
9
6
4
7
6
7
9
7
4
8
5
8
4
0
1
6
0
1
0
8
3
8
1
3
5
9
2
1
3
5
7
9
3
2-N.MICH
1-N.MICH
3-N.MICH
G-4 -10
Díaz (2001)
S-5
II-13
II-10
S-13
S-6
II-11
S-2
S-8
S-3
S-16
II-20
II-12
S-20
II-17
S-26
II-15B
S-24 S-22
II-19
9-CH
18-VALLE
12-CH
29-VAL
23-VALLE
15-CH
22-CH
17-CH
II-18B II-16 II-14
19-CH
G-4-4
1-ESPER
5-B-COAH
G-2-2
22-VALLE
G-4-18
272-B
27-VALLE
1.21E1.52E-08
06
4-COAH
6-N.LEON
G-4-3
1-BOLSA
2-N.MICH
Isocontornos referidos al nivel del mar (1m).
1-N.MICH
3-N.MICH
Taken from Pérez et al, 2006
11
11/27/2007
Stationary solution
Thanks
8.7
1 2 34 8.4
9.7
9
6
81
8.1
13
7
26
5.5
27
21
22
23 7
24
1
8
7.6
7
18
19
10
10 11
12 10.7
5
9.4
7
8
8.2
14
15
16
8
7.6
20
25
7
6
Taken from Pérez et al, 2006
12