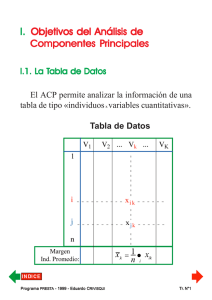
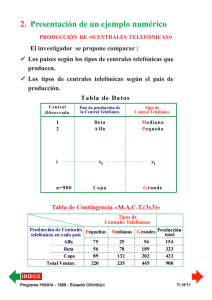
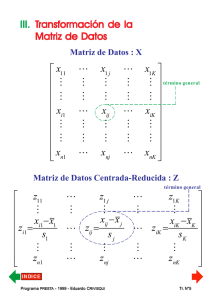
Los n

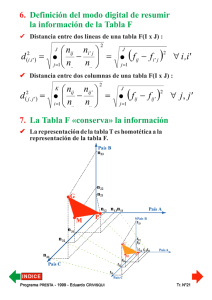
3. Representación conjunta de la inercia de
las nubes de puntos N(I) y N(J)
a) Justificación de la representación conjunta
✔ El origen de los dos espacios es el Centro de Gravedad de cada
nube de puntos;
✔ La inercia de las dos nubes de puntos es la misma;
✔ La suma de los valores propios asociados a cada matriz de
inercia es la misma;
I
Ν (I )
GL
=I
Ν (J )
GC
p
Ν (I )
α
= ∑λ
α =1
p
= ∑ λΝα( J ) = ϕ 2
α =1
✔ Se puede demostrar que los valores propios son los mismos y
del mismo orden;
λΝ1 ( I ) = λΝ1 ( J ) ; λΝ2 ( I ) = λΝ2 ( J ) ; ...; λΝp( I ) = λΝp( I )
➩
Esos espacios no son idénticos... pero son de la misma
«naturaleza».
➩
Se los puede superponer... porque existen fuertes relaciones
entre esos espacios.
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°72
b) Fórmulas de Transición
 1  J f ij
 ∑ Gα ( j )
Fα (i ) = 
 λ α  j=1 fi .
∀i ∈ I
 1  I f ij
Gα ( j ) = 
 ∑ Fα (i )
 λ α  i=1 f .j
∀j ∈ J
c) Significado de las Fórmulas de Transición
✔
La "lectura" de los planes factoriales depende del
significado de las fórmulas de transición.
✔
Las fórmulas de transición presentan un gran interés
práctico desde el punto de vista del cálculo...
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°73
4. Elementos suplementarios o ilustrativos
en un análisis
a) Empleo de elementos suplementarios
La técnica de «elementos suplementarios» es un instrumento metodológico adecuado para guiar y controlar un
razonamiento inductivo aplicado al objeto de estudio.
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°74
b) Coordenadas de los elementos suplementarios
Sea S un perfil suplementario en columna de J elementos :
f f
f
f1sJ 
S =  ; ; ...; ; ...; s 
f
f1. 
f f
s
11
s
1.
siendo :
s
1j
s
1.
s
12
s
1.
J
f = ∑ f1sj
s
1.
j =1
Ponemos en escala el perfil S :
 f11s
f1sj
f1sJ 
; ...; s
S=  s
; ...; s

f1. f . j
f 1. f . J 
 f1. f .1
Centrando el perfil S en GC :
 f11s
−
S=  s
 f1. f .1
f .1 ; ...;
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
f1sJ
s
1.
f
f .J
−

f .J 

Tr. N°75
Coordenadas del punto-perfil S (ponderado y centrado en
GC) por proyección sobre los ejes factoriales
 f1sj
−
Gα (S ) = ∑  s
f. j
j =1 f1.

J

f . j  ⋅ uα ( j )

f. j
siendo : uα ( j ) =
Gα ( j )
λα
s
f


1
1j
⇒ Gα (S ) =
∑
s − f . j  ⋅ Gα ( j )

λ α j =1  f1.

J
Fórmula muy semejante a las relaciones de transición.
c) Coeficientes de ayuda a la interpretación
de los elementos suplementarios
✔ El coeficiente de «contribución a la inercia de un factor» no
tiene sentido en el caso de un elemento suplementario, puesto
que son puntos de masa nula.
✔ Calidad de representación sobre el eje... (?)
✔ Valores test
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°76
5. Valores-test
Llamamos :
njq :
la cantidad de individuos que presentan la j-ésima modalidad de la partición en línea y que presentan la q-ésima
modalidad de la partición en columna.
n:
la cantidad de individuos observados.
nj. :
cardinal de la j-ésima modalidad de la partición en línea.
n.q :
cardinal de la q-ésima modalidad de la partición en
columna.
H0 : Los njq individuos han sido seleccionados al azar, sin
restitución, entre los n individuos observados, tirando una
muestra aleatoria de nj. individuos.
Hipótesis nula : µ = pq/j − p.q = 0
n jq
[podemos estimar: pq/j ≈ n j.
y
p.q ≈
n.q
n
].
H1 : Los njq individuos no han sido seleccionados al azar.
Hipótesis alternativa : µ ≠ pq/j − p.q ≠ 0
- si se seleccionan nj. individuos de un conjunto de n individuos,
de manera tal que todos tengan la misma probabilidad de ser
elegidos ( p = p.q ) ;
- si esa selección es hecha sin restitución (lo cual es el caso aquí
puesto que cada individuo recibe uno y sólo un atributo de cada
variable ) ;
- y si la observación de un individuo extraído aleatoriamente
consiste en verificar el hecho que éste posea o no la modalidad
q de la variable correspondiente...
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°77
La cantidad njq de individuos que poseen la q-ésima modalidad y que pertenecen a la j-ésima clase de la partición en línea,
es un valor que sigue una variable aleatoria ξ , que admite una
distribución de probabilidades hipergeométrica, especificada
por tres parámetros :
x ~ ξ (n, nj., p)
Si llamamos :
n jq
p=
n j.
n − n jq = n j.. (1 − p )
y
La media de la v.a. ξ : µ = n j. p
(
)
 n jq   n − n j. 


La varianza de la v.a. ξ : σ = n jq 1 −
 n j .   n − 1 


2
Probabilidad de observar njq ind. en la muestra de nj.:
( ( ))
PH0 = ξ n jq
Si njq es grande, la probabilidad hipergeométrica asociada a
ese valor es pequeña y la H0 es menos admisible.
Si n y nj. son suficientemente grandes, la v.a. ξ se ajusta a una
v.a. binomial : ψ ≈ B(n , p ), la cual converge sobre una v.a.
normal : ω ≈ N (µ ,σ ) . Centrando y reduciendo la v.a. ω ≈ N(µ , σ ),
definimos una v.a. normal reducida : ζ ≈ N (0,1).
La probabilidad asociada a la ocurrencia de un valor njq es
igual a la probabilidad que la ley normal N (0,1) sea superior o
igual al valor ujq calculado sobre la «media de la muestra» de los
nj. individuos de la modalidad que nos interesa.
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°78
el valor u jq =
p−µ
es llamado «Valor-Test».
σ
De modo que : u jq σ = p − µ
Si una modalidad de una variable nominal ilustrativa presenta un «valor-test» superior a 1.98 (inferior a -1.98) sobre un
eje α, se debe rechazar la H0 y conservar la H1.
Se concluye que esa modalidad está «bien representada»
α.
sobre ese eje α
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°79
6. Fórmula de reconstrucción de los datos
∀i∈I y ∀ j ∈J


1
fij = pi p j 1 + ∑ Fα (i )Gα ( j )
α λα


Desarrollando esta expresión para α = 1, 2, ...., p
siendo : f i. = pi y f.j = pj ...
➩ α = 0 ; f ij = pi p j
1 F (i )G ( j )
α
=
=
+
f
p
p
p
p
1
;
➩
ij
i j
i j
1
λ 1
1
1
➩ α = 2 ; f ij = pi p j + pi p j F1 (i )G1 ( j ) +
λ1
pi p j 1 F2 (i )G2 ( j )
λ2
1
➩ α = p ; f ij = pi p j + pi p j F1 (i )G1 ( j ) +
λ1
+ ... + pi p j
1
Fp (i )G p ( j )
λp
✔
Cada etapa constituye una aproximación sucesiva
de la tabla F.
✔
Cada una de esas etapas es una tabla de las mismas
dimensiones que F.
✔
La reconstrucción de F se hace por la suma de tablas
producto de márgenes (una dimensión), dadas por los
ejes factoriales sucesivos.
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°80
7. Esquema del proceso de transformación
de los datos
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°81