Anejo 1. Problemas - Ingeniería Mecánica Aplicada y Computacional

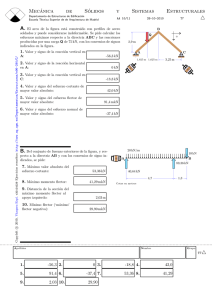
 2004 V. BADIOLA
DPTO. INGENIERÍA MECÁNICA, ENERGÉTICA Y DE MATERIALES
Anejo 1. Problemas
A1.1. PROBLEMAS TEMA 1:
PROBLEMA 1
Determinar sobre el elemento mecánico de la figura siguiente, la flecha en el punto A por el
método de Castigliano.
Considerar E=210Gpa y coeficiente de Poisson ν=0.3.
D
L
r
P
d
L
L/2
2L
Punto A
T
Datos:
L=300mm
d=40mm
D=44mm
r=2mm
P=T/L
P=1000N
- 147
DISEÑO DE MÁQUINAS I
 2004 V. BADIOLA
PROBLEMA 2
Determinar el ángulo en A debido a la
flexión:
a1=50mm
b1=150mm
a2=100mm
E=210Gpa
D=20mm
F1=45kgr
F2=140kgr
MT=3000cm·kgr
A1.2. PROBLEMAS TEMA 2:-
DISEÑO DE MÁQUINAS I
- 148 -
 2004 V. BADIOLA
DPTO. INGENIERÍA MECÁNICA, ENERGÉTICA Y DE MATERIALES
A1.3. PROBLEMAS TEMA 3:
PROBLEMA 1
Determinar el fallo de la pieza de la figura según el criterio de Mohr modificado.
Barra 2
Barra 1
T
z
DATOS:
Fa=1KN
Fb=2KN
T=3KN·m
L=1m
D=50mm
E=210GPa
Sut=700MPa
Suc=900MPa
x
y
Fa
Barra 1:
Fb
Por simetría, Iy=Iz
Además, Ix=Iy+Iz
E Ix es el momento polar de inercia Ip:
z
Tracción
π ⋅ D4
=I
32
Iy = Iz = I / 2
Ip =
Compresión
y
Barra 2:
z
Por simetría, Ix=Iz
Además, Iy=Ix+Iz
E Iy es el momento polar de inercia Ip:
π ⋅ D4
=I
32
Ix = Iz = I / 2
Ip =
x
- 149
DISEÑO DE MÁQUINAS I
 2004 V. BADIOLA
Barra 1:
T
Fa
Fb
My=Fb· L, flexión en plano XZ
Mz=Fa· L, flexión en plano XY
Mx=T, torsión
z
z
σx =
My ⋅ R
y
Iy
=
Fb ⋅ L ⋅ R
I/ 2
σx =
y
M z ⋅ R Fa ⋅ L ⋅ R
=
Iz
I/ 2
τ=
T ⋅R T ⋅R
=
Ip
I
Barra 2:
Mz=Fa· L
z
T
z
My=Fb· L
Fa
x
Fb
Mx=Fb· L, flexión en plano YZ
τ=
My=Fb· L, torsión
Fb ⋅ L ⋅ R
I
σy =
M x ⋅ R Fb ⋅ L ⋅ R
=
Ix
I/ 2
x
Mx=T, flexión en plano YZ
σy =
Mz=Fa· L, flexión en plano XY
z
Fa, axial
x
σy =
σy =
Fa
A
Mx ⋅ R T ⋅ R
=
Ix
I/ 2
M z ⋅ R Fa ⋅ L ⋅ R
=
Iz
I/ 2
Barra 1:
σx =
z
Punto A:
τ=
A
B
y
Punto B:
σx =
τ=
Fb ⋅ L ⋅ R
I/ 2
T ⋅R
I
Fa ⋅ L ⋅ R
I/ 2
τ
T ⋅R
I
σ
(σ, τ )
Barra 2:
z
Punto C,E:
C
σy =
τ=
D
x
σy =
E
DISEÑO DE MÁQUINAS I
Punto D:
τ=
Fb ⋅ L ⋅ R Fa T ⋅ R
+
−
I/ 2
A
I/ 2
Fb ⋅ L ⋅ R
I
σ1, σ 2 =
σ
±
2
σ
2
2
Fa Fa ⋅ L ⋅ R
+
A
I/ 2
Fb ⋅ L ⋅ R
I
- 150 -
+ τ2
 2004 V. BADIOLA
DPTO. INGENIERÍA MECÁNICA, ENERGÉTICA Y DE MATERIALES
Realmente puntos A, B, C y D puntos críticos?
Realmente, sobre una sección determinada, tenemos
Ejemplo, Barra 1:
Mz=Fb· x
Barra 2
z
My=Fa· x
Barra 1
T
y
Los momentos son vectores
Fa
M = M 2z + M 2y
Fb
tg α =
se pueden sumar vectorialmente
Mz
M
Mz
My
α
My
z
M ⋅R
σ=
=
I/ 2
(Fa ⋅ L )2 + (Fb ⋅ L )2 ⋅ R
I/ 2
τ=
=
(Fa )2 + (Fb )2 ⋅ L ⋅ R
M
α
y
I/ 2
T ⋅R
I
Cuando se tiene momentos de flexión perpendiculares que actúan sobre una sección, el
momento resultante se calcula como suma vectorial de los momentos actuantes.
Así, los valores de tensión que se deben emplear para calcular las tensiones principales serán
los correspondientes a los esfuerzos resultantes actuantes.
Sustituyendo valores tenemos:
Barra 1:
M⋅R
σ=
=
I/ 2
τ=
(Fa ⋅ L )2 + (Fb ⋅ L )2 ⋅ R
I/ 2
=
(Fa )2 + (Fb )2 ⋅ L ⋅ R
I/ 2
= 214.2MPa
T ⋅R
= 122.2MPa
I
σ 1,2 = 107.1 ± 162MPa
Barra 2:
F M⋅R
σ= a +
=
A
I/ 2
τ=
(Fa ⋅ L )2 + (Fb ⋅ L − T )2 ⋅ R
I/ 2
= 115.5MPa
Fa ⋅ L ⋅ R
= 81.5MPa
I
σ1,2 = 57.75 ± 100MPa
- 151
DISEÑO DE MÁQUINAS I
 2004 V. BADIOLA
A1.4. PROBLEMAS TEMA 4:
PROBLEMA 1
El eje de la figura está sometido a un momento flector alternativo. Está fabricado con acero de
resistencia a la rotura Su=1000Mpa y acabado por rectificado. Calcular momento flector Mf para una
vida de 200.000 ciclos:
suponer M=100mkg±Mf; Sy=800Mpa
además actúa una carga axial F=70±35KN
además un esfuerzo torsor compuesto por un par medio más un par alternado
MTm ± Mam = 100000Nmm ± 50000Nmm
R=1.5
30
33
Apartado a)
La pieza está sometida a flexión alternada. El diagrama S-N para flexión alternada es el mismo
que para flexión rotativa y es:
En primer lugar debemos calcular el límite de resistencia a fatiga del acero:
S e = K a ⋅ K b ⋅ K q ⋅ K d ⋅ K e ⋅ K g ⋅ K c ⋅ S 'e
Acero con Sut<1400Mpa, luego S'e = 0.5 ⋅ Sut = 500MPa .
Factores modificativos:
❐ Superficie Ka: K a = 1.58 ⋅ (1000 )−0.085 = 0.878
❐ Tamaño Kb: como es flexión alternada, se calcula el diámetro equivalente
−0.1133
de
de = 0.37 ⋅ d = 0.37 ⋅ 30 = 11.1mm . Y ahora el factor Kb: K b =
= 0.958 , con d en mm
7.62
❐ Carga Kq: en flexión alternada este factor vale 1.
DISEÑO DE MÁQUINAS I
- 152 -
 2004 V. BADIOLA
DPTO. INGENIERÍA MECÁNICA, ENERGÉTICA Y DE MATERIALES
❐ Concentración de tensiones: K e =
1
Kf
r = 1.5 = 0.05
d
30
→ GraficaA.26.14
D = 33 = 1.1
d
30
K t = 2.1
Análogamente se calcula se sensibilidad a la entalla q=0.88
Luego, K f = 1 + q ⋅ (K t − 1) = 1 + 0.88 ⋅ (2.1 − 1) = 1.968 El factor de concentración de tensiones
Kf’ a 103 ciclos es: K f = 1 + c ⋅ (K f − 1) siendo c =
'
0.3 ⋅ S u
− 0.1 = 0.328 . Luego K f ' = 1.318 .
700
❐ Efectos diversos Kg=1
❐ Factor de confiabilidad Kc: puesto que la resistencia Su=1000Mpa es una resistencia media y
por lo tanto se le asocia una confianza del 50%, calculamos este factor para una confianza del 90%.
K c = 1 − 0.08 ⋅ 1.3 = 0.896 .
A continuación, con todos los factores se calcula:
( )
S e 10 6 = K a ⋅ K b ⋅ K q ⋅ K d ⋅ K e ⋅ K g ⋅ K c ⋅ S 'e = 191.5MPa
Análogamente, la resistencia a 1000 ciclos se ve reducida por Kf’:
( )
S 103 =
0.9 ⋅ Sut
= 682.8MPa
Kf '
De esta forma queda definida la curva SN:
A 200.000 ciclos, la resistencia a la fatiga S se obtiene como:
log
0.9 ⋅ Sut
0.9 ⋅ Sut
− log(Se ) log
− log(S )
Kf '
Kf '
=
6−3
log( 200000 ) − 3
S = 257.7MPa
El criterio de Goodman establece que: σm S + σa S = 1
ut
e
cs
- 153
cs
DISEÑO DE MÁQUINAS I
 2004 V. BADIOLA
σa
Asumiendo cs=1, y puesto que el momento flector alternado produce tensión media nula,
Se
= 1 → σa = Se .
Se es la resistencia a fatiga a un número determinado de ciclos, en nuestro caso el criterio de
diseño es 200.000 ciclos luego Se=257.7Mpa.
La máxima tensión es:
σa,max =
σ a,max ⋅ π ⋅ d 3 257.7 ⋅ π ⋅ 30 3
Mf ⋅ d / 2
,
luego
M
=
=
= 683090Nmm
f
4
32
32
πd
64
Otra forma de trabajar es considerar la concentración de tensiones como concentrador de
tensiones y no reductor de resistencia. Entonces,
( )
S e 10 6 = K a ⋅ K b ⋅ K q ⋅ K d ⋅ K g ⋅ K c ⋅ S 'e = 376.8MPa
De esta forma queda definida la curva SN:
A 200.000 ciclos, la resistencia a la fatiga S se obtiene como:
log(0.9 ⋅ S ut ) − log(Se ) log(0.9 ⋅ S ut ) − log(S )
=
6−3
log(200000) − 3
El criterio de Goodman establece que:
σm
S ut
cs
S = 461MPa
+
σa
Se
cs
=1
Asumiendo cs=1, y puesto que el momento flector alternado produce tensión media nula,
σ a ⋅ Kf
S
= 1 → σa = e .
Se
Kf
La máxima tensión es:
σ a,max
σ a,max ⋅ π ⋅ d 3 234.5 ⋅ π ⋅ 30 3
Mf ⋅ d / 2
=
, luego M f =
=
= 621593Nmm
4
32
32
πd
64
Apartado b)
En este caso, el momento flector medio produce una tensión media:
DISEÑO DE MÁQUINAS I
- 154 -
 2004 V. BADIOLA
DPTO. INGENIERÍA MECÁNICA, ENERGÉTICA Y DE MATERIALES
σ m,max =
M m ⋅ d / 2 1000000 ⋅ 30 / 2
=
= 377MPa
4
4
πd
π 30
64
64
Podemos seguir cualquiera de las líneas de trabajo con el factor Kf (concentrador/reductor):
Si lo consideramos reductor de resistencia, tenemos que la resistencia a fatiga a 200.000 ciclos
era 257.7Mpa.
σm
S ut
+
σa
Luego: M f =
Se
= 1 → σa = Se ⋅ 1−
σ a ,max ⋅ π ⋅ d 3
32
=
σm
(
= 257.7 1 − 377
S ut
1000
) = 160.5MPa
160.5 ⋅ π ⋅ 30 3
= 425440Nmm
32
Si consideramos concentrador de tensión, asumiendo que se trata de un material dúctil:
σm
S ut
+
σ a ⋅ Kf
Luego: M f =
Se
= 1 → σa =
σ a ,max ⋅ π ⋅ d 3
32
=
Se ⋅ 1−
σm
S ut
Kf
=
(
461⋅ 1 − 377
1.968
)
1000 = 145.9MPa
145.9 ⋅ π ⋅ 30 3
= 386836Nmm
32
Es necesario por último comprobar la fluencia:
σ max = σ m + σ a = 377 + 160.5 = 537.5MPa < S y = 800MPa
Apartado c)
Además de los momentos flectores alternado y medio actúa un esfuerzo axial de 70KN±35KN.
En este caso, estamos en el caso 2) Esfuerzos combinados, una misma componente de tensión
(tensión axial σ x ), pero distintos factores modificativos.
Tenemos dos límites de fatiga, uno para cada tipo de esfuerzo:
σ mT = σ m,flector + σ m,axial
Existen dos formas de plantear este caso:
Primera forma:
Segunda forma:
σ mT σ a,flector σ a ,axial
+
+
=1
Su S N,flector S N,axial
S
σ mT σ a,flector + σ a,axial ⋅ α N
+
= 1 , donde α N = N,flector
Su
S N,flector
S N,axial
Calculamos el límite de fatiga para carga axial:
❐ Superficie Ka: K a = 1.58 ⋅ (1000 )−0.085 = 0.878
❐ Tamaño Kb (d>10mm): Kb=0.6
❐ Carga Kq: 0.923 (axial y Su<1520Mpa)
❐ Concentración de tensiones: K e =
- 155
1
Kf
DISEÑO DE MÁQUINAS I
 2004 V. BADIOLA
r = 1.5 = 0.05
d
30
→ GraficaA.26.13
33
D =
= 1.1
d
30
K t = 2.5
Análogamente se calcula se sensibilidad a la entalla q=0. 88
Luego, K f = 1 + q ⋅ (K t − 1) = 1 + 0.88 ⋅ (2.5 − 1) = 2.32 El factor de concentración de tensiones
0.3 ⋅ S u
'
− 0.1 = 0.328 . Luego K f = 1.4337 .
700
Kf’ a 103 ciclos es: K f = 1 + c ⋅ (K f − 1) siendo c =
'
❐ Efectos diversos Kg=1
❐ Factor de confiabilidad Kc: puesto que la resistencia Su=1000Mpa es una resistencia media y
por lo tanto se le asocia una confianza del 50%, calculamos este factor para una confianza del 90%.
K c = 1 − 0.08 ⋅ 1.3 = 0.896 .
Planteamos el problema con el factor de concentración como reductor de resistencia:
( )
S e 10 6 = K a ⋅ K b ⋅ K q ⋅ K d ⋅ K e ⋅ K g ⋅ K c ⋅ S 'e = 93.9MPa
A 1000 ciclos, el punto en lugar de ser 0.75Su es :
0.75 ⋅ S u 0.75 ⋅ 100
=
= 523.1MPa
Kf '
1.43375
Luego se obtiene a 200.000 ciclos:
log
0.75 ⋅ S ut
Kf '
− log(Se )
6−3
=
log
0.75 ⋅ S ut
Kf '
− log(S )
log(200000) − 3
S = 139.4MPa
Finalmente se aplica el criterio de Goodman de la segunda forma, teniendo en cuenta que:
S
σ
+ σa,axial ⋅ αN
257.7
σ
αN = N,flector =
= 1.85 . Luego: mT + a,flector
=1
Su
SN,flector
SN,axial
139.4
σ mT = σ m,flector + σ m,axial = 377 +
70000
= 476MPa
2
π ⋅ 30
4
σaT = σa,flector + σa,axial ⋅ α = σa ,flector +
35000
⋅ 1.85 = σa ,flector + 91.5MPa
2
π ⋅ 30
4
Y operando, se despeja la tensión alterna debida al flector alternado:
476 σa ,flector + 91.5
+
=1
1000
257.7
Luego: M f =
σa,flector = 43.5
σa ,max ⋅ π ⋅ d3 43.5 ⋅ π ⋅ 303
=
= 115561.8Nmm
32
32
A continuación se verifica la fluencia:
σmax = σm + σa,flector + σa,axial = 476 + 43.5 + 49.5 = 568MPa < S y = 800MPa
Apartado d)
DISEÑO DE MÁQUINAS I
- 156 -
DPTO. INGENIERÍA MECÁNICA, ENERGÉTICA Y DE MATERIALES
 2004 V. BADIOLA
En este caso, se supone que actúa además un esfuerzo torsor compuesto por un par medio más
un par alternado.
Calculamos el límite de fatiga para torsión:
❐ Superficie Ka: K a = 1.58 ⋅ (1000)
−0.085
❐ Tamaño Kb (d=30mm): K b =
30
7.62
= 0.878
−0.1133
= 0.856
❐ Carga Kq: 0.577 (torsión), pero luego no volveremos a multiplicarlo por 0.577 en la gráfica
siguiente:
❐ Concentración de tensiones: K e =
1
Kf
r = 1.5 = 0.05
d
30
→ GraficaA.26.15
D = 33 = 1.1
d
30
K t = 1.65
Análogamente se calcula se sensibilidad a la entalla q=0.97 (acero templado)
Luego, K f = 1 + q ⋅ (K t − 1) = 1.6305 El factor de concentración de tensiones Kf’ a 103 ciclos es:
K f = 1 + c ⋅ (K f − 1) siendo c =
'
0. 3 ⋅ S u
'
− 0.1 = 0.328 . Luego K f = 1.207 .
700
❐ Efectos diversos Kg=1
❐ Factor de confiabilidad Kc: puesto que la resistencia Su=1000Mpa es una resistencia media y
por lo tanto se le asocia una confianza del 50%, calculamos este factor para una confianza del 90%.
K c = 1 − 0.08 ⋅ 1.3 = 0.896 .
Planteamos el problema con el factor de concentración como reductor de resistencia:
( )
S e 10 6 = K a ⋅ K b ⋅ K q ⋅ K d ⋅ K e ⋅ K g ⋅ K c ⋅ S 'e = 118.8MPa
A 1000 ciclos:
0.72 ⋅ Su 0.72 ⋅ 1000
=
= 596.44MPa
Kf '
1.207
- 157
DISEÑO DE MÁQUINAS I
 2004 V. BADIOLA
Luego se obtiene a 200.000 ciclos:
0.72 ⋅ S ut
log
− log(Se )
Kf '
6−3
=
log(596.44 ) − log(S )
log(200000) − 3
S = 173MPa
El momento torsor produce una tensión de cortadura:
τm =
Tm ⋅ d / 2 16 ⋅ Tm
=
= 18.86MPa
π ⋅ d 4 / 32 π ⋅ d 3
La tensión media equivalente es la tensión media de Von-Mises:
σ eqm =
(σ
+ σ xm,axial ) + 3 ⋅ τ xym =
2
xm,flector
2
(377 + 99)2 + 3 ⋅ 18.86 2
= 477MPa
Se calculan los factores α tomando como referencia la resistencia a la fatiga a flexión:
Flexión: α1 = 1
Axial: α 2 =
SN,flexion
SN,axial
Torsión: α 3 =
=
257.7
= 1.85
139.4
SN,flexion
SN,torsionl ⋅ 3
=
257.7
= 0.86
173 ⋅ 3
La tensión alternada equivalente es la tensión de Von-Mises, incluyendo los factores:
(σ
σeqa =
+ σ xa,axial ⋅ α 2 ) + 3 ⋅ (τ xya ⋅ α 3 ) =
2
xa , flector
2
(σ
+ 49.51 ⋅ 1.85 ) + 3 ⋅ (9.43 ⋅ 0.86 )
2
xa , flector
2
Ya que:
τa =
Ta ⋅ d / 2 16 ⋅ Ta 16 ⋅ 50000
=
=
= 9.43MPa
π ⋅ d4 / 32
π ⋅ d3
π ⋅ 303
Se aplica ahora el criterio de Goodman:
σeq,m
Su
+
σeq,a
SN,flector
=1→
477 σeq,a
+
=1
1000 257.7
σ xa,flector = 42.47MPa
σa,max ⋅ π ⋅ d3 42.47 ⋅ π ⋅ 303
Luego: M f =
=
= 112597Nmm
32
32
Por último, se verifica la fluencia:
σeqmax =
(σ
+ σ xmas ,axial ) + 3 ⋅ τ xymax =
2
xmax , flector
2
((377 + 42.47) + (99 + 49.51))2 + 3 ⋅ (18.86 + 9.43)2
= 560MPa
Puesto que es menor que 800Mpa, se verifica que no ha entrado en fluencia.
DISEÑO DE MÁQUINAS I
- 158 -
 2004 V. BADIOLA
DPTO. INGENIERÍA MECÁNICA, ENERGÉTICA Y DE MATERIALES
PROBLEMA 2
El elemento de la figura está empotrado en un extremo y sometido a las cargas indicadas en su
extremo libre. Se desea determinar el valor de la carga alternada Pa que será capaz de soportar
durante 150.000ciclos.
Material: acero Su=1000Mpa, Sy=800Mpa
1000kg±2·Pa
400
500kg±·Pa
Φ=44
100
r=2
200
Φ=40
La sección crítica es la correspondiente a la entalla, puesto que posee el cambio de sección y
por lo tanto la concentración de tensiones.
En dicha sección tenemos flexión alternada y torsión. Corresponde al caso 3.
En primer lugar debemos calcular el límite de resistencia a fatiga del acero:
Límite de resistencia a la fatiga a flexión alternada:
S e = K a ⋅ K b ⋅ K q ⋅ K d ⋅ K e ⋅ K g ⋅ K c ⋅ S 'e
Acero con Sut<1400Mpa, luego S'e = 0.5 ⋅ Sut = 500MPa .
Factores modificativos:
❐ Superficie Ka: Asumimos
−0.265
K a = 4.51 ⋅ (1000)
= 0.7231
que
está
maquinado
o
estirado
en
frío:
❐ Tamaño Kb: como es flexión alternada, se calcula el diámetro equivalente
−0.1133
de
d e = 0.37 ⋅ d = 0.37 ⋅ 40 = 14.8mm . Y ahora el factor Kb: K b =
= 0.9275 , con d en mm
7.62
❐ Carga Kq: en flexión alternada este factor vale 1.
❐ Concentración de tensiones: K e =
- 159
1
Kf
DISEÑO DE MÁQUINAS I
 2004 V. BADIOLA
r = 2 = 0.05
d
40
→ GraficaA.26.9
D = 44 = 1.1
d
40
K t = 1.86
Análogamente se calcula se sensibilidad a la entalla q=0.9
Luego, K f = 1 + q ⋅ (K t − 1) = 1 + 0.9 ⋅ (1.86 − 1) = 1.774 El factor de concentración de tensiones
Kf’ a 103 ciclos es: K f = 1 + c ⋅ (K f − 1) siendo c =
'
0. 3 ⋅ S u
'
− 0.1 = 0.328 . Luego K f = 1.2543 .
700
❐ Efectos diversos Kg=1
❐ Factor de confiabilidad Kc: puesto que la resistencia Su=1000Mpa es una resistencia media y
por lo tanto se le asocia una confianza del 50%, calculamos este factor para una confianza del 90%.
K c = 1 − 0.08 ⋅ 1.3 = 0.896 .
A continuación, con todos los factores se calcula:
( )
S e 10 6 = K a ⋅ K b ⋅ K q ⋅ K d ⋅ K e ⋅ K g ⋅ K c ⋅ S 'e =
0.7231⋅ 0.9275 ⋅ 1⋅
1
⋅ 1⋅ 0.896 ⋅ 500 = 169.37MPa
1.774
Análogamente, la resistencia a 1000 ciclos se ve reducida por Kf’:
( )
S 10 3 =
0.9 ⋅ S ut
= 717.53MPa
Kf '
De esta forma queda definida la curva SN:
A 150.000 ciclos, la resistencia a la fatiga S se obtiene como:
log(717.53 ) − log(169.37 ) log(717.53 ) − log(S )
=
6−3
log(150000 ) − 3
S flexion = 251.8MPa
Límite de resistencia a la fatiga a torsión:
❐ Superficie Ka: K a = 4.51 ⋅ (1000 )−0.265 = 0.7231
❐ Tamaño Kb (d=40mm): K b =
DISEÑO DE MÁQUINAS I
d
7.62
−0.1133
= 0.8287 (sección completa)
- 160 -
 2004 V. BADIOLA
DPTO. INGENIERÍA MECÁNICA, ENERGÉTICA Y DE MATERIALES
❐ Carga Kq: 0.577 (torsión), pero luego no volveremos a multiplicarlo por 0.577 en la gráfica
siguiente:
❐ Concentración de tensiones: K e =
1
Kf
r = 2 = 0.05
d
40
→ GraficaA.26.8
D = 44 = 1.1
d
40
K t = 1.32
Análogamente se calcula se sensibilidad a la entalla q=0.98 (acero estirado)
Luego, K f = 1 + q ⋅ (K t − 1) = 1.3136 El factor de concentración de tensiones Kf’ a 103 ciclos es:
K f = 1 + c ⋅ (K f − 1) siendo c =
'
0. 3 ⋅ S u
− 0.1 = 0.328 . Luego K f ' = 1.1030 .
700
❐ Efectos diversos Kg=1
❐ Factor de confiabilidad Kc: puesto que la resistencia Su=1000Mpa es una resistencia media y
por lo tanto se le asocia una confianza del 50%, calculamos este factor para una confianza del 90%.
K c = 1 − 0.08 ⋅ 1.3 = 0.896 .
( )
S e 10 6 = K a ⋅ K b ⋅ K q ⋅ K d ⋅ K e ⋅ K g ⋅ K c ⋅ S 'e =
0.7231⋅ 0.8287 ⋅ 1⋅
1
⋅ 0.577 ⋅ 0.896 ⋅ 500 = 118MPa
1.3136
A 1000 ciclos:
0.72 ⋅ Su 0.72 ⋅ 1000
=
= 652.765MPa
Kf '
1.1030
Luego se obtiene a 200.000 ciclos:
log(652.765) − log(118) log(652.765) − log(S )
=
6−3
log(150000) − 3
S torsion = 188.76MPa
Cálculo de esfuerzos:
Sobre dicha sección tenemos (despreciamos el esfuerzo cortante):
A. Torsión: T = 10000 ⋅ 200 ± 2Pa ⋅ 200 + 5000 ⋅ 200 ± Pa ⋅ 200 = 3000000 ± 600Pa
- 161
DISEÑO DE MÁQUINAS I
 2004 V. BADIOLA
τa,max =
Ta ⋅ d / 2 16 ⋅ 600 ⋅ Pa 16 ⋅ 600 ⋅ Pa
=
=
= 0.047 ⋅ PaMPa
π ⋅ d4 / 32
π ⋅ d3
π ⋅ 403
τm,max =
Tm ⋅ d / 2 16 ⋅ Tm 16 ⋅ 3000000
=
=
= 238.7MPa
π ⋅ d4 / 32
π ⋅ d3
π ⋅ 403
B. Flexión alternada F = (10000 ± 2Pa ) − (5000 ± Pa ) = 5000 ± Pa
σa,max =
Ma ⋅ d / 2 32 ⋅ Ma 32 ⋅ 200Pa
=
=
= 0.032 ⋅ PaMPa
4
πd3
π403
πd
64
σm,max =
Mm ⋅ d / 2 32 ⋅ 5000 ⋅ 200
=
= 159.15MPa
4
π403
πd
64
Cálculo de Pa
La tensión media equivalente es la tensión media de Von-Mises:
σeqm =
(σ xm,flector )2 + 3 ⋅ (τxym )2
(159.15 )2 + 3 ⋅ (238.7)2
=
= 443MPa
Se calculan los factores α tomando como referencia la resistencia a la fatiga a flexión:
Flexión: α 1 = 1
Torsión: α 2 =
S N,flexion
S N,torsionl ⋅ 3
=
251.8
188.76 ⋅ 3
= 0.77
La tensión alternada equivalente es la tensión de Von-Mises, incluyendo los factores:
σ eqa =
(σ
)
2
xa ,flector
+ 3 ⋅ (τ xya ⋅ α 2 ) =
2
(0.032Pa )2 + 3 ⋅ (0.047 ⋅ Pa ⋅ 0.77)2
= Pa ⋅
(0.032)2 + 3 ⋅ (0.047 ⋅ 0.77)2
Pa ⋅ 0.07MPa
Se aplica ahora el criterio de Goodman:
σ eq,m
Su
+
σ eq,a
S N,flector
DISEÑO DE MÁQUINAS I
= 1→
443 0.07 ⋅ Pa
+
=1
1000
251.8
Pa = 2003N → 200.3kg
- 162 -
 2004 V. BADIOLA
DPTO. INGENIERÍA MECÁNICA, ENERGÉTICA Y DE MATERIALES
PROBLEMA 3
La pieza de la figura es de acero de 1000MPA de límite de rotura y 750Mpa de límite elástico,
totalmente rectificada. Está sometida a una carga constante vertical de 5000N y a un desequilibrio de
136gr·m que gira en el extremo libre de la barra.
Determinar la máxima velocidad de giro de la masa desequilibrada para que la pieza aguante a
fatiga 250.000 revoluciones.
Nota: calcular sólo la sección entallada. Se admite despreciar el esfuerzo axial.
z
x
Φ=44
r=2
Φ=40
y
302mm
5000N
300mm
La carga vertical de 5000N provoca sobre la sección crítica un momento flector Mx y un
momento torsor My (se desprecia el cortante).
My = 5000 ⋅ 300 = 1500000Nmm
Mx = 5000 ⋅ 300 = −1500000Nmm
La masa desequilibrada provoca una fuerza radial variable igual a la masa por la aceleración
normal:
D = M ⋅ w2 ⋅R
z
Fuerza desequilibrio=D
θ
y
- 163
DISEÑO DE MÁQUINAS I
 2004 V. BADIOLA
Dz = D ⋅ sinθ
D y = D ⋅ cos θ
My = −D ⋅ sinθ ⋅ 300
Mx = D ⋅ sinθ ⋅ 300
Mz = D ⋅ cos θ ⋅ 300
Se toma un punto cualquiera de la entalla, situado en un ángulo γ:
z
γ
x
Las tensiones sobre dicho punto son:
32 ⋅ 1500000 − d / 2 ⋅ sinγ ⋅ M x − d / 2 ⋅ cos γ ⋅ Mz
+
4
π ⋅ d3
π⋅d
64
32 ⋅ 1500000 − 32 ⋅ sinγ ⋅ M x − 32 ⋅ cos γ ⋅ M z
=
+
=
π ⋅ d3
π ⋅ d3
D ⋅ sinθ ⋅ sinγ + D ⋅ cos θ ⋅ cos γ
= 238.7 − 32 ⋅ 300 ⋅
π ⋅ 403
= 238.7 − 0.0477D ⋅ (sinθ ⋅ sinγ + cos θ ⋅ cos γ ) =
σ=
= 238.7 − 0.0477D ⋅ cos(θ − γ )
τ=
My ⋅ d / 2
π ⋅ d4 / 32
Luego el caso de mayor tensión se produce cuando cos(θ-γ)=-1. Esto es, cuando θ-γ=180º. Esto
implica que γ=θ-180º.
Como el coseno varía entre +1 y –1, la expresión será:
σ = 238.7 ± 0.0477D
Y por otro lado, la tensión a cortadura máxima es máxima para sin(θ)=±1. Esto es, la situación
de máxima tensión es para θ=±90º, y el punto de máxima tensión será el correspondiente a γ=±90º.
Puesto que el sino también varía entre +1 y –1, la expresión será:
τ=
16 ⋅ My
3
π⋅d
=
16 ⋅ 1500000 16 ⋅ 300 ⋅ D ⋅ sinθ
−
→ 119.3 ± 0.0238D
π ⋅ 403
π ⋅ 403
Límite de resistencia a la fatiga a flexión rotativa:
S e = K a ⋅ K b ⋅ K q ⋅ K d ⋅ K e ⋅ K g ⋅ K c ⋅ S 'e
DISEÑO DE MÁQUINAS I
- 164 -
DPTO. INGENIERÍA MECÁNICA, ENERGÉTICA Y DE MATERIALES
 2004 V. BADIOLA
Acero con Sut<1400Mpa, luego S'e = 0.5 ⋅ Sut = 500MPa .
Factores modificativos:
❐ Superficie Ka: K a = 1.58 ⋅ (1000 )−0.085 = 0.8783
d
❐ Tamaño Kb: K b =
7.62
−0.1133
= 0.828 .
❐ Carga Kq: en flexión rotativa este factor vale 1.
❐ Concentración de tensiones: K e =
r = 2 = 0.05
d
40
→ GraficaA.26.9
D = 44 = 1.1
d
40
1
Kf
K t = 1.86
Análogamente se calcula se sensibilidad a la entalla q=0.9
Luego, K f = 1 + q ⋅ (K t − 1) = 1 + 0.9 ⋅ (1.86 − 1) = 1.774 El factor de concentración de tensiones
Kf’ a 103 ciclos es: K f ' = 1 + c ⋅ (K f − 1) siendo c =
0.3 ⋅ S u
− 0.1 = 0.328 . Luego K f ' = 1.2543 .
700
❐ Efectos diversos Kg=1
❐ Factor de confiabilidad Kc: puesto que la resistencia Su=1000Mpa es una resistencia media y
por lo tanto se le asocia una confianza del 50%, calculamos este factor para una confianza del 90%.
K c = 1 − 0.08 ⋅ 1.3 = 0.896 .
A continuación, con todos los factores se calcula:
( )
S e 106 = K a ⋅ K b ⋅ K q ⋅ K d ⋅ K e ⋅ K g ⋅ K c ⋅ S 'e =
0.8783 ⋅ 0.828 ⋅ 1 ⋅
1
⋅ 1 ⋅ 0.896 ⋅ 500 = 183.6MPa
1.774
Análogamente, la resistencia a 1000 ciclos se ve reducida por Kf’:
( )
S 10 3 =
0.9 ⋅ S ut
= 717.53MPa
Kf '
De esta forma queda definida la curva SN:
- 165
DISEÑO DE MÁQUINAS I
 2004 V. BADIOLA
A 250.000 ciclos, la resistencia a la fatiga S se obtiene como:
log(717.53) − log(183.6) log(717.53) − log(S )
=
6−3
log(250000) − 3
S flexion = 241MPa
Límite de resistencia a la fatiga a torsión:
❐ Superficie Ka: K a = 1.58 ⋅ (1000 )−0.085 = 0.8783
❐ Tamaño Kb (d=40mm): K b =
d
7.62
−0.1133
= 0.8287 (sección completa)
❐ Carga Kq: 0.577 (torsión), pero luego no volveremos a multiplicarlo por 0.577 en la gráfica
siguiente:
❐ Concentración de tensiones: K e =
r
=2
1
Kf
= 0.05
40
→ GraficaA.26.8
D = 44
= 1 .1
d
40
d
K t = 1.32
Análogamente se calcula se sensibilidad a la entalla q=0.98 (acero estirado)
DISEÑO DE MÁQUINAS I
- 166 -
 2004 V. BADIOLA
DPTO. INGENIERÍA MECÁNICA, ENERGÉTICA Y DE MATERIALES
Luego, K f = 1 + q ⋅ (K t − 1) = 1.3136 El factor de concentración de tensiones Kf’ a 103 ciclos es:
K f = 1 + c ⋅ (K f − 1) siendo c =
'
0.3 ⋅ S u
'
− 0.1 = 0.328 . Luego K f = 1.1030 .
700
❐ Efectos diversos Kg=1
❐ Factor de confiabilidad Kc: puesto que la resistencia Su=1000Mpa es una resistencia media y
por lo tanto se le asocia una confianza del 50%, calculamos este factor para una confianza del 90%.
K c = 1 − 0.08 ⋅ 1.3 = 0.896 .
( )
Se 106 = K a ⋅ K b ⋅ K q ⋅ K d ⋅ K e ⋅ K g ⋅ K c ⋅ S'e =
0.8783 ⋅ 0.8287 ⋅ 1⋅
1
⋅ 0.577 ⋅ 0.896 ⋅ 500 = 143.2MPa
1.3136
A 1000 ciclos:
0.72 ⋅ Su 0.72 ⋅ 1000
=
= 652.765MPa
Kf '
1.1030
Luego se obtiene a 250.000 ciclos:
log(652.765 ) − log(143.2) log(652.765 ) − log(S )
=
6−3
log( 250000 ) − 3
S torsion = 194.16MPa
Criterio de Goodman
Se calculan los factores α tomando como referencia la resistencia a la fatiga a flexión:
Flexión: α1 = 1
Torsión: α 2 =
SN,flexion
SN,torsionl ⋅ 3
=
241
= 0.72
194.16 ⋅ 3
La tensión media equivalente es la tensión media de Von-Mises:
La tensión alternada equivalente es la tensión de Von-Mises, incluyendo los factores:
σeqm =
(σ xm,flector )2 + 3 ⋅ (τxym )2
σeqa =
(σ
)
2
xa , flector
=
(238.7)2 + 3 ⋅ (119.3)2
+ 3 ⋅ (τ xya ⋅ α 2 ) =
2
= 315.7MPa
(0.0477D)2 + 3 ⋅ (0.0238D ⋅ 0.72)2
= 0.0014D
Se aplica ahora el criterio de Goodman:
σeq,m
Su
+
σeq,a
SN,flector
=1→
315.7 0.0014D
+
= 1 → D = 117797N
1000
241
Como:
D = M ⋅ w2 ⋅R
Entonces,
D = M ⋅ w2 ⋅ R
117797 = 0.136 ⋅ w 2 → w = 930rad / s
- 167
DISEÑO DE MÁQUINAS I
 2004 V. BADIOLA
PROBLEMA 4
Un elemento de máquina está
sometido a una fuerza constante en amplitud,
pero que se desplaza periódicamente entre
dos puntos A y B. Durante el servicio se ha
comprobado que la pieza soporta 50.000
ciclos de desplazamiento de la carga entre A
y B. Sabiendo que la zona de la pieza en
voladizo está mecanizada y el resto puede
considerarse en bruto de forja, y que además
el material es acero de resistencia
Su=800Mpa y límite elástico Sy=650Mpa, estimar la carga aplicada según Goodman.
Considerar la concentración de tensiones como concentrador de tensiones y no reductor de
resistencia.
PROBLEMA 5
Sobre el elemento mecánico de la figura actúa una carga variable 5 6 P ± 16 P , y un torsor
constante T. Considerando que se desea una vida de diseño de 100.000 ciclos, determinar cuál es
coeficiente de seguridad para un nivel de confianza del 90%.
El material es acero con Sut=1000Mpa y Sy=750Mpa.
Emplear el criterio de Goodman y el criterio de Gerber.
D
L
r
5/6P±1/6P
d
L
L/2
2L
T
Datos:
L=300mm
d=40mm
DISEÑO DE MÁQUINAS I
- 168 -
DPTO. INGENIERÍA MECÁNICA, ENERGÉTICA Y DE MATERIALES
 2004 V. BADIOLA
D=44mm
r=2mm
P=T/L
P=1000N
Los factores a y b para el cálculo del coeficiente modificativo de fatiga corresponden a una
superficie rectificada, y son a=1.58 y b=-0.085.
- 169
DISEÑO DE MÁQUINAS I
 2004 V. BADIOLA
PROBLEMA 6
En el eje giratorio de la figura actúan dos cargas F1=45kgr y F2=140kgr, y una carga de
desequilibrio de 1300kgr·m que gira con el eje. Entre F1 y F2 existe un par torsor de valor
MT=5000cm·kgr.
El eje está soportado en sus extremos por dos rodamientos.
La superficie del eje está mecanizada, y el eje se debe dimensionar para vida infinita con un 90%
de seguridad funcional y empleando la línea de fallo de Gerber. Considerar CS=1.5.
Determinar el diámetro D del eje.
Considerar como secciones críticas aquellas donde se aplican las cargas puntuales.
a1=100mm
b1=300mm
a2=250mm
E=210Gpa
Sy=3800kgr·cm
Su=4500kgr·cm
Velocidad de giro=15 rpm
DISEÑO DE MÁQUINAS I
- 170 -
DPTO. INGENIERÍA MECÁNICA, ENERGÉTICA Y DE MATERIALES
 2004 V. BADIOLA
A1.5. PROBLEMAS TEMA 5:
PROBLEMA 1
La figura representa un eje en voladizo con dos volantes calados de peso P. El peso propio del
eje se desprecia. Considérese E módulo de elasticidad, I momento de inercia del eje.
Se pide calcular la primera velocidad crítica del eje:
Por el método de Rayleigh
Por el método de Dunkerley
Nota: Para facilitar los cálculos se da la ecuación de la deformación (elástica) en flexión para una
viga en voladizo:
y=
- 171
P L ⋅ x2 x3
⋅
−
EI
2
6
DISEÑO DE MÁQUINAS I
 2004 V. BADIOLA
Método de Rayleigh
w c1 =
g⋅
Wn ⋅ δn
Wn ⋅ δn
g ⋅ (W1 ⋅ y1 + W2 ⋅ y 2 )
(W ⋅ y
=
2
1
2
1
+ W2 ⋅ y 2
2
)
Como W1=W2=P,
w c1 =
g ⋅ (P ⋅ y1 + P ⋅ y 2 )
(P ⋅
2
y1
+ P ⋅ y2
2
)
g ⋅ (y1 + y 2 )
(y
=
2
1
+ y2
2
)
Los desplazamientos (y=δ) se plantean como:
y1 = a11 ⋅ Fc1 + a12 ⋅ Fc 2 = (a11 + a12 ) ⋅ P
y 2 = a21 ⋅ Fc1 + a22 ⋅ Fc 2 = (a 21 + a 22 ) ⋅ P
Con lo que se deben calcular los coeficientes de influencia:
a11 =
1 a ⋅ a2 a3
a3
⋅
−
=
EI
2
6
3EI
a22 =
1 2a ⋅ (2a )
(2a)
⋅
−
EI
2
6
a12 = a21 =
2
3
=
8a3
3EI
1 2a ⋅ a2 a3
5a3
⋅
−
=
EI
2
6
6EI
Así,
y1 = (a11 + a12 ) ⋅ P =
a3 5a3
7a3
+
⋅P =
P
3EI 6EI
6EI
y 2 = (a21 + a22 ) ⋅ P =
5a3 8a3
7a3
+
⋅P =
P
6EI 3EI
2EI
Y sustituyendo en la expresión de la velocidad crítica:
g⋅
w c1 =
7a 3
7a 3
P+
P
6EI
2EI
g⋅
w c1 =
2
7a 3
P
6EI
a3
P
EI
DISEÑO DE MÁQUINAS I
7a 3
+
P
2EI
2
a3
7 7
P⋅
+
EI
6 2
2
⋅
7
6
2
7
+
2
2
=
7 7
+
6 2
a3
P ⋅
EI
7
6
2
7
+
2
2
- 172 -
 2004 V. BADIOLA
DPTO. INGENIERÍA MECÁNICA, ENERGÉTICA Y DE MATERIALES
w c1 =
=
EI
3
a ⋅P
⋅
7 7⋅3
+
6 2⋅3
=
49 49 ⋅ 9
+
36 4 ⋅ 9
EI
14 ⋅ 36
⋅
=
490 ⋅ 3
a ⋅P
3
EI
3
a ⋅P
⋅
28
6 =
490
36
EI
3
a ⋅P
⋅
14
3 =
490
36
EI
12
⋅
35
a ⋅P
3
Método de Dunkerley
Aplicando este método:
1
w c1
2
=
Y como w =
1
w c1
2
1
w1
2
+
1
w2
2
g
g
→ w 2 = , sustituyendo en la expresión anterior,
δ
δ
= a11m1 + a 22 m 2 = a11 ⋅
P
P
+ a 22 ⋅
g
g
Y sustituyendo los valores aii:
1
w c1
2
a3
8a 3
⋅P +
⋅P
3a 3
3EI
= 3EI
=
⋅P
g
EIg
Con lo que:
w c1 =
- 173
EIg
3Pa 3
DISEÑO DE MÁQUINAS I
 2004 V. BADIOLA
PROBLEMA 2
Las dos masas de la figura M1 y M2 unidas al eje pesan 63.5kg y 27kg respectivamente.
Mediante un análisis en deformaciones y teniendo en cuenta que los coeficientes de influencia son los
indicados a continuación, calcular la velocidad crítica del eje.
a11 = 1.12 ⋅ 10 −5 cm / kg
a 22 = 6.72 ⋅ 10 −5 cm / kg
a12 = a 21 = 2.24 ⋅ 10 −5 cm / kg
Previo a resolver el problema, planteamos la coherencia de unidades. Las unidades de los
L
m
=
, en SI, con lo que asumiendo por simplicidad g≈10m/s2:
F
N
coeficientes aij son
a11 = 1.12 ⋅ 10 −8 m / N
a 22 = 6.72 ⋅ 10 −8 m / N
a12 = a 21 = 2.24 ⋅ 10 −8 m / N
Método de Rayleigh
Según este método,
w c1 =
g⋅
Wn ⋅ δn
Wn ⋅ δn
2
=
g ⋅ (W1 ⋅ y1 + W2 ⋅ y 2 )
(W ⋅ y
1
2
1
+ W2 ⋅ y 2
2
)
Así,
y 1 = a11 ⋅ W1 + a12 ⋅ W2 = 1.12 ⋅ 10 −8 ⋅ 63.5 ⋅ 10 + 2.24 ⋅ 10 −8 ⋅ 27 ⋅ 10 = 13.16 ⋅ 10 −6 m
y 2 = a 21 ⋅ W1 + a 22 ⋅ W2 = 2.24 ⋅ 10 −8 ⋅ 63.5 ⋅ 10 + 6.72 ⋅ 10 −8 ⋅ 27 ⋅ 10 = 32.368 ⋅ 10 −6 m
Y sustituyendo en la expresión anterior:
w c1 =
g ⋅ (W1 ⋅ y 1 + W2 ⋅ y 2 )
(W ⋅ y
1
(
1
2
+ W2 ⋅ y 2
2
)=
10 ⋅ 63.5 ⋅ 10 ⋅ 13.15 ⋅ 10 −6 + 27 ⋅ 10 ⋅ 32.368 ⋅ 10 −6
=
(
63.5 ⋅ 10 ⋅ 13.15 ⋅ 10
)
−6 2
(
+ 27 ⋅ 10 ⋅ 32.368 ⋅ 10
)
)
−6 2
= 659.7rad / s
Método de Dunkerley
Según este método,
1
w c1
2
=
1
w1
DISEÑO DE MÁQUINAS I
2
+
1
w2
2
- 174 -
DPTO. INGENIERÍA MECÁNICA, ENERGÉTICA Y DE MATERIALES
O lo que es lo mismo, como w =
1
w c1
2
=
 2004 V. BADIOLA
g
g
→ w2 = .
δ
δ
δ11 δ 22 a11W1 + a 22 W 2
+
=
= a11M1 + a 22M 2 =
g
g
g
= 1.12 ⋅ 10 −8 ⋅ 63.5 + 6.72 ⋅ 10 −8 ⋅ 27 = 2.525610 −6
Luego, w c1 = 629.2rad / s
PROBLEMA 3
El eje de acero de la figura tiene unidos dos engranajes cuyos pesos son 45.4kg y 22.7kg
respectivamente. Despreciando la masa del eje determinar la primera velocidad crítica. Nota: x=25.4m,
d=20.3m
Problema 4
Para un eje biapoyado, de sección circular de diámetro D (m)y espesor t (m), realizado en acero
con densidad ρ (kg/m3). Se desea determinar la longitud L de eje admisible para si se desea que el eje
opere a n rad/s. Módulo de Young E (Pa)
Resolución:
Para un eje sin masas adicionales, se deduce que:
wc =
5 g
⋅
4 δ max
(1)
δmax
Se debe calcular la máxima flecha, esquematizando el eje como un eje de longitud L (variable a
determinar) que soporta una carga distribuida q:
- 175
DISEÑO DE MÁQUINAS I
 2004 V. BADIOLA
La carga q corresponde con el cociente entre el peso total del eje (volumen*densidad*g) y la
longitud del eje:
(
)
π ⋅ D 2 − (D − 2t )2 ⋅ L ⋅ ρ ⋅ g
[N / m] (2)
q= 4
L
Se parte de la ecuación de la elástica y mediante integración se obtienen las flechas (y). La
expresión de M(x) es:
M( x ) =
q⋅L
q
q ⋅L ⋅ x q ⋅ x2
⋅ (L − x ) − ⋅ (L − x ) 2 =
−
2
2
2
2
Con lo que integrando la ecuación siguiente: −
El momento de inercia es: I =
(
M d2 y
=
EI dx 2
π 4
4
D − (D − 2t )
64
)
Se obtiene:
y( x ) = −
(
q⋅ x
2Lx − x 3 − L
24EI
)
3
Y para x=L/2,
y(L / 2) = δ max =
5 ⋅ q ⋅ L4
348EI
Sustituyendo en esta última expresión la (2),
δ max
(
)
π ⋅ D 2 − (D − 2t )2 ⋅ L ⋅ ρ ⋅ g
5L4
= 4
⋅
= A(cte) ⋅ L4
L
348EI
Así, queda la expresión (1) en función de la variable L.
Puesto que el eje debe trabajar a n rad/s, se hace que n=0.6·wcrit. Y así, de esta última expresión
se despeja la longitud L.
DISEÑO DE MÁQUINAS I
- 176 -
DPTO. INGENIERÍA MECÁNICA, ENERGÉTICA Y DE MATERIALES
 2004 V. BADIOLA
A1.6. PROBLEMAS TEMA 6:
PROBLEMA 1
El elemento de un reductor de velocidad que se indica en la figura siguiente está dispuesto para
que giren las copas de los rodamientos y los conos permanezcan estacionarios. El rodamiento A
soporta una carga de empuje de 250lb y además tiene una carga radial de 875lb. El rodamiento B
resiste una carga radial pura de 625lb. La velocidad de rotación es de 150rev/min. La vida L10 deseada
es de 90.000horas. Obsérvese que esto equivala a decir que se desea una vida de 90.000 horas con
una confiabilidad del 90%. Los diámetros de eje deseados son 11/8 “ para A y 1”para B. Seleccione los
rodamientos de rodillos cónicos apropiados, empleando un factor de seguridad igual a la unidad.
Se emplea un valor de prueba o tanteo de 1.5 para ambos valores de K:
La carga de empuje en A aumenta mediante la carga de empuje inducida proveniente de B.
PA = 0.4 ⋅ FrA + K A ⋅
PA = 0.4 ⋅ 875 + 1.5 ⋅
0,47 ⋅ FrB
+ Fae
KB
(1)
0,47 ⋅ 625
+ 250 = 1020Lb
1 .5
Puesto que PA = 1020Lb > FrA = 875Lb , se emplea 1020Lb como la carga radial equivalente
para seleccionar el rodamiento A.
Se aplica la siguiente ecuación para obtener la vida L10, y como se muestra en la figura 11-10
(columnas 4 y 5), la designación de Timken es de L10 igual a 3000h a 500rpm.
N
FR = FD ⋅ D
NR
1/ p
L ⋅n
= FD ⋅ D D
L R ⋅ nR
90.000 ⋅ 150
FR = 1020 ⋅
3000 ⋅ 500
1/ p
(2)
3 / 10
= 1970Lb
Utilizando esta cantidad y un diámetro interior de rodamiento de 11/8 “se entra en el catálogo
(Figura 11-10) y se selecciona un cono 15590 y una copa 15520, ya que tiene los menores valores de
capacidad, diámetro exterior y ancho Esta selección tiene KA=1.69, y una capacidad de 2480Lb. La
diferencia con el valor supuesto de 1.5 es pequeña y no se calculará de nuevo la carga radial PA.
En el caso del rodamiento B,
- 177
DISEÑO DE MÁQUINAS I
 2004 V. BADIOLA
PB = 0.4 ⋅ FrB + K B ⋅
0,47 ⋅ FrA
− Fae
KA
PB = 0.4 ⋅ 625 + K B ⋅
0,47 ⋅ 875
− 250 = 240Lb
1.69
Obsérvese que se ha empleado el valor real de KA pero se supuso que KB=1.5 como antes. En
este caso, PB = 240Lb < FrB = 625Lb , de modo que se emplea FrB como la carga efectiva. Utilizando
de nuevo la ecuación de vida pero en este caso para el rodamiento B:
FR = FD ⋅
ND
NR
FR = 625 ⋅
1/ p
= FD ⋅
L D ⋅ nD
L R ⋅ nR
90.000 ⋅ 150
3000 ⋅ 500
1/ p
3 / 10
= 1210Lb
Este rodamiento tiene un diámetro interior de 1”. Si se emplea la figura 11-10 para la selección,
hay cinco rodamientos a elegir. Se escogen el cono 23100 y la copa 23256 puesto que tiene los
menores valores de capacidad, diámetro exterior y ancho. La capacidad es de 2950Lb con K=0.8.
A continuación, con los valores correctos de K se calculan de nuevo las expresiones (1) y (2):
PA = 0.4 ⋅ 875 + 1.69 ⋅
FR = 1393 ⋅
0,47 ⋅ 625
+ 250 = 1393Lb
0.8
90.000 ⋅ 150
3000 ⋅ 500
3 / 10
= 2690Lb
El rodamiento A seleccionado antes tenía una capacidad de 2480Lb, con lo que no sería
suficiente, y los rodamientos que aparecen en el catálogo para el tamaño de eje deseado no cumplen
con el nuevo requerimiento de capacidad. Sin embargo, lo que se debe tener en cuenta es que este
aumento en la carga efectiva de A ha sido debido al bajo valor de KB=0.8. Por ello, si seleccionamos
como rodamiento B el correspondiente al cono 02473 y copa 02420, tenemos por un lado, que la
capacidad no aumenta excesivamente respecto a la aplicación de B, y, en consecuencia el tamaño, y
por otro lado, el factor KB=1.4, valor cercano a la hipótesis inicial de 1.5:
PA = 0.4 ⋅ 875 + 1.69 ⋅
0,47 ⋅ 625
+ 250 = 1127Lb
1.4
90.000 ⋅ 150
FR = 1127 ⋅
3000 ⋅ 500
3 / 10
= 2177Lb
Que resulta satisfactorio para el rodamiento A seleccionado.
Conclusión:
Rodamiento A: cono 15590, copa 15520
Rodamiento B: cono 02473, copa 02420
DISEÑO DE MÁQUINAS I
- 178 -
DPTO. INGENIERÍA MECÁNICA, ENERGÉTICA Y DE MATERIALES
 2004 V. BADIOLA
Anejo 2. Tablas y
Gráficos
- 179
DISEÑO DE MÁQUINAS I
 2004 V. BADIOLA
DISEÑO DE MÁQUINAS I
- 180 -
DPTO. INGENIERÍA MECÁNICA, ENERGÉTICA Y DE MATERIALES
- 181
 2004 V. BADIOLA
DISEÑO DE MÁQUINAS I
 2004 V. BADIOLA
DISEÑO DE MÁQUINAS I
- 182 -
DPTO. INGENIERÍA MECÁNICA, ENERGÉTICA Y DE MATERIALES
- 183
 2004 V. BADIOLA
DISEÑO DE MÁQUINAS I
 2004 V. BADIOLA
DISEÑO DE MÁQUINAS I
- 184 -
DPTO. INGENIERÍA MECÁNICA, ENERGÉTICA Y DE MATERIALES
- 185
 2004 V. BADIOLA
DISEÑO DE MÁQUINAS I
 2004 V. BADIOLA
DISEÑO DE MÁQUINAS I
- 186 -