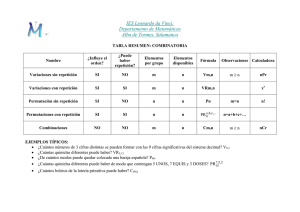
PRACTICA de ANÁLISIS COMBINATORIO

ANÁLISIS COMBINATORIO
I. ENCIERRA LA LETRA DE LA ALTERNATIVA CORRECTA.
1. Es la rama de la matemática que estudia los diversos arreglos o selecciones que podemos formar con
los elementos de un conjunto dado.
a) Permutaciones
b) Combinaciones
c) Variaciones
d) Análisis Combinatorio
2. De acuerdo al principio fundamental del conteo, si un hecho ocurre de m manera distinta, otro hecho n
independiente ocurre de n maneras distintas y un tercer hecho ocurre de r maneras distintas entonces el
número de maneras posibles en los que pueden ocurrir los hechos es el resultado de:
3. A un conjunto por cada una de las posibles ordenaciones de todos los elementos de dicho conjunto.
a) Permutaciones
b) Combinaciones
c) Variaciones
d) Análisis Combinatorio
4. Es un arreglo de elementos en donde no nos interesa el lugar o posición que ocupan los mismos dentro
del arreglo.
a) Permutaciones
b) Combinaciones
c) Variaciones d) Análisis Combinatorio
VARIACIONES SIN REPETICION
I. ENCIERRA LA LETRA DE LA ALTERNATIVA CORRECTA.
1. Son los diferentes grupos que pueden formarse con los N elementos dados, tomados de n en n, de modo que dos
grupos difieren entre sí cuando, al menos, un elemento es distinto
a) Permutaciones
b) Combinaciones
c) Variaciones
d) Análisis Combinatorio
2. Son los distintos grupos de n elementos distintos que se pueden hacer con los m elementos que
tenemos, de forma que dos grupos se diferencian en algún elemento o en el orden de colocación.
a) Permutaciones con repetición
b) variaciones con repetición
c) Variaciones sin repetición d) permutaciones sin repetición
3. Son los distintos grupos de n elementos iguales o distintos que se pueden hacer con los m elementos
que tenemos, de forma que dos grupos se diferencian en algún elemento o en el orden de colocación.
a) Permutaciones con repetición
c) Variaciones sin repetición
b) variaciones con repetición
d) permutaciones sin repetición
www.edicioneszorrilla.com.do Refuerzo en mat para 4to de media. Cristo murió por mí en la cruz
1
DETERMINE EN CADA CASO EL VALOR DE m: Ver ejemplos en www.edicioneszorrilla.com.do
RESOLVER LOS SIGUIENTES PROBLEMAS DE VARIACIONES SIN REPETICIÓN
1. De cuantas formas diferentes pueden sentarse 5 personas en 8 sillas.
2. Cuantas señales de por lo menos 3 banderas pueden hacerse en un asta con 6 banderas de colores
diferentes.
3 Cuantas señales de 3 banderas pueden hacerse en un asta con 6 banderas de colores diferentes.
4 ¿Cuántas señales con no más de 3 banderas pueden hacerse con 6 banderas de colores diferentes.
5. Con las letras a, b, c, d, e; ¿Cuántas ordenaciones de 3 letras diferentes pueden formarse?
6. Con las letras de la palabra Cristo. ¿Cuántas ordenaciones de 4 letras diferentes pueden formarse de
modo que la C sea siempre la segunda letra?
7. Un club deportivo dispone de 8 voluntarios para formar su directiva. Si los cargos de esta son
Presidente, Tesorero, Secretario y Vocal. ¿De cuantas formas pueden ser ocupados?
8. ¿Cuántos números de 3 cifras se pueden formar con las cifras 1, 2, 3, 4, 5, 6, 7, 8, 9 sin repetir ninguna
cifra?
9. Con las letras de la palabra orquídea cuantas ordenaciones se pueden hacer, de modo que ninguna
consonantes este al principio o al final.
VARIACIONES CON REPETICIÓN
Ver ejemplos en www.edicioneszorrilla.com.do
www.edicioneszorrilla.com.do Refuerzo en mat para 4to de media. Cristo murió por mí en la cruz
2
RESOLVER LOS SIGUIENTES PROBLEMAS DE VARIACIONES CON REPETICIÓN
1. Con los números 1, 2, 3,4. ¿Cuántos números de 3 cifras se pueden formar?
2. Entre Santo Domingo y Santiago hay 4 compañías de trasporte. ¿De cuantas formas puede hacer el
viaje de ida y vuelta una persona desde Santo Domingo o Santiago?
3. Con las cifras del número 1986 ¿Cuántos números de 3 cifras puede formarse de modo que el 8 ocupe
siempre el lugar de las centenas?
4. Una nueva Compañía Telefónica ha decidido implementar en el país 6 nuevos código con el código de
área 849, INDOTEL le ha asignado los números (500, 503, 508, 509, 529, 529). ¿Cuántos números
telefónicos pueden se le van a suministrar a la población con dichos códigos?
PERMUTACIONES SIN REPETICIÓN
I. ENCIERRA LA LETRA DE LA ALTERNATIVA CORRECTA.
1. Son los distintos grupos de n elementos distintos que se pueden hacer, de forma que dos grupos se
diferencian únicamente en el orden de colocación
a) Permutaciones con repetición
b) variaciones con repetición
c) Variaciones sin repetición
d) permutaciones sin repetición
2. Son los distintos grupos de n elementos que se pueden hacer de forma que en cada grupo, cada
elemento aparezca el número de veces indicado y que dos grupos se diferencian únicamente en el orden
de colocación.
a) Permutaciones con repetición
b) variaciones con repetición
c) Variaciones sin repetición
d) permutaciones sin repetición
Resolver los siguientes ejercicios. Ver ejemplos en www.edicioneszorrilla.com.do
RESOLVER LOS SIGUIENTES PROBLEMAS DE PERMUTACIÓN SIN REPETICIÓN
1. ¿De cuántas formas pueden sentarse 5 niños/as en un banco?
2. ¿De cuántas formas pueden sentarse 5 niños/as en un banco si 2 de ellos deben sentarse siempre juntos?
3. ¿Cuántos grupos de letras se formarán con las letras de la palabra Isabel, con tal que no vayan ni dos
vocales ni dos consonantes juntas? ¿Cuántos de esos grupos comenzarán por vocal?
4. ¿De cuantas formas se pueden sentar 3 niños y 2 niñas de modo que queden alternados?
www.edicioneszorrilla.com.do Refuerzo en mat para 4to de media. Cristo murió por mí en la cruz
3
5. Un empleado de un supermercado debe colocar 7 marcas diferentes de arroz en un tramo de un
escaparate. ¿De cuántas formas podría colocarlos?
6. ¿De cuántas formas diferentes pueden colocarse las letras de la palabra murciélago?
7. ¿De cuántas formas podríamos sentar seis niños (3 niños y 3 niñas) en un sillón de
siempre se sienten siempre los tres niños y las tres niñas juntas?
modo que
8. ¿De cuántas formas podríamos sentar seis niños (3 niños y 3 niñas) en sillones separados de modo que
siempre se sienten siempre los tres niños y las tres niñas juntas?
9. Los miembros de una familia: Padre, Madre, 3 hijos y 2 sobrinos deben sentarse en una mesa
rectangular de tal forma que los padres siempre estén en los extremos. ¿De cuántas formas podrán
hacerlo?
PERMUTACIONES CON REPETICION
RESOLVER LOS SIGUIENTES PROBLEMAS DE PERMUTACIÓN CON REPETICIÓN
1. ¿De cuántas formas pueden colocarse las letras de la palabra MARACA?
2. Con las letras de la palabra MARACA ¿Cuántas ordenaciones de 6 letras se forman que no comiencen
ni terminen con A?
3. ¿De cuantas maneras pueden colocarse las letras de la palabra MATEMATICAS?
4. ¿Cuántas permutaciones distintas podremos formar utilizando cada vez todas las letras de la palabra
vivir?
COMBINACIONES
1. Resolver los siguientes ejercicios. Ver ejemplos en www.edicioneszorrilla.com.do
2. RESOLVER LOS SIGUIENTES PROBLEMAS
1. ¿Cuántas rectas pueden trazarse por 18 puntos coplanares si nunca 3 de ellos están en línea recta?
2. ¿Cuántas diagonales pueden trazarse en un polígono de 12 lados?
3. Una agencia de viaje ofrece un plan de visitar tres capitales de América Central, de un universo de 7
países. ¿Cuántas ofertas puede hacer?
4. Se desea saber la cantidad de dinero que recaudará la LOTO. Si tiene cuarenta números y cada boleta
tiene seis números y cada boleta cuesta 25 pesos.
www.edicioneszorrilla.com.do Refuerzo en mat para 4to de media. Cristo murió por mí en la cruz
4
5. ¿Cuántos grupos de cinco podrán formarse con los 30 alumnos de una clase, en el supuesto de que un
grupo se diferencie de otro por lo menos en un alumno?
6. ¿Qué cantidad de dinero debe jugarse para sacarse la lotería LOTO de manera segura. Si tiene treinta y
seis números y cada boleta tiene seis números y cada boleta cuesta 30 pesos.
7. ¿De cuantas formas pueden mezclarse los sietes colores del arcoíris, tomándolo de tres en tres?
8. Un grupo compuesto por 5 hombres y 7 mujeres, forman un comité por 2 hombres y 3 mujeres.
De cuantas forma pueden formarse si: a) pueden pertenecer a cualquier hombre o mujer. b) Una mujer
determinada debe pertenecer al comité. c) Dos hombres determinados, no pueden estar en el comité.
BINOMIO DE NEWTON
1. DETERMINE EL DESARROLLO DEL BINOMIO A CONTINUACIÓN.
www.edicioneszorrilla.com.do
a) (2 x  y 2 ) 4
b) ( x 2  2 y) 5
c) ( x 2  y) 6
d) (4 x3  3 y 2 )5
2. DETERMINE EL TÉRMINO QUE TE PIDEN
a) ( x  y 2 )5
el término 5to.
c) ( x 2  2 y)7 Determine el término 8vo.
b) (2 x 2  y)4 término medio
d) ( x 2  y)14 Determine el término central
Todavía no he puesto trabajo en la web, si usted consigue
video, por favor mandármelo a
Al correo [email protected]
www.edicioneszorrilla.com.do Refuerzo en mat para 4to de media. Cristo murió por mí en la cruz
5