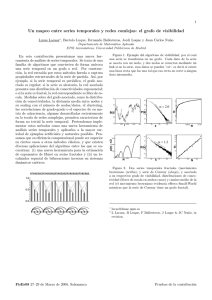
Representaciones topológica y de visibilidad de grafos

Representaciones topológica y de
visibilidad de grafos
M.C. Botebol, F.J. Cobos, J.C. Dana,
A. Márquez y F. Mateos
Dpto. de Matemática Aplicada I. Facultad de Informática y Estadı́stica. Universidad
de Sevilla. Avda. Reina Mercedes s/n. 41012-Sevilla. Tfno.:(95)-4552797. Fax:
(95)-4557878.
Email: {botebol,cobos,dana,almar,mateos}@obelix.cica.es.
Resumen
El presente trabajo establece las bases para el estudio de las relaciones
existentes entre las representaciones topológica y de visibilidad de grafos
en el plano. Además, se prueba que cualquier grafo admite una representación de visibilidad sobre alguna superficie, lo que nos va a permitir
generalizar los resultados obtenidos para el plano.
Palabras clave: grafos, superficies, representación topológica, representación de visibilidad, inmersión, género.
1
Introducción
La manera usual de representación de grafos es la topológica, la cual asocia sus
vértices a puntos del plano o del espacio y sus aristas a curvas de Jordan que
unen dichos puntos. Esta forma de representación es muy práctica, entre otros
motivos, por permitir la utilización de gran cantidad de herramientas y resultados topológicos conocidos. Sin embargo, al no tener en cuenta la naturaleza
combinatoria de los grafos, una cantidad infinita de ellos comparten una misma
representación.
Recientemente se han propuesto algunas otras formas de representación
(grafos de intersección, de intervalos, enrejados, etc.). En general son formas
de representación basadas en el concepto de visibilidad, las cuales presentan la
ventaja de ser las más cercanas a las estructuras combinatorias que representan. Además, producen mejores modelizaciones para el estudio de aplicaciones
gráficas que el modelo topológico (supóngase el movimiento de un robot que
sólo pueda desplazarse en las direcciones de los ejes coordenados o el trazado
de circuitos impresos que se realiza mediante desplazamientos horizontales y
verticales de un brazo articulado).
Evidentemente, en este caso no disponemos del bagaje de resultados existentes en el caso topológico. Quizás el resultado más satisfactorio, en este sentido, sea el teorema de caracterización de bar-visibilidad obtenido por Tamassia
y Tollis [6] e, independientemente, por Wismath [11].
En un grafo de bar-visibilidad o bar-representación de un grafo, los vértices
están representados por segmentos (barras) horizontales y dos vértices están
conectados por una arista si sus barras correspondientes pueden verse entre sı́
verticalmente y de forma no degenerada.
Probablemente, el primer trabajo relacionado con representaciones planas
de grafos es la fórmula de Euler, que es todavı́a uno de los resultados fundamentales en el estudio de representaciones planas, al menos, en su formulación de
Cauchy (ver [1]). Desde la publicación del teorema de Kuratowski han aparecido
muchos trabajos relacionados con la naturaleza de las inmersiones de un grafo
en el plano. Por dar dos ejemplos, podemos citar, el teorema de Whitney [10]
que prueba que la inmersión de un grafo 3-conexo es única en la superficie de
la esfera y el estudio de la peri-planaridad de grafos realizado por Chartrand y
Harary [2].
Sin embargo, se conoce muy poco sobre la estructura de las representaciones de visibilidad de grafos en el plano (menos aún sobre representaciones de
visibilidad en otras superficies). El propósito del presente trabajo es plantear
diversas cuestiones (e intentar resolver algunas de ellas) sobre las relaciones en-
tre ambos tipos de representación. De hecho, el primer resultado en este sentido
es el teorema de caracterización de los grafos bar-planos.
Teorema 1. [11, Wismath][6, Tamassia y Tollis] Una inmersión plana de un
grafo procede de una bar-representación si, y sólo si, sus puntos de corte se
encuentran en la cara externa.
Resultados similares han sido establecidos para la esfera [7] y el cilindro [8].
Podemos entonces decir que, estos teoremas, relacionan ambos tipos de representación en el sentido que va de la topológica a la de visibilidad. En la siguiente
sección daremos algunos resultados en el sentido inverso.
2
De la representación de visibilidad a la topológica
Dado un grafo plano G (un grafo es plano si admite una inmersión en el plano),
decimos que dos inmersiones de G son equivalentes si existe una holonomı́a plana
de una inmersión en la otra es decir, si se puede pasar de una representación
a la otra mediante movimientos y/o deformaciones sin salirse del plano (una
inmersión plana es denominada, con frecuencia, como un grafo plano). La Figura 1 nos muestra dos inmersiones no equivalentes de un mismo grafo, ya que
si nos fijamos en el vértice v podemos observar que las listas de sus vértices adyacentes descritas en el sentido de las agujas del reloj son {1, 3, 4, 2} y {1, 2, 4, 3}
respectivamente. Es decir, hemos variado la secuencia de los vértices adyacentes
a v y, por tanto, es necesario salirse del plano para pasar de una inmersión a la
otra por lo que las inmersiones no son equivalentes.
2
2
s
s
4 s
v
s
sv
s
s
3
3
s
1
s4
s
1
Figura 1: Dos inmersiones no equivalentes de un mismo grafo.
En este sentido, desde la aparición del teorema de Whitney, sabemos que
un grafo 3-conexo y plano de f caras posee 2f inmersiones, no equivalentes, en
el plano (aunque sólo una en la esfera).
Figura 2: Dos ventanas entre v1 y v2 .
Denominamos ventana entre dos barras, en una bar-representación de un
grafo G (ver Figura 2), a cualquier rectángulo maximal que teniendo dos lados
(opuestos) situados en ambas barras produce intersección vacı́a con las demás
barras de G.
Decimos que una inmersión plana procede de una bar-representación si
existe una inmersión tal que sus vértices están situados en las correspondientes
barras y las aristas que unen dos vértices están (ver Figura 3) en una estrecha
banda situada alrededor de cada barra y en una de las ventanas existentes entre
ellas.
Figura 3: La situación de una arista entre dos vértices.
Una pregunta que surge de forma natural es cuándo una bar-representación induce una única inmersión topológica, que llamaremos canónica. A fin de
caracterizar las bar-representaciones canónicas daremos la siguiente definición:
llamamos esqueleto de una bar-representación φ de un grafo G (que representaremos por sk(φ)) a la inmersión plana del multigrafo que posee los mismos vértices
que G y tantas aristas, uniendo dos vértices, como ventanas aparecen entre ellos
en la referida bar-representación. Obviamente, una bar-representación induce
una única inmersión plana de tal multigrafo y contiene, en algún sentido, a to-
das las inmersiones de G que proceden de φ. De hecho, podemos asegurar el
siguiente resultado.
Proposición 2. Sea sk(φ) el esqueleto de una bar-representación φ de un grafo
G. Un grafo plano está inducido por φ si, y sólo si, es un grafo plano maximal
contenido en sk(φ). Además, dos grafos planos maximales contenidos en sk(φ)
no pueden ser equivalentes.
Demostración: La primera afirmación de la proposición es, obviamente, cierta.
Pero, dado que las ventanas entres dos barras son rectángulos maximales, dos
aristas que unen el mismo par de vértices en sk(φ) no pueden ser consecutivas,
por tanto, la segunda afirmación también es cierta.
Como consecuencia inmediata de la anterior proposición, obtenemos el siguiente corolario.
Corolario 3. Una bar-representación de un grafo es canónica si, y sólo si, su
esqueleto es un grafo y, además, una inmersión plana de dicho grafo.
Como consecuencia de la Proposición 2 y del Corolario 3 surgen, de manera
natural, algunas cuestiones como son si es posible construir, y con qué coste,
el esqueleto de una bar-representación dada y, como consecuencia, si es posible
modificar una bar-representación que no sea canónica para encontrar otra que
sı́ lo sea. Podremos responder a estas cuestiones con los siguientes resultados.
Proposición 4. El esqueleto de una bar-representación de un grafo de N vértices puede ser computado en tiempo O(N log N ).
Demostración: Sea φ una bar-representación de un grafo de N vértices y ordenemos, en primer lugar, de izquierda a derecha las coordenadas xi de los extremos
de las barras de φ. Usaremos un algoritmo de barrido del plano para encontrar
las ventanas existentes entre las barras de φ. Construiremos, en cada paso una
lista de las barras, ordenadas de arriba a abajo existentes en la franja vertical
que va de xi a xi+1 y discretizaremos el barrido a los puntos xi . Pueden darse
dos tipos de situaciones:
a) Añadimos una barra a nuestra lista (si el punto xi en estudio coincide
con uno de los extremos izquierdos de las barras). En este caso hemos
encontrado una ventana entre la nueva barra y las más cercanas en la lista
situadas por encima y por debajo de ella.
b) Eliminamos una barra de nuestra lista (si el punto es uno de los extremos
derechos). En este caso hemos encontrado una ventana entre las barras
más cercanas en la lista por encima y por debajo de la barra eliminada.
Concluimos la demostración viendo que la ordenación y clasificación (en
extremos izquierdos o derechos) de los extremos de las barras puede conseguirse
en tiempo O(N log N ) y el barrido puede mantenerse a un coste O(log N ) por
operación.
Proposición 5. Sea φ una bar-representación de un grafo plano G. Es posible obtener una bar-representación canónica de G cambiando sólo los extremos
izquierdos de algunas barras de φ. Además, esta operación puede realizarse en
tiempo O(N log N ).
Demostración: Podemos utilizar el algoritmo usado en la demostración de la
Proposición 4, pero cuando aparezca una segunda ventana entre dos barras la
eliminamos modificando las coordenadas de los extremos izquierdos de las barras
situadas entre ambas en la siguiente franja.
3
Más allá de la planaridad
Cuando un grafo no es plano se nos presentan dos opciones a la hora de dar una
representación topológica suya: o bien dar una inmersión en R3 o representarlo
en una superficie de superior género. Esta última solución es la más usual y
fructı́fera en la teorı́a topológica de grafos. No obstante, esta vı́a no ha sido
estudiada, aún, en representaciones de visibilidad (con excepción de algunos
resultados parciales de Tamassia y Tollis [6, 7, 8]). El propósito de esta sección es
probar que es posible obtener algún tipo de género para la visibilidad abriendo,
probablemente, bastantes problemas relacionados con este tema.
El primer problema al que nos enfrentamos es el de la obtención de representaciones de visibilidad en una superficie cualquiera. Naturalmente, la
primera herramienta que necesitamos es el conocido teorema de Clasificación de
Superficies (ver, por ejemplo, [4]).
Teorema 6. Toda superficie orientable, cerrada y conexa es homeomorfa a una
de las superficies poligonales estándares.
Donde las superficies poligonales estándares se obtienen identificando las
aristas de un 4n-gono siguiendo la estructura descrita en la siguiente Figura 4.
Pero, por otra parte observamos que, en todas caracterizaciones de grafos
bar-representables, es fundamental la existencia de un sistema ortogonal, de tal
forma que los objetos y la visibilidad entre ellos estén basados en dicho sistema
de referencia ortogonal. En otras palabras, las barras son paralelas y la visibilidad es ortogonal a ellas. Sin embargo, las superficies poligonales estándares
a
i
b
1
a
7
b
o
Figura 4: Una de las asas de una superficie de género n.
carecen de tal sistema de referencia ortogonal. No obstante, es posible dar otra
representación diferente de tales superficies y como consecuencia del Teorema 6
podemos dar el siguiente teorema de clasificación.
Teorema 7. Toda superficie orientable, cerrada y conexa es homeomorfa a una
de las superficies ortogonales estándares.
Donde las superficies ortogonales estándares de género n se obtienen identificando los lados opuestos de un rectángulo del que se han recortado de su
interior n − 1 pequeños rectángulos (también con sus lados opuestos identificados) siguiendo la estructura descrita en la Figura 5.
···
1
2
n−1
Figura 5: La superficie ortogonal estándar de género n.
En una superficie ortogonal estándar, llamamos id-rectángulos a los rectángulos eliminados (o recortados) del interior del rectángulo grande y cuyos lados
opuestos se encuentran identificados según nos muestra la Figura 5.
En este sentido, podemos decir que un grafo es bar-representable en una
superficie de género n, si los vértices están representados por barras horizontales
(arcos de paralelos) en la superficie ortogonal estándar de género n, y dos vértices
están conectados por una arista si sus barras correspondientes pueden verse
verticalmente (en la dirección de los meridianos) y de forma no degenerada.
Con estas definiciones podemos dar el siguiente resultado.
Teorema 8. Dado un grafo G, existe n ∈ N tal que G es bar-representable en
una superficie de género n.
Demostración: Probaremos el teorema mediante inducción en el número m de
vértices de G. La afirmación es obviamente cierta para valores pequeños de
m. Supongamos que el grafo G posee m vértices y que la afirmación es cierta
para grafos de menos de m vértices. Consideremos una bar-representación φ de
G−v en On (superficie ortogonal estándar de género n) y supongamos que On se
obtiene a partir del cuadrado unidad [0, 1]×[0, 1]. En ese caso, cada punto de On
se define mediante las coordenadas de uno de sus representantes. Seleccionemos
ahora x ∈ [0, 1] tal que la circunferencia [0, 1] × {x} tenga intersección vacı́a
con los id-rectángulos y con las barras que representan a los vértices de G − v y
trataremos de modificar dicha circunferencia y las otras barras a fin de encontrar
una bar-representación de G. Sean 0 < a1 < . . . < ak < 1 las abscisas de
todos los extremos de barras que representan vértices de G − v ası́ como de
puntos en los que las barras tocan a id-rectángulos. En cada intervalo [ai , ai+1 ]
nos fijamos si v es adyacente a alguno de los vértices cuyas barras en φ se
encuentran en dicho intervalo. Si no es adyacente a ninguno de ellos abrimos
un id-rectángulo de anchura [ai , ai+1 ] sobre la barra de v (la primera vez que
ocurra esto, en vez de abrir un id-rectángulo eliminamos ese trozo con el fin de
convertir la circunferencia en una barra). Si es adyacente a k de ellos dividimos
el intervalo [ai , ai+1 ] en k +1 subintervalos de igual amplitud y para cada uno de
los k primeros abrimos id-rectángulos sobre todas las barras existentes excepto
sobre las correspondientes a v y a uno de ellos en cada caso. En el último
subintervalo abrimos un id-rectángulo sobre la barra correspondiente a v con el
fin de conservar las visibilidades existentes entre todas las demás barras.
Podemos, entonces, definir el bar-ı́ndice de un grafo G, que denotaremos
por bi(G), como el menor número n para el que G es bar-representable en una
superficie de género n. Hay que hacer notar que no partiremos del plano sino
que lo haremos del cilindro, por lo que diremos que un grafo tiene bar-ı́ndice 0
si es bar-cilı́ndrico.
Es necesario destacar el hecho de que no se trata de un género ya que puede
darse el caso de que el bar-ı́ndice de un grafo sea menor que el de un subgrafo
suyo. Ası́ por ejemplo, como se prueba en [3], el grafo de la Figura 6 tiene
bar-ı́ndice 0 por ser cilı́ndrico y 3-conexo y, sin embargo, posee un subgrafo
no conexo (dibujado en trazo grueso) cuyo bar-ı́ndice es mayor que 1 (no es
bar-tórico).
Sin más que hacer pequeñas modificaciones en la demostración de la Proposición 4 y teniendo en cuenta no sólo los extremos de las barras sino también
r
r
r
r
r
r
r
r
r
r
r
r
Figura 6: Un grafo bar-tórico con un subgrafo que no lo es.
los puntos en que éstas tocan a los id-rectángulos es fácil probar el siguiente
resultado.
Proposición 9. Es posible computar el esqueleto de una bar-representación en
On de un grafo de N vértices en tiempo O((N + n) log(N + n)).
Una primera relación existente entre el género g(G) (representación topológica) y el bar-ı́ndice bi(G) (representación de visibilidad) de un grafo G es la
que nos da el siguiente teorema.
Teorema 10. El bar-ı́ndice de un grafo es mayor o igual que su género.
Demostración: Dada una bar-representación en la superficie ortogonal estándar
de género n, podemos situar los vértices del grafo en el extremo izquierdo de
cada barra. Dado que las ventanas de visibilidad no se intersecan, podemos
trazar las aristas a través de dichas ventanas de visibilidad y llevarlas hasta los
vértices paralelamente a las barras correspondientes.
Es posible, sin embargo, encontrar ejemplos de grafos cuyo bar-ı́ndice es
estrictamente mayor que su género.
r
r
r
r
r
r
r
r
Figura 7: Un grafo cuyo bar-ı́ndice es mayor que su género.
En la Figura 7 podemos ver un grafo no conexo y tórico (g(G) = 1) que,
sin embargo, no es bar-tórico ya que un grafo no conexo y tórico es bar-tórico
si, y sólo si, es bar-cilı́ndrico (ver [3]) y la componente 1-conexa del grafo de la
Figura 7 no es bar-cilı́ndrica ya que su árbol de bloques-puntos-de-corte no es
una oruga (ver [8]). Como consecuencia de ello, podemos enunciar la siguiente
proposición.
Proposición 11. Existen grafos cuyo bar-ı́ndice es estrictamente mayor que su
género.
La magnitud del bar-ı́ndice de un grafo está relacionada con su grado de
conectividad. El siguiente teorema es una prueba de ello.
Teorema 12. El bar-ı́ndice de un grafo (n + 2)-conexo de género n es n.
Demostración: Realizaremos la demostración haciendo inducción en n.
Para n = 1 y dado que todo grafo tórico y 3-conexo es bar-tórico (ver [3])
el teorema es cierto.
Supongamos ahora que tenemos un grafo G (n + 2)-conexo de género n y
consideremos una inmersión suya en On . Deben existir, necesariamente, ciclos
en G que recorran a On en la dirección de los meridianos (en caso contrario
podrı́amos representar G en On−1 y su género no serı́a n). Cortando por dicho
ciclo y duplicando tanto sus vértices como sus aristas obtenemos un nuevo grafo
G0 (n + 1)-conexo (de no serlo es posible modificar el corte de forma que sı́ lo
sea) y de género menor que n. Podemos entonces, por hipótesis de inducción
encontrar una bar-representación de G0 que conserve la topologı́a, por lo que podemos identificar de nuevo las barras correspondientes a los vértices duplicados
para obtener, de esta forma, una bar-representación de G en On .
Teniendo en cuenta las relaciones entre el grado de conectividad de un grafo
y su género (ver [5]), podemos dar el siguiente resultado.
(n − 3)(n − 4)
.
Corolario 13. Para 3 ≤ n ≤ 16 se verifica que bi(Kn ) =
12
4
Conclusiones y Problemas abiertos
En el presente trabajo se ha probado que, haciendo uso de unos modelos adecuados de representación de superficies (las superficies ortogonales estándares),
es posible encontrar bar-representaciones de cualquier grafo sin más que elegir
un género adecuado para la superficie sobre la que se va a bar-representar.
Es obvio la cantidad de problemas abiertos que se nos plantean. Entre ellos
y quizás el más complejo sea el del estudio del bar-ı́ndice de un grafo que, al
igual que ocurre con su género (ver [9]), conjeturamos que es un problema de
naturaleza NP-completa.
Actualmente estamos trabajando en la determinación del bar-ı́ndice para
algunas familias destacadas de grafos, como son los planos, los completos y los
bipartitos completos.
Referencias
[1] N. L. Biggs, E. K. Lloyd y R. J. Wilson. Graph Theory 1736-1936. Clarendon Press, Oxford, 1976.
[2] G. Chartrand y F. Harary. Planar permutation graphs. Ann. Inst. H.
Poincaré, Sect B 3 pp. 433–438, 1967.
[3] F.J. Cobos, J.C. Dana, A. Márquez y F. Mateos. Representation of graphs
on a torus. 3rd International conference in Graph Theory. Bled (Eslovenia),
1995.
[4] M. Fréchet y Ky Fan. Initiation to Combinatorial Topology.
Prindle. Weber and Schmidt, 1967.
Boston:
[5] N. Hartsfield y G. Ringel. Pearls in Graph Theory: A Comprehensive
Introduction. Academic Press, Inc., 1990.
[6] R. Tamassia y I.G. Tollis. A unified approach to visibility representations of
planar graphs. Discrete and Computational Geometry, vol. 1, pp. 321–341,
1986.
[7] R. Tamassia y I.G. Tollis. Tessellation representations of planar graphs.
In Proc. 27th Annual Allerton Conf., pp. 48–57, University of Illinois at
Urbana-Champaign, 1989.
[8] R. Tamassia y I.G. Tollis. Representations of graphs on a cylinder. SIAM
J. Discrete Mathematics, vol. 4 No 1, pp. 139–149, February 1991.
[9] C. Thomassen. The Graph Genus Problem Is NP-Complete. Journal of
Algorithms, vol. 10, pp. 568–576, 1989.
[10] H. Whitney. Congruent graphs and the connectivity of graphs. Amer. J.
Math. 55, pp. 339–362, 1932.
[11] S. K. Wismath. Characterizing bar line-of-sight graphs. In Proc. ACM
Symp. on Computational Geometry, pp. 147–152, Baltimore. MD., 1985.