Apuntes De Cálculo Multivariable.

1
Apuntes De Cálculo Multivariable.
Prof. Henry Lázaro.
Departamento de Ciencias Básicas
Unidades Tecnológicas de Santander
uts
Departamento
DepartamentoDe
DeCiencias
CienciasBásicas
Básicas
Cálculo Multivariable
2014
2014
2
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
3
Contenido
Introducción. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1. Función Multivariable. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.1. Definición de Función Multivariable. . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
1.2. Función Polinómica y Racional
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
1.3. Graficas de una Función de Varias Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
1.4. Curvas de Nivel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
2. Límites y Continuidad de Funciones Multivariables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2.1. Métodos para el Cálculo de limites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 16
2.1.1. Método de sustitución . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
2.1.2. Método de las Trayectorias . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
2.1.3. Coordenadas Polares
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
2.2. Continuidad de una Función Multivariable
3.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
Derivadas Parciales de una Función Multivariable
3.1. Interpretación Geométrica de la Derivada
3.2. Derivadas Parciales de Orden superior
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
3.3. Regla de la cadena
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
3.4. Diagrama del Árbol
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
3.5. Derivada Implícita
. . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
3.6. Derivada Direccional
3.7. Vector Gradiente
. . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
3.8. Máximos y mínimos de una función Multivariable
3.8.1.Extremos Relativos
3.8.2.Puntos Críticos
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
3.9. Criterio de la segunda derivada
3.10. Multiplicadores de Langrage
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
4. Integración de Funciones Multivariables
4.1. Integrales Iteradas
4.2. Región tipo I y II
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
4.3. Momentos y centro de masa
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
4.4. Integrales dobles en Coordenadas Polares
4.5. Integrales Triples
. . . . . . . . . . . . . . . . . . . . . . . . . . . 39
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
4.6. Aplicaciones de las integrales triples
. . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
4.7. Integrales triples en otros sistemas de coordenados
4.7.1.Coordenadas Cilíndricas
. . . . . . . . . . . . . . . . . . . . . . . . . 42
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
4
4.7.2.Coordenadas Esféricas
5. Calculo Vectorial
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
5.1. Campo Vectorial
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
5.2. Integral de línea
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
5.3. Método de Evaluación
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
5.4. Teorema de Green
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
5.5. Teorema de Stokes
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
6. Bibliografía
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
5
INTRODUCCIÓN.
El Cálculo Multivariable es la rama de las matemáticas que nos ayuda hacer una
proyección del Cálculo Diferencial e Integral de funciones de una variable al estudio de
funciones de varias variables.
En esencia, el Cálculo Multivariable, se dedica al estudio de varias variables de modo
simultáneo. Es decir, tomando un objeto y no sólo medimos un aspecto suyo sino que
considera varios aspectos y tratamos de determinar la relación entre estas medidas. Es
decir medimos no solo una de sus características como el peso, la altura, el ancho,… sino
que buscamos la relación entre ellas; lo mismo ocurre con el análisis Multivariable de
funciones con múltiples incógnitas.
Con el desarrollo de la informática, se hace posible el desarrollo e implementación de
programas que ayudan con la construcción de gráficos en 3D haciendo más agradable y
motivante el análisis de esta clases de funciones y de esta manera podemos dar solución
a problemas donde el Cálculo Diferencial e Integral se limitado. Es por esto que podemos
con confianza decir que el Cálculo Multivariable, no es más que otra cosa que el Cálculo
Diferencial e Integral aplicado ya no solo a curvas planas en un plano cartesiano, sino el
trabajo con niveles que son las superficies descritas por las funciones de varias variables
y representadas en espacios de tres dimensiones.
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
6
FUNCIÓN DE VARIAS VARIABLES
Una función de una variable
número
de un dominio de
es una regla que asigna un número nuevo a cada
determinado; pero es de aclarar que estas funciones son
una idealización conveniente de un gran número de situaciones matemáticas o reales,
pero si queremos pensar en ejemplos de funciones que estén relacionadas con la
ingeniería, nos veremos tentados a ampliar este concepto de tal manera que incluya
magnitudes que dependan de más de una variable.
Cuando estudiamos la funciones con una variable siempre tomamos el conjunto de los
números reales como el dominio de dichas funciones, es decir trabajos con la recta
numérica para obtener una representación de la situación en el plano cartesiano; con
respecto a las funciones de más de una variable debemos tener en cuenta que no
vamos a trabajar sobre el plano cartesiano sino con el plano cartesiano; puesto que el
dominio de las funciones de más de una variables son el plano cartesiano
o un
subconjunto de él.
Algunos ejemplos comunes de esta clase de funciones son:
a. El área de un rectángulo:
b. El volumen de un cilindro circular:
c. El perímetro de un rectángulo:
d. El volumen del cono circular:
La definición formal de una función de varia variables es:
Una función de varias variables
es una regla de correspondencia que le
asigna a cada elemento del dominio de la forma
número
del conjunto de los números Reales
de
uno y solo un
.
El conjunto de los elementos
se llama DOMINO de la función y el conjunto de
los valores correspondientes a
recibe el nombre de RANGO. Para facilitar el
análisis de esta clase de funciones se trabajan con funciones de dos variables.
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
7
DEFINICION. 1
Una función de dos variables se puede
escribir mediante
𝑧
𝑓 𝑥 𝑦
y se lee
"𝑓 𝑑𝑒 𝑥 𝑑𝑒 𝑦" y se define como la regla de correspondencia que le asigna a cada
para ordenado de los números reales 𝑥 𝑦
El conjunto de pares ordenados
𝑥 𝑦
𝑅
un nuevo valor numérico 𝑧
se llaman
𝑅.
Dominio de la Función y su
representación gráfica es una región determina de 𝑅 o plano cartesiano 𝑥 y 𝑦 el
conjunto de los valores correspondientes a 𝑧
𝑓 𝑥 𝑦 que se lee "𝑓 𝑑𝑒 𝑧" se denomina
RANGO de la función. Las variables x, y, y se denominan variables independientes y 𝑧
es la variable dependiente.
En forma general podemos afirmar que toda función de dos variables tiene como dominio
un subconjunto de
y como rango o conjunto de imágenes un subconjunto de .
Ejemplo:
Hallar el domino, graficarlo y rango de cada una de las siguientes función
√
√
√
√
√
Solución:
√
Esta función está definida como la raíz cuadrada y para esto debemos tener en cuenta
que el valor del subradical debe ser mayor o igual a cero; por tal razón el dominio de la
función está dado por:
{
Departamento De Ciencias Básicas
⁄
}
Cálculo Multivariable
2014
8
Ahora el dominio de f consiste en todos los pares ordenados
que satisface la
condición:
es decir el dominio seria todos los puntos
que están sobre las rectas
además de todos los puntos por
encima y entre ellas como se muestra en la figura:
y=x
Y
y=-x
Dominio de la
función f
X
Por otro lado los valores de z correspondientes al resultado de la raíz cuadrada son
siempre positivos y mayores e iguales a cero, luego el rango está dado por:
{
⁄
}
√
Esta función está definida como el logaritmo natural de la raíz cuadrada de una función de
dos variables al cuadrado y para esto debemos tener en cuenta que el valor del subradical
debe ser estrictamente mayor que cero ya que el logaritmo de cero no existe; por tal razón
el dominio de la función está dado por:
{
}
⁄
La inecuación que hace parte del subradical:
√
corresponde a una
circunferencia con centro en el origen y radio uno y el dominio son todos los puntos que
se encuentran por fuera de la circunferencia y los puntos de la frontera de la
circunferencia no hacen parte del dominio porque allí la inecuación se hace igual a cero,
como se muestra en la figura:
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
9
El rango está dado por todos los valores de
mayores a cero, puesto que el logaritmo de
un número siempre es positivo y estrictamente mayor a cero, luego
{
}
⁄
√
Esta función está definida mediante un cociente, por lo tanto el denominador no puede ser
igual a cero y por otra parte el numerador como es una raíz cuadrada el subradical debe
ser mayor o igual a cero, luego:
⁄
{
}
La gráfica corresponde a todos los puntos del plano cartesiano por encima del eje x
excluyéndolo.
Y
Dominio de la función f
X
El rango está dado por todos los números reales R positivos, puesto que el denominador
puede ser un número positivo o negativo pero diferente de cero, mientras que el
numerador es positivo e igual a cero, luego:
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
10
√
La función está definida como una raíz cuadra por lo tanto el subradical debe ser positivo
e igual a cero; luego:
Para esto debemos analizar la gráfica de la función coseno,
es decir:
y
1
x
-1
Para la función coseno se observa que solo es positiva cuando el ángulo está
comprendido entre los valores:
f(x)=cos(x
Como nuestra función tiene un ángulo:
positiva; es decir:
entonces para que esta función sea
luego:
por consiguiente:
{
⁄
}
Ahora, la gráfica del dominio será los círculos concéntricos cuando:
Luego:
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
11
√
Esta función está compuesta por la suma de dos funciones y el domino de ella es la
intersección de los dominios de cada una de las funciones que la compone; es decir que
el dominio es el conjunto de puntos del plano que satisfacen las dos condiciones; luego el
dominio está dado por:
Así que:
{
⁄
}
Ahora la gráfica está dada por:
Si evaluamos las funciones en los pares ordenados del domino obtenemos que para la
raíz cuadrada siempre abra un resultado positivo y menores que √ y para el logaritmo
natural obtendremos valores estrictamente menores que
; ahora como
√
entonces:
⁄
{
(
√ }
√ )
FUNCIONES POLINOMIALES Y RACIONALES
Una Función Polinomial de dos variables consiste en la suma de potencias
donde
m y n son números enteros no negativos. El cociente de dos funciones Polinomiales se
denominan Función Racional.
Por ejemplo:
Funciones Polinomiales:
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
12
Funciones Racionales:
El dominio de una función Polinomial es el plano XY y el domino de una función racional
es el plano XY excepto aquellos pares ordenados
donde la sea igual a la porque
en esos puntos el denominador es igual a cero.
GRAFICA DE UNA FUNCIÓN DE VARIAS VARIABLES:
Sea f una función de dos variables, entonces la gráfica de f es el conjunto de puntos
para los cuales
y
; es decir la grafica de una función
de dos variables es una superficie tridimensional.
Ejemplo:
La grafica de la función:
La ecuación general de la esfera, donde A, B, C, D, E, F, G, H, I, J son constantes; está
dada por la ecuación:
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
13
Mediante esta ecuación podemos identificar las superficies cuadradas como:
ESFEROIDES, ELIPSOIDES, PARABOLOIDES, HIPERBOLOIDES, CONOS Y
CILINDROS.
ELIPSOIDE
La superficie es una esfera si
HIPERBOLE DE UN HOJA
El eje del hiperboloide corresponde
a la variable cuyo coeficiente es
negativo.
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
14
HIPERBOLE DE DOS HOJAS
El eje del hiperboloide corresponde
a la variable cuyo coeficiente es
positivo. No hay traza en el plano
perpendicular al eje.
CONO ELÍPTICO
El
eje
del
cono
elíptico
corresponde a la variable cuyo
coeficiente es negativo. La trazas
con los planos coordenado son
rectas que se cortan.
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
15
CURVAS DE NIVEL
Sea la función de dos variables
entonces las curvas de nivel se definen como:
donde c es constante que cumpla con la condición dada por la función f. Las curvas de
nivel es un método útil para describir una función de dos variables mediante la trazas en el plano
, trazas de la forma:
Ejemplo:
1. Trazar las curvas de nivel para la función
√
Solución
La ecuación general que describe la familia de curvas de nivel de la función está dada por:
√
estos valores se cumplen para
. Gráficamente se observa:
√
z
C=3
C=2.5
C=2
C=1.5
C=1
C=0.5
√
√
√
√
√
y
√
x
CURVAS DE NIVEL
2.
GRÁFICA DE LA FUNCIÓN
Trazar las curvas de nivel para la función
Solución
La ecuación general que describe la familia de curvas de nivel de la función está dada por
, donde
y esta familia de curvas son cilindros concéntricos de radio √ . Gráficamente
se observa:
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
16
LÍMITES Y CONTINUIDAD
LÍMITE Y CONTINUIDAD
La definición de límite está basada en la noción de proximidad y ya hemos visto que la noción de
límite y continuidad pueden ser extendidas a funciones entre dos espacios métricos y para esto
debemos definir la distancia entre dos puntos del espacio
; es decir:
Sean los puntos A
entonces la distancia
y el punto
que pertenecen a
dada por:
√
Para toda función de dos variables cuyo dominio incluye puntos arbitrariamente cercanos al punto
. Entonces decimos que el límite de la función
cuando
tiende a
es igual a
entonces se denota:
Si para todo número
hay un número correspondiente
siempre que
y
√
tal que |
|
.
El comportamiento de
en el punto
del dominio no es importante; es decir no
necesariamente de estar definida en dicho punto puesto que lo que nos interesa es que:
√
.
PROPIEDADES DE LOS LIMITES DE FUNCIONES DE DOS VARIABLES
Sean
y
funciones de dos variables y si:
Entonces:
[
]
[
]
[
]
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
17
√
√
√
MÉTODOS PARA EL CÁLCULO DE LOS LÍMITES
1. MÉTODO DE SUSTITUCIÓN:
Al igual que las funciones de una variable, los límites de una función de dos variables se pueden
determinar sustituyendo el valor de cada una de las variables.
Ejemplo:
Hallar cada uno de los siguientes límites si existen:
(
)
Solución
Sustituyendo el valor de las variables, tenemos que:
(
)
Luego
(
(
)
)
Solución
Sustituyendo el valor de las variables, tenemos que:
(
)
Como el resultado nos muestra una indeterminada, entonces empleando los casos de factorización
trataremos de simplificar la función para eliminar la indeterminada.
Luego
(
)
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
18
(
)
Solución
Sustituyendo el valor de las variables, tenemos que:
(
)
Empleando los casos de factorización trataremos de eliminar la indeterminada.
(
[
)
]
Luego
(
[
)
]
Solución
Sustituyendo el valor de las variables, tenemos que:
[
]
Luego
(
)
2. MÉTODO DE TRAYECTORIAS:
El límite de una función de una variable existe siempre y cuando el límite de la función cuando se
cerca al punto crítico por la izquierda sea igual a límite cuando se acerca por la derecha. Para la
definición del límite de una función de dos variables debemos tener en cuenta que en el plano no
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
19
vamos a encontrar dos caminos para llegar a un punto sino infinitos caminos; luego podemos decir
que si distintas trayectorias de acercamiento conducen a distintos valores L, afirmamos que el límite
no existe.
Gráficamente, ilustramos la anterior apreciación:
Se acercan a lo largo de la
recta vertical y horizontal
que pasa por (a, b)
Se acercan a lo largo
de toda curva que
pasa por (a, b)
Se acercan a lo largo de
todas las líneas rectas que
pasa por (a, b)
Tres de las muchas maneras de aproximarse al punto (a, b).
Ejemplo:
Hallar cada uno de los siguientes límites si existen:
(
)
Solución
Sustituyendo el valor de las variables, tenemos que:
(
)
Ahora no hay forma de quitar la indeterminada por medio de los procesos algebraicos, entonces
intentaremos determinar el límite por las trayectorias: A lo largo del eje x, es decir
; A lo
largo del eje y, es decir
, donde
; a lo largo de la recta
, a lo largo de las rectas
m es la pendiente de la recta que pasa por el punto (0, 0)
Entonces cuando
(
tenemos que:
)
(
)
(
)
(
)
Luego el limite a lo largo del eje x es igual a cero (0).
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
20
Entonces cuando
(
tenemos que:
)
(
)
(
)
(
)
Luego el limite a lo largo del eje y es igual a cero (0).
Entonces cuando
(
tenemos que:
)
(
)
(
)
Luego el limite a lo largo de la recta y = x es igual a .
Entonces cuando
(
tenemos que:
)
(
)
Luego el limite a lo largo de la recta y = x es igual a
(
)
.
Como se observa que los límites son diferentes concluimos que el LÍMITE NO EXISTE.
(
)
Solución
Sustituyendo el valor de las variables obtenemos una indeterminada que no se puede eliminar
mediante los procesos algebraicos.
Ahora determinamos el límite empleando las trayectorias y utilizaremos dos de ellas: A lo largo del
eje x; es decir tomando a
y a lo largo del eje y; es decir
(
)
(
)
(
)
(
)
Luego el límite de la función a lo largo del eje x está dado por:
(
Departamento De Ciencias Básicas
)
Cálculo Multivariable
2014
21
(
(
)
(
)
(
)
)
Luego el límite de la función a lo largo del eje y está dado por:
(
)
Como los dos límites son diferentes concluimos que el LÍMITE NO EXISTE
3. COORDENADAS POLARES:
En un sistema de coordenadas rectangulares o cartesiano se puede localizar un punto con una sola
pareja de puntos
estos valores son las distancias dirigidas, partiendo del origen, desde los
ejes x e y respectivamente. El origen es el punto donde se intersectan los dos ejes coordenados;
gráficamente tenemos que:
Todo punto del plano cartesiano
remplazando los valores de y,
se puede localizar en el plano de coordenadas polares
por:
En algunos límites de funciones de dos variables es adecuado usar coordenadas polares,
especialmente para límites que tienden al origen de coordenadas; es decir
solo si
√
si y
Así que, algunas veces, los límites para funciones de dos variables
pueden expresarse como límites que incluyen sólo una variable, que en este caso es:
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
22
Ejemplo:
Hallar los siguientes límites empleando las coordenadas polares:
[
]
Solución
Sustituyendo por las coordenadas polares, tenemos que:
[
]
[
]
Luego:
[(
[
)(
)]
]
Solución
Sustituyendo por las coordenadas polares, tenemos que:
[
[
]
[
]
[
[
]
]
]
[
]
Luego:
[
Departamento De Ciencias Básicas
]
Cálculo Multivariable
2014
23
CONTINUIDAD DE FUNCIONES MULTIVARIABLES
Se dice que la función de dos variables es continua en el punto
tres condiciones, que se plantean a continuación:
si y solo si cumple con las
1.
2.
3.
Si una función
no es continua en
se afirma que la función es discontinua. La gráfica
de una función de dos variables, es una superficie sin huecos; es decir que si
es continua en
una región R del plano XY entonces afirmamos que es continua para todo punto de la región R
del plano.
Ejemplo:
Determinar si la función
es continua en el punto crítico:
{
Solución
Primero calculamos el valor de
entonces; por definición de la función tenemos que:
Ahora el límite
Ahora podemos eliminar la indeterminada empleando los procesos algebraicos:
Como
entonces la función
{
es
continua en el punto
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
24
{
Solución
Primero calculamos el valor de
entonces; por definición de la función tenemos que:
Ahora el límite
Como
entonces la función
{
es continua en el punto
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
25
DERIVADAS PARCIALES DE UNA FUNCIÓN MULTIVARIABLE
En esta parte estudiaremos el comportamiento de algunas funciones mediante el cambio de una de
sus variables respecto a la otra; en esta unidad estudiaremos el concepto de derivada, sus principales
propiedades, el vector gradiente y sus propiedades y una variedad de ejemplos resueltos, y algunos
ejercicios propuestos.
Recordemos que la derivad de una función de una variable
está dada por el límite:
Exactamente de la misma manera, podemos definir las derivadas parciales de una función de dos
variables
con respecto a cada una de ellas. Para esto recordemos algunas reglas de las
derivadas de una función de una variable.
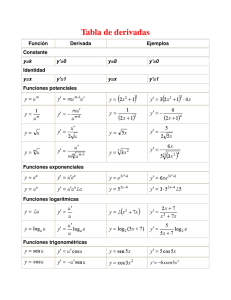
1.
2.
3.
4.

k   0
x   1
14. cos u   u  sin u

x   nx
kx   knx
15. tan u   u  sec u

16. cot u   u  csc u
n 1
n
n
6.
7.
u 
 nu
uv 
 u v  uv
8.
n


n 1
u

 u  u v  uv 
9.   
v2
v
10.
e   u e
u
a   a
u
u  ln a
 u
12. ln u  
u

13. sin u   u  cos u
11.
u
2

n.1
u  v  w  u   v  w
ku  ku 
5.
2
u
Departamento De Ciencias Básicas
17. sec u   u  sec u tan u

18. csc u   u  csc u c tan u

19. arcsin u  

20. arccos u  
21.
arctan u  
u
1 u2
 u
1 u2
u
1 u2
 u

22. arc cot u  
1 u2
u

23. arc sec u  
u u 2 1
 u

24. arc csc u  
u u 2 1
Cálculo Multivariable
2014
24
Definición
Sea
una función de dos variables, que en adelante simbolizaremos como:
entonces las derivadas parciales, es decir las derivadas respecto a cada una de las variables están dadas
por:
Derivada de la función respecto a la variable x:
Derivada de la función respecto a la variable y:
Siempre que el límite exista.
Ejemplo:
Hallar las derivadas parciales de cada una de las funciones dadas:
Solución
Derivada respecto a la variable x:
[
]
Luego
Derivada respecto a la variable y:
[
]
Luego
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
25
Solución:
Derivada respecto a la variable x:
[
]
Luego
Derivada respecto a la variable y:
[
]
Luego
Este mismo procedimiento, de calcular las derivadas parciales lo podemos hacer utilizando las reglas de
las derivadas de una variable teniendo en cuenta que “si derivas respecto a una de las variables las
otras variables se comportan como constante; es decir si derivas con respecto a la x la y se
comporta como una constante y viceversa, también hay que tener en cuenta que la derivada
de una constante es igual a cero”
Solución
Derivada respecto a la variable x:
Luego:
Derivada respecto a la variable y:
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
26
Luego:
Solución
Observamos que hay una función de tres variables, entonces; debemos derivadas por cada una de las
variables, es decir:
Derivada respecto a la variable x:
Luego:
Derivada respecto a la variable y:
Luego:
Derivada respecto a la variable z:
Luego:
√
Solución
Derivada respecto a la variable x:
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
27
(√
√
)
√
Luego:
(√
)
Derivada respecto a la variable y:
√
(√
)
√
Luego:
(√
)
( )
Solución
Derivada respecto a la variable x:
Derivada respecto a la variable y:
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
28
INTERPRETACION GEOMETRICA DE LA DERIVADA
Sea la función
que representa una superficie y el punto
otro lado el plano vertical
que intersecta la superficie
que intersecta la superficie
en la curva
donde
en la curva
por
y el plano
Tal y como se muestra en las figuras:
Entonces las derivadas parciales de la superficie; es decir
y evaluadas en el punto
representa la recta tangente a las curvas
y
dichas rectas se observan en la gráfica como
y
Por otra parte las derivadas parciales se pueden interpretar como la razón de cambio de la función
respecto a cada una de sus variables; es decir:
1. Si
entonces
representa la razón de cambio de
con respecto a
2. Si
entonces
representa la razón de cambio de
con respecto a
Ejemplo:
Hallar la ecuación de la recta tangente a la curva que se obtiene de la intersección del paraboloide
y el punto de la superficie
Solución
Como el punto de la superficie está dado por
se especifica el plano
mantiene constante el valor de x para todos los puntos en esa región.
Entonces calculemos la derivada parcial de
entonces se
con respecto a
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
29
Ahora del punto
se observa que
recta tangente a la curva que forma el plano
Si calculemos la derivada parcial de
entonces
y la superficie
es la pendiente de la
con respecto a
Ahora del punto
se observa que
recta tangente a la curva que forma el plano
entonces
y la superficie
es la pendiente de la
Ejemplo:
Hallar la ecuación de la recta tangente a la curva que se obtiene de la intersección del paraboloide
y el plano
cuando
Solución
Par poder hallar la pendiente de la recta tangente; calculamos la derivada y la evaluamos en el punto del
dominio formado por:
(
) es decir:
(
)
( )
Ahora el punto por el cual pasa la recta tangente está dada por:
(
)
( )
Recta tangente es:
(
Luego el punto de la superficie por donde pasa la
) entoces la recta tangente está dada por:
Gráficamente:
𝑧
𝑆𝑢𝑝𝑒𝑟𝑓𝑖𝑐𝑖𝑒 𝑧
𝑥
𝑦
𝑧
𝑥
𝑄(
Departamento De Ciencias Básicas
𝑥
)
Cálculo Multivariable
2014
30
DERIVADAS PARCIALES DE ORDEN SUPERIOR
Una función de dos variables
da lugar a dos derivadas parciales o derivadas de primer
orden. Estas son a su vez funciones de dos variables que puede ser derivada nuevamente para dar lugar a
las cuatro derivadas de segundo orden así:
1. Segunda derivada respecto a la variable ; es decir se deriva dos veces por la misma variable.
(
)
2. Segunda derivada primero respecto a la variable y después respecto a la variable
(
)
3. Segunda derivada primero respecto a la variable
(
después respecto a la variable
)
4. Segunda derivada respecto a la variable
(
; es decir se deriva dos veces por la misma variable.
)
Las derivadas
y
se conocen también con el nombre de derivadas cruzadas. Frecuentemente,
estas derivadas son iguales.
Ejemplo:
Hallar las derivadas parciales de segundo orden de la función, tenga en cuenta que:
Solución
Primera derivada respecto a la variable
Ahora segunda derivada de x respecto a x:
(
)
(
)
(
)
Ahora segunda derivada de x y después respecto a :
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
31
(
)
(
)
(
)
(
)
Primera derivada respecto a la variable
Ahora segunda derivada de
después respecto a x:
(
)
(
)
(
)
Segunda derivada de y respecto a la :
(
)
(
)
Ejemplo:
Hallar las derivadas parciales de segundo orden de la función:
(
)
Solución
Primera derivada respecto a la variable
(
)
(
)
Segundas derivadas:
(
)
(
)
(
)
(
)
(
(
(
)
)
(
)
(
)
)
(
)
Primera derivada respecto a la variable
(
)
(
)
Segundas derivadas:
(
( )
(
)
)
(
(
)
)
Departamento De Ciencias Básicas
(
(
)
)
(
(
)
)
(
)
Cálculo Multivariable
2014
32
REGLA DE LA CADENA.
La regla de la cadena es la propiedad que permite identificar la derivada de una función compuesta; es
decir que si tenemos la función f(x) y a su vez x es otra función u(x); entonces:
Esto ocurre para funciones de una variable. Ahora vemos para funciones de varias variables:
DEFINICIÓN:
Sea la función
una función de dos variables y diferenciable en
; además
y
funciones diferenciables en ; es decir
que a su vez es diferenciable en ,
luego:
Ejemplo:
para la función:
Calcular la derivada
teniendo en cuenta que
y
Solución:
entonces:
Si tenemos en cuenta que:
Ejemplo:
Calcular la derivada
y
para la función:
teniendo en cuenta que
y
Solución:
Ahora proyectando la formula
Departamento De Ciencias Básicas
a las variables
y
tenemos que:
Cálculo Multivariable
2014
33
Entonces:
[
]
[
]
[
]
[
]
DIAGRAMA DEL ÁRBOL
El diagrama del árbol es una forma gráfica de visualizar la relación entre las variables que
posee una función compuesta. Es decir si la función
de dos variables y las variables
y son funciones que poseen variables y entonces el diagrama del árbol está dado por:
Ahora para una función de tres variables, el diagrama del árbol quedara:
Ejemplo:
Construya el diagrama del árbol del siguiente caso:
Departamento De Ciencias Básicas
donde
Cálculo Multivariable
2014
34
Solución:
Del ejercicio se observa que la función f depende de los valores de
de
y depende de
entonces:
y
y a su vez
depende
Luego la regla de la cadena nos quedara:
DERIVADA IMPLICITA
Sea la función
una función de dos variables, tal que
a como una función
implícita de ; es decir
y que
y si suponemos que
sea
diferenciable. Entonces; aplicado la regla de la cadena; tenemos que:
Sustituyendo
Despejando
entonces:
tenemos que:
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
35
Ahora, si es una función de tres variables, la derivada implícita está dada por:
Ejemplo:
definir a
Sea la ecuación
es decir calculando:
implícitamente como una función de
y ;
y
Solución:
Calculamos
por lo que tomamos a
(
como una constante, entonces:
)
despejando la derivada
Ahora, tenemos que:
implícita; tenemos que:
Calculamos
(
por lo que tomamos a
como una constante, entonces:
)
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
36
despejando la derivada implícita;
Ahora, tenemos que:
tenemos que:
por lo que tomamos a
Calculamos
(
como una constante, entonces:
)
Ahora, tenemos que:
despejando la derivada implícita;
tenemos que:
DERIVADA DIRECCIONAL.
Sea
una función de dos variables y
vector unitario. Se llama Derivada Direccional de
Departamento De Ciencias Básicas
en el punto
con
en la dirección
un
a la derivada:
Cálculo Multivariable
2014
37
VECTOR GRADIENTE.
al vector cuyas componentes son las derivadas parciales; es
Se llama Gradiente de una función
decir:
(
)
Usando el gradiente, la derivada direccional se puede calcular mediante el producto escalar:
en el punto
La derivada direccional y el vector gradiente para una función de tres variables
en la dirección del vector unitario
son:
Y el vector gradiente está dado por:
(
)
Ejemplo:
Determine la derivada direccional de la función
en el punto
dirección del vector unitario cuyo ángulo con la parte positiva del eje x es
en la
.
Solución:
Las derivadas parciales están dadas por:
Ahora, el vector gradiente está dado por:
Para el punto
Ahora como
el gradiente tiene un valor de:
nuestro vector unitario será igual a
Departamento De Ciencias Básicas
entonces:
Cálculo Multivariable
2014
38
√
Por lo tanto la derivada direccional está dada por:
√
(
)
√
PLANO TANGENTE.
Sea
un punto sobre la superficie de nivel
donde el gradiente en dicho
punto está dado por
diferente de cero; es decir:
El plano tangente en
es aquel plano que pasa por el punto P y que es perpendicular a
Plano Tangente en
(x0, y0, z0)
Ejemplo:
Encuentre la curva de nivel
dicho punto (Dennis G. Zill (2011). Pág. 725)
en el punto
Grafique el gradiente en
Solución:
Como
se determina mediante:
entonces el valor para el punto
Luego la curva de nivel está dada por
Ahora el gradiente está dado por:
Departamento De Ciencias Básicas
por lo tanto
Cálculo Multivariable
2014
39
La grafica es:
𝟔𝒋
𝛁𝒇 𝟐 𝟑
𝟒𝒊
𝟔𝒋
𝟒𝒊
A = (2,3)
MÁXIMOS Y MÍNIMOS PARA FUNCIONES DE VARIAS VARIABLES
Para una función de una variable,
se puede determinar los valores máximos y mínimos
mediante el comportamiento de la primera y segunda deriva, a este estudio se le denomina
CRITERIO DE LA SEGUNDA DERIVADA. Para las funciones de varias variables este criterio es
viable por lo que trataremos de extender dicho criterio al caso de funciones de dos variables.
Empezamos por definir los puntos extremos relativos o locales para funciones de variables
y
EXTREMOS RELATIVOS:
Sea una función de dos variables se dice que el punto
alguna de estas condiciones.
es un extremo relativo si cumple con
i. Un número
es un MÁXIMO RELATIVO de una función
para todo
en algún disco abierto que contengo
.
si
ii. Un número
es un MÍNIMO RELATIVO de una función
para todo
en algún disco abierto que contengo
.
si
TEOREMA. (Condiciones necesarias de extremo relativo)
Sea una función de dos variables definida en un conjunto abierto
y
. Si es
diferenciable en el punto
y alcanza un máximo o un mínimo relativo en dicho punto se
verifica que:
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
40
PUNTOS CRITICOS.
Un PUNTO CRÍTICO de una función
es un punto
en el dominio de para el
cual
y
o si una de sus derivadas parciales no existe en el punto.
Para conocer si los puntos críticos de una función diferenciable corresponden a un máximo o a un
mínimo o a ninguna de las cosas, se puede utilizar el criterio de la segunda deriva.
CRITERIO DE LA SEGUNDA DERIVADA.
Sea
un punto crítico de
cerrado en
. Considerando que:
y suponga que
y
[
i.
ii.
iii.
iv.
Si
Si
Si
Si
continua en un disco
]
y
, entonces
es un Mínimo Relativo.
y
, entonces
es un Máximo Relativo.
, entonces
es un punto de silla.
, entonces el criterio no puede afirmar nada.
Ejemplo:
Encuentre los puntos críticos para
Solución:
Hallamos las derivadas parciales d primer orden están dadas por:
y
Como
Como
y
entonces:
por lo tanto existen cuatro puntos críticos:
y
Ejemplo:
Determinar los máximos y mínimos para
Solución:
En primer lugar hallamos las derivadas parciales de primer orden:
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
41
y
Como
y
Ahora remplazando
entonces:
en la ecuación
tenemos que:
( )
Remplazando
en
críticos son:
entonces
por lo tanto los puntos
y
Ahora podemos aplicar el criterio de la segunda derivada, entonces:
[
 Para el primer punto
tenemos que:
[
Como:
]
y
es un Punto de silla.
 Para el primer punto
tenemos que:
[
Como:
]
y
 Para el primer punto
es un Punto de silla.
tenemos que:
[
Como:
y
 Para el primer punto
]
]
es un Punto Mínimo Relativo.
tenemos que:
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
42
[
Como:
y
]
es un Punto Máximo Relativo.
MULTIPLICADORES DE LAGRANGE
El método de Multiplicadores de LaGrange para calcular el valor máximo o el valor mínimo de
una función con restricciones. Por lo tanto llamaremos al extremo condicionado de una función
, al valor máximo o mínimo de esta función alcanzado con la condición de que sus variables
están ligadas entre sí por la ecuación:
Ahora para calcular el extremo condicionado
de la función
con esta condición; trabajaremos con la función de LaGrange:
Donde
es el multiplicador de LaGrange y se buscan los extremos de
.
Las condiciones necesarias para que haya un extremo se reducen al sistema de las siguientes tres
ecuaciones:
Con las cuales podemos calcular los valores de las variables
y,
punto hay un extremo, se muestra de
para el máximo y
en cuenta que:
Para probar que en este
para el mínimo; teniendo
Ejemplo:
Determinar los extremos de la función
con la condición de que
Solución:
Aplicando la función de LaGrange, tenemos:
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
43
Ahora calculando las ecuaciones de restricción, tenemos que:
De estas ecuaciones aparece el sistema de ecuaciones lineales:
Si resolvemos dicho sistema obtenemos el punto
máximo o un valor mínimo, tenemos que:
, y,
Como
entonces el valor máximo es:
valor máximo de la función con la restricción es
Para determinar si es un valor
entonces el
.
Ejemplo:
Hallar el valor máximo y el valor mínimo de
intersección de
sobre la curva de
y,
Solución:
Como la función presenta tres variables y dos restricciones, entonces:
Ahora hallamos las ecuaciones de restricción:
;
;
Departamento De Ciencias Básicas
;
Cálculo Multivariable
2014
44
Aparece el sistema de ecuaciones lineales:
Resolviendo dicho sistema tenemos que:
y
obtenemos los puntos para el análisis
cuando
y el punto
cuando
Probemos estos datos para identificar cuál de ellos es un máximo o un mínimo:
Luego: Para
cuando
tenemos que:
( )
Como
entonces en el punto
(
hay un mínimo y su valor es:
)
Para (
) cuando
tenemos que:
(
Como
(
( )
entonces en el punto
)
)
(
)
hay un máximo y su valor es:
(
Departamento De Ciencias Básicas
)
Cálculo Multivariable
2014
45
INTEGRACIÓN DE UNA FUNCIÓN MULTIVARIABLE
El concepto de la integral definida de una función de una sola variable se puede ampliar a una
función de varias variables. La integral de una función de una variable recibe el nombre de integral
simple para poder distinguirla de un integral múltiple la cual incluye una función de varias
variables.
INTEGRAL ITERADAS.
Sea una función de dos variables definidas sobre una región cerrada
Integral Iterada Doble de sobre , denotada por:
∬
del plano
. Entonces la
∫ ∫
PROPIEDADES DE LAS INTEGRALES MULTIPLES
Sean f y g funciones de dos variables que son integrables sobre una región R del plan XY.
Entonces:
∬
∬
∬[
]
∬
∬
∬
∬
∬
∬
∬
REGIONES DE TIPO I Y II
Antes de continuar necesitamos examinar algunas regiones R especiales en el plano
.
REGIÓN TIPO I
La región R que se muestra en la figura es de tipo I ya que:
Donde las funciones
y
son continuasen la región R. Las integrales cumplen con:
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
46
∫ ∫
∫ [∫
]
REGIÓN TIPO II
La región R que se muestra en la figura es de tipo II ya que:
Donde las funciones
son continuasen la región R: Las integrales cumplen con:
∫ ∫
∫ [∫
]
Ejemplo:
Evalué la integral iterada de
sobre la región que se muestra en la figura:
Solución:
Según la gráfica la región es de tipo I, entonces la integral esta dad por:
∫ ∫
∫ [∫
]
∫
Departamento De Ciencias Básicas
[
]
∫
[
]
Cálculo Multivariable
2014
47
∫
[
]
∫
[
Luego el área de la región R es igual a
]
unidades cuadradas.
Ejemplo:
Evalué la integral iterada
∫ ∫
Solución:
Por la forma de la integral observamos que es una integral de tipo II entonces su grafica seria:
Ahora nuestra integral será:
∫ ∫
∫ [∫
∫ [
]
]
∫
∫
]
[
]
Luego:
∫ ∫
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
48
Nota: La Integral:
∫
∫
Esta última integral ∫
∫
∫
se resuelve por pates.
CENTRO DE MASA Y MOMENTOS.
Suponga que una lámina ocupa una región del plano
y que su densidad viene dada por la
función continua
para todo
en . Se define la masa de la lámina mediante la integral
doble:
∬
Los Momentos de la lámina respecto del eje
integrales dadas por:
y el eje
respectivamente, se definen mediante las
∬
∬
Por otro lado; las coordenadas del centro de masa de la lámina vienen dadas por:
̅ ̅
(
)
El centro de masa es el punto donde consideramos que se concentra toda la masa de la lámina. Si
es una constante, se dice que la lámina será homogénea y su centro de masa recibe el
nombre de centroide de la lámina
Ejemplo:
Hallar el centro de masa de una lámina triangular con vértices
si la función de
densidad es
Solución:
Como la cantidad de masa está dada por:
∫ ∫
Ahora, las coordenadas del centro de masa están dadas por:
∫ ∫
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
49
∫ ∫
(
Luego: Centro de Masa:
)
(
)
MOMENTO DE INERCIA:
El momento de inercia (también llamado segundo momento) de una partícula de masa
de un eje se define como
, donde
alrededor
es la distancia de la partícula al eje. El momento de
inercia de un cuerpo es considerado como una medida de la resistencia al girar cuando actúa en él
una fuerza de rotación. En particular si el eje de giro es el eje
inercia respecto al eje
o el eje
o el eje
entonces el momento de
es respectivamente:
∬
∬
La suma de estos dos momentos se llama Momento Polar de Inercia y se denota como
tiene que:
. Asi se
∬
Ejemplo:
Una lámina tiene la forma de la región limitada por
Calcular los momentos
y
y su densidad es
.
Solución:
Los momentos de inercias están dados por:
∫ ∫
∫ ∫
∫ ∫
Como:
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
50
INTEGRALES DOBLE EN COORDENADAS POLARES.
Algunas integrales dobles al calcularlas se nos hacen más fácil cuando empleamos las coordenadas
polares que las coordenadas rectangulares; en especial cuando contamos con regiones circulares; es
decir cuando aparecen integrandos de la forma:
Como sabemos la relación entre las coordenadas polares y las coordenadas cartesianas están dadas
por:
Es decir; sea
la región constituida por todos los puntos
que satisfacen
las condiciones
[
Si
] y es una función continua en la región
∬
La región
y
so funciones continuas en
entonces:
∫ ∫
debe cumplir con alguna de las siguientes graficas tanto para
como para
Ejemplo:
Evaluar la integral doble: ∬
por los círculos
donde
es la región en el semiplano superior acotado
y
Solución:
La región R se puede describir como:
gráficamente se puede observar que:
{
Departamento De Ciencias Básicas
⁄
}
Cálculo Multivariable
2014
51
Es la mitad del anillo mostrado en la figura que en coordenadas polares esta dad por:
Por lo tanto la integral es igual a:
∬
y
∫ ∫
∫ ∫
∫ [
∫ ∫
]
∫
∫ [
]
[
]
Libro Stewart 6 edición.
Ejemplo:
Use las coordenadas polares:
√
∫ ∫
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
52
Solución:
De los límites de las integrales podemos identificar la región
√
y
de la siguiente forma:
entonces la gráfica de la región es:
√
En consecuencia, las coordenadas polares están dadas por:
y
entonces la
integral se convierte en:
√
∫ ∫
∫
⁄
√
∫
∫
⁄
∫
⁄
⁄
]√
⁄
√
∫
⁄
∫
⁄
(
)
⁄
Dennis G. Zill (2011).
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
53
Ejemplo:
√
Encuentre el volumen del sólido que está bajo el hemisferio
y sobre la región
acotada por la gráfica de la circunferencia
Solución:
De la gráfica tenemos que:
∬√
En coordenadas polares las ecuaciones del hemisferio y la circunferencia se vuelven,
respectivamente:
∬√
∫
⁄
[
√
y
∫
⁄
ahora, usando simetría tenemos que:
∫
∫
∫
]
⁄
[
]
⁄
[
∫
]
⁄
[
]
⁄
(
)]
Dennis G. Zill (2011).
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
54
INTEGRALES TRPLES.
Sea una función de tres variables y continua en una región cerrada
del espacio tridimensional;
entonces la integral triple de la función sobre la región que se denota y se define como:
∭
∫ ∫ ∫
indica cómo se realiza la integral como en el caso de las integrales
dobles, se cumple el teorema de Fubini si f es continua; en otras palabras, una integral triple
se puede reducir a una triple integral iterada.
El orden de
La idea de considerar regiones acotadas
se clasifica en los siguientes tipos de regiones:
tal que
entonces la región
Región tipo I: La región de tipo I está delimitada por:
y
Es decir la integral está dada por:
∭
∫ ∫
∫
Región tipo II: La región de tipo I está delimitada por:
y
Es decir la integral está dada por:
∭
∫ ∫
∫
Región tipo III: La región de tipo I está delimitada por:
y
Es decir la integral está dada por:
∭
∫ ∫
∫
APLICACIONES DE LAS INTEGRALES TRIPLES.
A continuación relacionamos algunas aplicaciones prácticas de las integrales triples:
VOLUMEN:
Sea la función
definida en el solido
entonces el volumen esta dado por:
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
55
∭
MASA:
Sea la función
que representa la densidad entonces la masa del solido está dada por:
∭
PRIMEROS MOMENTOS Y CENTRO DE MASA.
Los primeros momentos del sólido alrededor de los planos están dados por las siguientes integrales:
∭
∭
Ahora, el centro de masa del sólido
∭
está dado por:
̅ ̅ ̅
(
)
SEGUNDOS MOMENTOS.
Los Segundos momentos son también conocidos como momentos de inercia de
ejes de coordenadas que se muestran en las siguientes integrales:
∭
alrededor de los
∭
∭
Ejemplo:
Evaluar la integral iterada indicada:
∫ ∫
∫
Solución:
∫ ∫
∫
∫ ∫
]
Departamento De Ciencias Básicas
∫ ∫
Cálculo Multivariable
2014
56
∫ (
∫ (
)]
∫ (
)
[
)
]
Ejemplo:
Encuentre el volumen del sólido en el primer cuadrante acotado por las gráficas de
y
,
(Dennis G. Zill (2011). Pág. 779)
Solución:
Gráficamente tenemos que:
Como se indica en la figura la primera integral es con respecto a
las otras están dadas por:
∫ ∫ ∫
[
∫ [
∫ ∫
⁄
⁄
]
]
⁄
y sus límites son:
∫ (
a
y
)
.
INTEGRALES TRIPLES EN OTROS SISTEMAS DE COORDENADAS.
Al igual que con las integrales dobles, en ocasiones un cambio de coordenadas puede facilitar la
resolución de un integral triple.
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
57
Un cambio de coordenadas cartesianas
biyectiva entre dos regiones
y
de
a otras coordenadas
es una aplicación
.
COORDENADAS CILINDRICAS.
Sea el punto de coordenadas
del espacio, en coordenadas cilíndricas está dado por:
como se muestra en la gráfica:
De la gráfica también vemos que las coordenadas rectangulares
coordenadas cilíndricas
de un punto se obtienen las
mediante las ecuaciones:
Por otra parte tenemos que:
Entonces, si
es una función continua sobre la región , la integral triple de dicha función
en la región R está dada por:
∭
∭
Departamento De Ciencias Básicas
∫ ∫
∫
Cálculo Multivariable
2014
58
COORDENADAS ESFERICAS.
Sea el punto de coordenadas
del espacio, en coordenadas cilíndricas está dado por:
como se muestra en la gráfica:
De la gráfica también vemos que las coordenadas rectangulares
coordenadas esféricas
mediante las ecuaciones:
de un punto se obtienen las
Por otra parte tenemos que:
Por consiguiente, una integral triple común en coordenadas esféricas tiene la forma:
∭
∭
∫ ∫
∫
Ejemplo:
Un sólido en el primer octante tiene la forma determinada por la gráfica del cono de un solo manto
√
está dada por
y los planos
y
Determinar el centro de masa si la densidad
(Dennis G. Zill (2011). Pág. 785)
Solución:
Como
entonces
√
Departamento De Ciencias Básicas
√
Gráficamente tenemos que:
Cálculo Multivariable
2014
59
Ahora el centro de masa está dado por:
∭
De la gráfica, podemos identificar los límites de cada una de las integrales; es decir:
⁄
∭
⁄
∫
∫ ∫
∫
⁄
∫
⁄
∫
∫
∫
⁄
]
∫
⁄
∫
(
∫
)]
⁄
∫
⁄
∫ ∫
∫
⁄
⁄
∫
]
∫
⁄
∫
∫
Ahora, empleando:
y
∫
∫
⁄
(
]
∫
)]
]
⁄
, tenemos también que:
⁄
∭
]
∫
⁄
∫
⁄
∭
∫
⁄
∫ ∫
⁄
∫ ∫
Departamento De Ciencias Básicas
∫
∫
]
Cálculo Multivariable
2014
60
⁄
∫
∫
⁄
⁄
⁄
∫
(
∫
)]
]
⁄
(
]
)
⁄
∭
∫
⁄
∫ ∫
∫
∫
]
⁄
∫
∫
⁄
∫
⁄
⁄
(
∫
)]
]
⁄
]
(
)
Como el centro de masa está dado por:
(
) entonces; tenemos que:
Por lo tanto, el centro de masa tiene las coordenadas aproximadas de:
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
61
Ejemplo:
Hallar el centro de masa de la región sólida
de densidad uniforme, limitada o acotada
inferiormente por la hoja superior del cono
y superiormente por la esfera
(Larson R (2006). Pág. 1039)
Solución:
entonces
En coordenadas esféricas, la ecuación de la esfera es:
Ahora la esfera y el cono se intersectan en:
y
Remplazando tenemos que:
entonces
√
entonces:
( ) remplazando
despejando el ángulo tenemos que
Ahora como
.
tenemos que:
√
( )
(
)
(
√
)
donde
Por consiguiente se puede utilizar el orden de integración
;
. Entonces el volumen es:
∫
∫
∫
⁄
∫
∫
|
⁄
∫
(
√
∫
)
Departamento De Ciencias Básicas
⁄
|
∫
(
√
)∫
(
⁄
√ )
Cálculo Multivariable
2014
62
CALCULO VECTORIAL.
Hasta este momento hemos estudiado, en el cálculo de tres tipos de integrales como son las
integrales definidas, las integrales dobles y triples; en este capítulo estudiaremos dos tipos de
integrales como son las integrales de línea y las integrales de superficie y el estudio de estos dos
conceptos dependen directamente de métodos vectoriales, que a su vez están relacionados con un
con las funciones vectoriales.
CAMPO VECTORIAL
En forma general un campo vectorial es una función cuyo dominio es un conjunto de puntos de
o,
y el rango esta determinar mediante un conjunto de vectores; es decir:
Sea
un conjunto de puntos de
que asigna a cada punto
, una región plana. Un campo vectorial sobre
en
es un función
un vector bidimensional
La mejor manera de representar un campo vectorial es dibujar la flecha que representa al vector
que inicia en el punto
. Como
es un vector bidimensional entonces se puede
expresar en términos de sus componentes; es decir:
Para facilitar nuestro trabajo con las componentes; remplazaremos a
entonces:
por
⟨
Para
y
por
⟩
el campo vectorial es de la forma:
⟨
⟩
INTEGRALES DE LÍNEA
Sea la curva
definida en el intervalo [
]y
diferenciable,
con su derivada es no nula en dicho intervalo (Por lo tanto afirmamos que la curva es suave en
dicho intervalo). Luego denotamos a la curva con
como .
Sea una función de dos variables y definida en una región del plano que contiene una curva
entonces la integral de línea se define como:
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
63
i.
La integral de línea de f con respecto a x a lo largo de C de A hasta B es:
∫
ii.
‖ ‖
La integral de línea de f con respecto a y a lo largo de C de A hasta B es:
∫
iii.
∑
‖ ‖
∑
La integral de línea de f con respecto a la longitud s a lo largo de C de A hasta B es:
∫
‖ ‖
∑
Para comprender mejor la definición de la integral de línea debemos tener en cuenta que el punto
sobre el subarco está dado por:
Punto de muestra sobre el arco K - ésimo
MÉTODO DE EVALUACIÓN: C definida por
función explícita
y
es posible utilizar
√
[
]
Si la curva C está definida por una
como un parámetro. Con
las integrales de línea señaladas anteriormente se
transforman en:
∫
∫
∫
∫
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
64
∫
[
√
∫
]
Una integral de línea a lo largo de una curva C suave por partes se define como la suma de las
integrales sobre las distintas curvas suaves cuya unión compone a C. Es decir:
∫
∫
∫
En muchas aplicaciones, las integrales de línea aparecen como una suma, es decir:
∫
∫
Es común escribir esta suma sin el segundo símbolo de integral, es decir:
∫
∫
∫
O simplemente:
∫
∫
∫
(Dennis G. Zill (2011). Pág. 804)
Ejemplo:
Evalué cada una de las integrales dadas sobre el cuarto de círculo C definido por
como se indica en la figura: (Dennis G. Zill (2011). Pág. 803)
∫
∫
∫
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
65
Solución:
∫
∫
⁄
∫
∫
⁄
⏞
⏞
⏞
⁄
⁄
[
∫
]
∫
∫
⁄
⁄
⏞
⏞
[
∫
⁄
⏞
∫
⁄
⁄
⁄
∫
∫
∫
⁄
∫
⁄
]
⏞
⏞
[
]
⏞
(√
)
⁄
Ejemplo:
Evalué la integral indicada, sobre la curva dada por
(2011). Pág. 805)
donde
(Dennis G. Zill
Solución:
En primer lugar construimos la curva C, es decir:
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
66
La curva C se define mediante la función explícita
como parámetro. Con
se deduce que:
∫ [
∫
Por consiguiente, podemos usar
]
∫
]
TEOREMA DE GREEN
Suponga que
es una curva cerrada simple suave por partes con una orientación positiva que limita
una región simplemente conexa . Si
∫
son continuas sobre , entonces:
∬(
)
Ejemplo:
Evalúe la integral cerrada ∮
donde C está definida como la frontera de
la región en el primer cuadrante que está acotada por las gráficas de
y
Solución:
Como el teorema de Green afirma que
∫
Entonces:
luego:
Por otro
lado la gráfica que corresponde a:
Ahora:
∮
Departamento De Ciencias Básicas
∬
Cálculo Multivariable
2014
67
∬
∫ ∫
]
∫
∫
Luego:
∮
TEOREMA DE STOKES
Sea una superficie orientada suave por partes acotada por una curva
partes. Sea:
cerrada simple suave por
Un campo vectorial para el cual
y
son continuas y tienen primeras derivadas parciales
continuas en una región abierta del espacio tridimensional que contiene a . Si se recorre en a
dirección positiva, entonces:
∮
Donde n es una normal unitaria a
∮
∬
en la dirección de la orientación de .
Ejemplo:
Sea la parte del cilindro
para el campo vectorial
para
Verifique el teorema de Stokes
Suponga que
se orienta hacia arriba.
Solución:
La superficie
la curva
se ilustra en la gráfica:
(la cual está compuesta por la unión de
Departamento De Ciencias Básicas
) y la región
Cálculo Multivariable
2014
68
La INTEGRAL DE SUPERFICIE para la función:
Estada por:
|
|
En este caso,
define el cilindro, la normal es
|
|
√
Por lo tanto
∬
∬
√
Para evaluar la última integral de superficie usamos ∮
entonces:
∬
∮
∬
∬
√
∫ ∫
∫ [
]
∫
La INTEGRAL DE LÍNEA la integral de línea es: ∮
Como
Sobre
es suave por partes, escribimos ∮
∫
∫
∮
∫
∫
por lo tanto
∫
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
69
Sobre
, por lo tanto
∫
∫
Sobre
, por lo tanto
∫
Sobre
∫
, por lo tanto
∫
∫
En consecuencia,
∮
Por lo tanto se comprueba el Teorema de Stokes cuando comparamos la integral de superficie y la
integral de línea.
Departamento De Ciencias Básicas
Cálculo Multivariable
2014
70
BIBLIOGRAFIA
 Dennis G. Zill (2011). Cálculo. Trascendentes Tempranas. 4a Edición.
 Stewart J (2008). Cálculo. Trascendentes Tempranas. 6a Edición.
 Leithold L. (1998). Cálculo con Geometría Analítica. 7a Edición.
 Larson P. (2006). Cálculo de Varias Variables. 8a Edición.

http://www.tec-digital.itcr.ac.cr/revistamatematica/cursos-linea/SUPERIOR/t3DerivadaParcial/node2.html

http://www.dma.fi.upm.es/mreye/calculo/guia/calculo_9_1_2.pdf

http://www.dma.fi.upm.es/mreyes/calculo/guia/calculo_9_1_3.pdf

http://www.dma.fi.upm.es/mreyes/calculo/guia/calculo_9_1_3.pdf

http://www.tec-digital.itcr.ac.cr/revistamatematica/cursos-linea/SUPERIOR/t6PlanoTangente/index.html. Grafica del plano tangente

http://es.scribd.com/doc/97627741/44/Multiplicadores-de-Lagrange

http://www.bdigital.unal.edu.co/3383/1/bernardoacevedofrias.2003.pdf.

http://mai19ucv.com.ve/Guias%20y%20Parciales/TEMA%203.pdf.

http://www.uantof.cl/facultades/csbasicas/Matematicas/academicos/emartinez/calculo3/line
a/linea.html Integral de línea
Departamento De Ciencias Básicas
Cálculo Multivariable
2014