sol logica combinacional

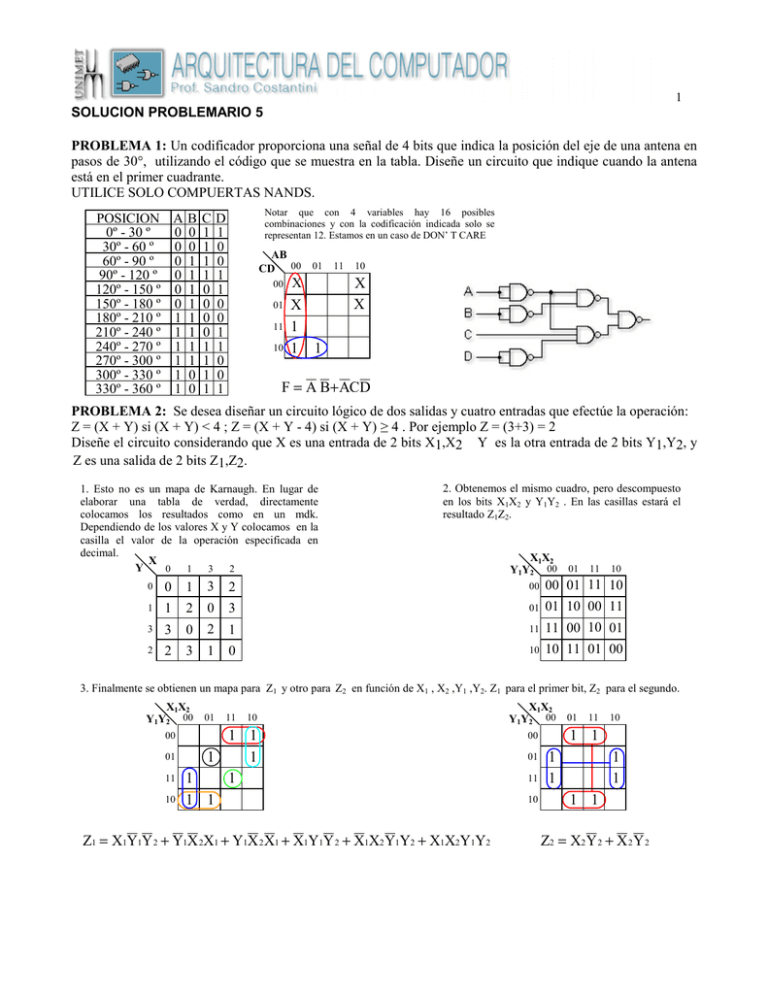
1
SOLUCION PROBLEMARIO 5
PROBLEMA 1: Un codificador proporciona una señal de 4 bits que indica la posición del eje de una antena en
pasos de 30°, utilizando el código que se muestra en la tabla. Diseñe un circuito que indique cuando la antena
está en el primer cuadrante.
UTILICE SOLO COMPUERTAS NANDS.
Notar que con 4 variables hay 16 posibles
combinaciones y con la codificación indicada solo se
representan 12. Estamos en un caso de DON’ T CARE
POSICION A B C D
0º - 30 º
0 0 1 1
30º - 60 º
0 0 1 0
60º - 90 º
0 1 1 0
90º - 120 º 0 1 1 1
120º - 150 º 0 1 0 1
150º - 180 º 0 1 0 0
180º - 210 º 1 1 0 0
210º - 240 º 1 1 0 1
240º - 270 º 1 1 1 1
270º - 300 º 1 1 1 0
300º - 330 º 1 0 1 0
330º - 360 º 1 0 1 1
AB
CD 00 01 11 10
00
X
01
X
1
1 1
11
10
X
X
F = A B+ ACD
PROBLEMA 2: Se desea diseñar un circuito lógico de dos salidas y cuatro entradas que efectúe la operación:
Z = (X + Y) si (X + Y) < 4 ; Z = (X + Y - 4) si (X + Y) ≥ 4 . Por ejemplo Z = (3+3) = 2
Diseñe el circuito considerando que X es una entrada de 2 bits X1,X2 Y es la otra entrada de 2 bits Y1,Y2, y
Z es una salida de 2 bits Z1,Z2.
1. Esto no es un mapa de Karnaugh. En lugar de
elaborar una tabla de verdad, directamente
colocamos los resultados como en un mdk.
Dependiendo de los valores X y Y colocamos en la
casilla el valor de la operación especificada en
decimal.
X
Y
0
1
3
2
2. Obtenemos el mismo cuadro, pero descompuesto
en los bits X1X2 y Y1Y2 . En las casillas estará el
resultado Z1Z2.
X1X2
Y1Y2 00 01 11 10
0
0
1
3
2
00
00 01 11 10
1
1
2
0
3
01
01 10 00 11
3
3
0
2
1
11
11 00 10 01
2
2
3
1
0
10
10 11 01 00
3. Finalmente se obtienen un mapa para Z1 y otro para Z2 en función de X1 , X2 ,Y1 ,Y2. Z1 para el primer bit, Z2 para el segundo.
X1X2
Y1Y2 00 01 11 10
00
01
11
10
1 1
1
1
1
1
1 1
Z1 = X1Y1Y 2 + Y1X 2X1 + Y1X 2 X1 + X1Y1Y 2 + X1X2 Y1Y2 + X1X2Y1Y2
X1X2
Y1Y2 00 01 11 10
1 1
00
01
11
10
1
1
1
1
1 1
Z2 = X2 Y 2 + X 2 Y 2
1
PROBLEMA 3: Sea N un número binario de 4 bits A,B,C,D, (con A el bit más signicativo) que representa los
números decimales del 0 al 15.
Diseñar un circuito lógico cuya salida Z sea 1 si las entradas A,B,C,D representan un número que sea 0 o una
potencia de 2.
La combinación de valores correspondientes a los equivalentes binarios de los números decimales del 10 al 15
(ambos inclusive) nunca aparecerán en las líneas de entrada.
No es necesario realizar una tabla de verdad. Los numeros de las casilla corresponden al valor decimal del numero binario ABCD
AB
CD
00
01
00
1
1
11
10
1
0
01
1
4
1
5
3
7
2
6
11
10
X
1
12
8
13
9
15
11
X
X
14
X
X
10
X
F = C D+ B D +A B C
1
PROBLEMA 4: Un circuito recibe dos números binarios de tres bits A = A2,A1,A0 y B = B2,B1,B0. Diseñe un
circuito mínimo suma de productos para producir una salida siempre que A sea mayor que B.
Sin elaborar la tabla de verdad (serían 64 combinaciones) Utilizamos directamente el mapa de Karnaugh. La disposición de las
variables será tal para comparar A y B. En la casilla correspondiente colocaremos 1 o 0 dependiendo de si A es o no mayor que B.
A2 =0
A1A00 1 3 2
B1B0 00 01 11 10
B2 =0
B2 =1
A2 =1
4
5
7
6 A1A0
00
01
11
10
B1B0
0
00
1 1
1
1
1
1
1
00
1
01
1
1
1
1
1
1
01
3
11
1
1
1
1
11
2
10
1
1
1
1
10
4
00
1
1
1
00
5
01
1
1
01
7
11
6
10
1
11
1
B1B0
00 01 11 10
A1A0
00
01
10
11
10
A1A0
B1B0
F = A 2 B2 + A2 A1 B1 + B 2 A1 B1 + A2 A 0 B 1B0 + B2 A0 B1 B0 + A2A1A0 B0 + B2A1A0 B0
PROBLEMA 5: Un numero primo es aquel que es divisible sólo por sí mismo y 1. Suponga que los números
entre 0 y 31 están representados en binario en la forma de cinco bits X4,X3,X2,X1,X0, en donde x4 es el bit
más significativo. Diseñe un circuito lógico cuya salida Z será 1 cuando los cinco bits de entrada representen un
número primo.
X4=0
X4=1
X3X2
X1X0
00
00
01
1
11
1
10
1
0
1
3
2
01
1
1
4
5
11
12
1
10
13
7
15
6
14
8
9
1
11
10
00
16
1
1
01
20
17
19
18
21
1
23
22
11
28
1
1
X3X2
X1X0
10
24
29
25
31
27
30
26
00
01
11
10
F = X 4 X 3X 0 + X 4 X 3 X 2 X1 + X 4 X 2X1X 0 + X 3 X 2X 0 + X 3 X 2X1X 0 + X 4 X 2X1X 0
1
PROBLEMA 6: Un circuito recibe dos números binarios de 2 bits, Y= Y1Y0 y X=X1X0. La salida de 2 bits
Z=Z1Z0 debe ser igual a 11, si Y=X, 10 si Y>X y 01 si Y<X. Diseñe una realización mínima de suma de
productos.
Y1Y0
X 1X 0
00
01
11
10
1
1
1
1
1
1
1
00
01
11
1
10
1
1
Z1 = X 1X 0 + Y1 Y 0 + Y1X 0 + Y0 X1 + Y1X1
Y1Y0
X 1X 0
00
01
00
1
01
1
1
11
1
1
10
1
1
11
10
1
1
1
Z0 = X 1X 0 + Y1 Y 0 + Y1X0 + Y 0X1 + Y1X1
PROBLEMA 7: Se desea diseñar un circuito que avise a una estación central cuando un semáforo esta
dañado.
FUNCIONAMIENTO NORMAL
RA
V
0
1
FUNCIONAMIENTO ANORMAL
00
01
11
10
1
1 1 1
F = R A V + AV + RV