VALORACIÓN CONTINGENTE El Análisis de Datos en el Enfoque

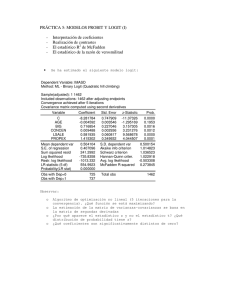
VALORACIÓN CONTINGENTE
El Análisis de Datos en el Enfoque
de la Respuesta Dicotómica
Ing. Graciela Fasciolo
Mendoza, setiembre 2002
1. INTRODUCCIÓN
La técnica de la respuestas dicotómica o de “referéndum” es uno de los enfoques más
recomendadas para encarar la valoración de un cambio ambiental, utilizando el MVC, el
que se utiliza para realizar inferencia sobre la disposición a pagar de una población de
usuarios o beneficiarios (Fasciolo G. y V.Mendoza, 2002). Se realizan encuestas, seleccionando a los entrevistados, mediante muestreo probabilístico. En el análisis inferencial se utilizan las técnicas estadísticas que proporciona el análisis de regresión.
El enfoque de respuesta dicotómica se le pregunta al encuestado si está dispuesto o no a
pagar un monto específico por el bien ambiental. Dicho monto corresponde a un valor
puntual surgido de un rango de valores. Se llama de respuesta dicotómica (ó binaria)
debido a que el encuestado tiene solo dos posibilidades de respuesta, Si ó No.
Se asignan a cada entrevistados en forma aleatoria, uno de los diferentes montos seleccionados dentro del rango de valores. Estos son diseñados de manera que abarcan una
gran gama de posibles valores para la máxima disposición a pagar.
La gama "o rango" de valores se elige con trabajo de campo en "grupos focales" con un
pequeño número de participantes, heterogéneos en cuanto a sus opiniones y condiciones
socioeconómicas. Se diseñan cuestionarios "preliminares" y se hace una discusión abierta
para fijar el límite superior e inferior del rango. Este se divide en 6 a 8 valores siendo
cada uno de ellos asignado en forma aleatoria a cada entrevistado.
Para inferir el valor promedio de la máxima disposición a pagar, o el mínimo resarcimiento exigido, por el cambio ambiental de la acción o proyecto que se evalúa, se utiliza
la función logit dentro del marco del análisis de la regresión. La respuesta es la variable
binaria, No, Si, que se cuantifica como 0, 1 respectivamente y el precio por el que responde cada entrevistado es la variable independiente o estímulo. El modelo pronostica la
probabilidad de rechazar la oferta para diferentes precios. El valor de máxima disposición a pagar que corresponde al 50% de la probabilidad (Pi=0,50) , implica el 50% de la
población y corresponde a la estimación del valor medio de disposición a pagar de la
población bajo estudio. Este monto multiplicado por el número de beneficiarios se utiliza
como el monto del beneficio (o del costo) del proyecto.
En el siguiente punto se desarrolla un breve repaso de los conceptos incluidos en la teoría
de la regresión y se deriva la función logit. En el item 3 se presenta un breve resumen de
los pasos que se deben seguir para realizar una modelación estadística para la aplicación
segura de la misma en la inferencia de valores poblacionales a partir de datos muestrales.
En el itme 4 se presenta el modelo lineal general debido a que éste es el enfoque actual
para tratar el modelo logit y el que utilizan los software estadísticos, los que son necesarios para obtener, tanto las estimaciones de los parámetros del modelo como las pruebas
de inferencia. Finalmente se presenta un ejemplo sencillo de ajustamiento de un modelo
logit con software estadístico.
3
VALORACIÓN CONTINGENTE
El Análisis de Datos en el Enfoque
de la Respuesta Dicotómica
Ing. Graciela Fasciolo
Setiembre 2002
INDICE
1. INTRODUCCIÓN................................................................................................................................3
2. EL MODELO DE REGRESIÓN SIMPLE LINEAL ..................................................................................4
3. LA MODELACIÓN ESTADÍSTICA.......................................................................................................6
3.1. La postulación de un modelo teórico......................................................................................6
3.2. La estimación de los parámetros del modelo teórico.............................................................7
3.3. La verificación del modelo mediante inferencia estadística ..................................................8
4. EL MODELO LINEAL GENERAL (MLG) .............................................................................................8
4.1. Componentes ...........................................................................................................................9
El componente aleatorio o variable respuesta, Y. ..................................................................9
El componente sistemático ......................................................................................................9
El link o enlace ..........................................................................................................................9
4.2. Linealización del modelo logit .............................................................................................. 10
5. ALGUNAS PRUEBAS PARA LA VALIDACIÓN DEL MODELO........................................................ 10
6. EJEMPLIFICACIÓN DE LA ESTIMACIÓN E INTERPRETACIÓN DE UN MODELO LOGIT .............. 11
7. BIBLIOGRAFÍA................................................................................................................................ 16
2
2. EL MODELO DE REGRESIÓN SIMPLE LINEAL
El análisis de la regresión simple lineal (RSL) está dirigido a estimar o predecir el valor
medio o promedio poblacional de una variable dependiente (Y) con base a valores fijos de
la variable independiente (X). Es así que el concepto de RSL de la población es el siguiente:
µ y = E (Y / Xi) = f ( Xi)
(1)
En donde E (Y / Xi) representa el trazado sobre las medias condicionales de Y dado Xi.
(esperanza o valor promedio de la variable dependiente para valores fijos de la variable
independiente). Es decir que la media µ y es función de X. Si f es una función lineal se
puede esquematizar en la siguiente expresión:
E (YX i ) = β o + β 1 X i
Ó simplemente µ = β 0 + β 1 x
(2)
El término de la derecha se conoce como el predictor lineal.
En el caso de que Y sea variable dicotómica (con valores 0,1), la esperanza de Y dado Xi,
puede interpretarse como la probabilidad condicional de que el evento ocurra (Y=1) dado
Xi, o sea, E(YXi) = P(Yi=1Xi).
Si Pi es la probabilidad de que Y=1, entonces (1-Pi) es la probabilidad de que Y=0 lo que
corresponde a una distribución de probabilidades de tipo binomial:
Yi
0
1
Probabilidad
(1-Pi)
Pi
Entonces, E(Y Xi) = [ 0 x (1-Pi) ] + [ 1 x Pi ] = Pi
Y entonces,
Pi = β o + β 1 X i
(3)
De este modo la esperanza condicionada de Y dado Xi puede interpretarse como la probabilidad condicionada de que Y=1 dado Xi. O sea que da la probabiidad de que el evento
ocurra para cada valor de la variable dependiente.
Por ejemplo, Si Y representa la variable Tiene Auto y X el Nivel de Ingreso, la
E(Y =1Xi) representa la probabilidad de que una familia Tenga Auto, dado un Nivel de
Ingreso, Xi. La encuesta para la recolección de datos originaría la variable dicotómica Yi
(tiene, 1; no tiene, 0) y la variable cuantitativa, ingreso familiar del encuestado, X i.
4
Para que esto sea veraz, es necesario que:
0 < E (Y = 1X i ) < 1 , para satisfacer el 1ro y 2do axioma de probabilidad, o sea que Y esté
entre 0 y 1 para que represente un valor de probabilidad.
Ahora, si para varios niveles de ingreso y varias respuestas de Y (0,1), se desea ajustar un
modelo lineal, como en (3) la probabilidad, resultará para algunos ingresos con valores
negativos y para otros valores superiores a 1. Podría pensarse en un modelo truncado en 1;
Sin embargo, tampoco satisface el hecho de que la tasa marginal de la probabilidad para
cambios en el ingreso, β 1 sea constante, como ocurre en el modelo lineal. Se necesita un
modelo que, al igual que el lineal, la E( Y = 1X i ) , o sea la probabilidad de tener auto, aumente cuando el ingreso Xi aumenta.
Pero se necesita además que la relación entre la probabilidad de tener un auto y el ingreso
no sea lineal; es decir que la tasa de crecimiento de la probabilidad no sea constante. Esto
significa que la probabilidad se acerca a 0 a tasas cada vez menores, cuando el ingreso Xi
es muy pequeño, y se acerca a 1 a tasas muy pequeñas, cuando Xi es muy grande.
En definitiva, se trata de un modelo de tasa de crecimiento no constante, con un techo en
1. Este esquema puede proporcionarlo la función logística. En el caso de que Y sea variable dicotómica (0,1) el modelo se reconoce como logit y está representado en la Fig. 1a ,
su función es la siguiente :
Pi = E (Y = 1 / X i ) =
1
1+ e
−( β 0 + β1 X i )
(4)
En el ejemplo visto representa la probabilidad de tener auto, dado un nivel de ingreso, Xi.
Puede interpretarse como una función de distribución acumulativa, que proviene de una
función de densidad simétrica y en donde la mediana es igual a la media. La mediana Xmd
puede despejarse de la ecuación cuando el valor de probabilidad es 0,5:
0,5 =
1
1+ e
− ( β 0 + β1 Xmd )
despejando Xmd se obtiene:
X md = −
β0
β1
(5)
La mediana es a su vez la media, en el modelo logit. Por lo tanto habrá que obtener las
estimaciones de β0 y β1 para derivar la mediana del ingreso de las personas.
En el enfoque de la respuesta dicotómica del MVC, se le pregunta al encuestado si está
dispuesto a pagar un determinado monto por el bien ambiental y su respuesta será si o no;
los valores que se fijan para Xi se originan a partir de un rango de diseño que surge del
focus grup. En este caso cuando aumenta el precio o impuesto, Xi, disminuye, teóricamente, la probabilidad de aceptación del monto ofertado, o sea que la curva logit tendrá
pendiente negativa, como en la Fig 1b.
5
G(x)
Probabilidad
1
1 - G(x)
Probabilidad
1
0,5
0,5
0
x (precio)
Figura 1a
0
x (precio)
Figura 1b
En la práctica, la encuesta brinda la base de datos correspondientes a cada valor ofertado y
a su respuesta, a partir de los cuales deben obtenerse las estimaciones de β0 y β1 para
derivar la media de la máxima disposición a pagar por el bien ambiental.
3. LA MODELACIÓN ESTADÍSTICA
Los pasos para obtener una ecuación predictiva para aplicar a un fenómeno económico o
social, que responde a un modelo teórico, son los siguientes:
3.1. La postulación de un modelo teórico
El modelo estadístico combina una parte sistemática con una parte aleatoria. Así para cada
valor de la variable Yi será:
Yi = f ( x ) + ε i
(6)
O sea que la variable aleatoria Y se descompuso en una parte sistemática, que es la función
o ecuación matemática y en una parte aleatoria. Entre los supuestos importante para el modelo de RSL se destaca el que hace referencia a la distribución de probabilidades de Y por
lo tanto del error ε i . Para éste se acepta que tiene la misma distribución que Y, y que ésta
es normal con media 0 y varianzas constante.
Por lo tanto al enunciar el modelo, es importante especificar la distribución de probabilidades de la variable respuesta Y. Las distribuciones que más se utilizan en los modelos estadísticos son:
6
a) Distribución binomial. Las observaciones son binarias o dicotómicas en cada unidad
de análisis1 (éxito o fracaso, sí o no, defectuoso o no defectuoso, etc).
b) Distribución de Poisson. Las observaciones provienen de recuentos o “conteos”, en
cada unidad de análisis (0,1, 2, 3, ...).
c) Distribución normal. Las observaciones provienen de variables cuantitativas.
Como se dijo, el modelo logit está basado en la distribución binomial.
En el método de respuesta dicotómica, se postula que la probabilidad de pagar un monto
determinado por un bien ambiental disminuye a medida que el monto aumenta, pero no a
una tasa constante sino a tasa variable, según un modelo logit, cuya función f(x) es (4) y
β 1 es negativa.
3.2. La estimación de los parámetros del modelo teórico
La función o parte sistemática del modelo contiene constantes β 0 , β 1 ,... , que son los parámetros del modelo y que hasta el momento son desconocidos. El paso siguiente es estimarlos. Los valores que se obtienen se conocen como las estimaciones y las funciones que
se utilizan para obtenerlos como estimadores.
Se utilizan principalmente dos métodos de estimación: a) el Método de Mínimos Cuadrados (MC) y el Método de Máxima Verosimilitud (MV). Para algunos modelos este último
es mejor pero en muchos casos se obtiene con ambos el mismo resultado. Los dos procedimientos derivan fórmulas o funciones (estimadores de los β j ) que permitirán obtener las
estimaciones.
El método de MC obtiene los estimadores de β 0 y β 1 minimizando la suma de cuadrados
entre los valores observados y los valores estimados.
El método de MV parte de la función de verosimilitud. Esta es la función de densidad de
probabilidad conjunta que da la probabilidad de un conjunto de datos observados, expresada en función de los parámetros, función de máxima verosimilitud. Los estimadores de
MV son aquellos que permiten obtener los valores de los parámetros (estimaciones) que
maximizan la probabilidad (de que se presenten esos valores) para los datos observados.
Para obtenerlos se maximiza el logaritmo de la función de verosimilitud mediante las derivadas parciales con respecto a los parámetros.
1
La unidad de análisis es la unidad estadística o de medición.
7
3.3. La verificación del modelo mediante inferencia estadística
Habiendo obtenido las estimaciones de los parámetros, es decir una vez que se ha cuantificado la parte sistemática de la ecuación dándole valores a β 0 y β 1 , la tarea siguiente consiste en desarrollar los criterios apropiados para determinar si las estimaciones obtenidas
están de acuerdo con lo que se espera de la teoría. La refutación o confirmación se fundamenta en la rama de la teoría estadística conocida como inferencia estadística.
Se puede particionar la variabilidad total observada en los datos en la porción atribuible a
la parte sistemática (mediante un proceso algebraico que involucre a todas las observaciones) y el resto se atribuye a la parte aleatoria, según (6). Un buen modelo será aquel que
explique gran parte de la variabilidad de Y. O sea que la variabilidad de la parte sistemática sea muy grande con relación a la de la parte aleatoria.
Esto debe balancearse con el hecho deseado de tener un modelo “simple”. A veces se consiguen modelos muy complejos que explican gran parte de la variabilidad pero en la práctica no son fáciles de manejar. Una regla en estadística aplicada es preferir modelos simples, que describan adecuadamente los fenómenos.
El proceso para obtener criterios que permitan tomar decisiones con respecto a la utilidad
del modelo requiere de la inferencia estadística.
Se pueden clasificar las pruebas para la verificación de los modelos en dos grandes grupos:
a) Pruebas de bondad de ajuste para el modelo global; la hipótesis estadística comprende
a todos los parámetros.
b) Pruebas de hipótesis para cada uno de los parámetros.
Para cada método de estimación se han desarrollado una serie de pruebas de hipótesis (o de
significancia como se las conoce comúnmente) y cada paquete estadístico presenta alguna
de ellas, generalmente con referencias bibliográficas para poder interpretarlas.
4. EL MODELO LINEAL GENERAL (MLG)
El modelo de RSL postula que la variable dependiente Y tiene distribución Normal Se
vió que en el modelo logit, ésta es binomial. Los recientes avances en la teoría estadística
y en los software de computación han permitido usar métodos análogos a aquellos desarrollados para el modelo de RLS en las siguientes situaciones:
a) Cuando las variables respuestas tienen distribuciones diferentes que las de la distribución normal y resultan ser categóricas en lugar de continuas. Este avance se ha producido al reconocer que muchas de las importantes propiedades de la distribución normal
se dan también en una amplia clase denominada la familia exponencial. Esta familia
comprende, además de la distribución normal la distribución binomial y la distribución
de Poisson.
8
b) Cuando la variable respuesta no es necesariamente, función lineal (en los parámetros),
pero puede obtenerse una función de aquella que sí es lineal. Esto permite estimar parámetros de funciones de una combinación lineal.
Por otro lado, estas estimaciones que comprenden una gran cantidad de cálculos hoy en día
son posibles con los sofisticados software estadísticos para PC.
Dentro de este contexto, la unicidad de muchas técnicas estadísticas que comprenden combinaciones lineales de los parámetros la da este modelo lineal general (MLG). Comprende
una amplia clase de modelos que van desde la regresión lineal ordinaria, ponderada y el
análisis de la varianza (ANOVA) para variables continuas (datos cuantitativos), hasta
modelos para otras variables de tipo discreta (datos categóricos).
4.1. Componentes
El modelo lineal general (MLG) tiene 3 componentes básicos:
El componente aleatorio o variable respuesta, Y.
Su distribución de probabilidades debe pertenecer a la familia exponencial: distribución
Normal, Binomial o Poisson, originando cada una de ellas el tipo de datos que se mencionó
previamente.
El componente sistemático
Es una combinación lineal de las variables explicativas del tipo: β0 + β1X + ... y se lo conoce como el predictor lineal (en los parámetros).
El link o enlace
Une el componente aleatorio con el componente sistemático. Especifica a que es igual la
media µ para cada valor observado. En RL se dijo que la media µ es igual a la E(Y ). El
MLG permite que el componente sistemático se relaciones con la media µ a través de una
función g (µ), de la misma y el link es la función especificada para la media. De esta manera.
g ( µ ) = β 0 + β 1 X i + ... , siendo g (µ ) la función link o enlace
La más simple de las funciones link es cuando g (µ ) es la media misma o sea:
g ( µ ) = µ = E (Y ) y se llama link identidad ó identity link
Otros link permiten que la media se relacione en forma no lineal con el predictor.
Cuando g ( µ ) = log( µ ) = log E (Y ) . En este caso µ no puede ser negativo.
Este modelo se llama loglineal y se utiliza en datos de recuentos provenientes de distribución Poisson.
9
µ
(7) modela el logaritmo natural de los odds que es la
(1 − µ )
relación entre la probabilidad favorable y la desfavorable . En este caso µ =P, probabilidad. Se conoce como el logit link porque permite modelar la función logística (4) cuando
la variable respuesta es binomial con respuestas 0,1 y se pronostican valores de probabilidad, P(Y=1/X) 2.
La función link g ( µ ) = log
4.2. Linealización del modelo logit
El modelo logit es parte del MLG. El componente aleatorio responde a una variable respuesta binomial, y la función link toma la forma expresada en (7), en donde log es logaritmo natural.
Expresa la relación entre la probabilidad favorable y la desfavorable . En este caso µ =P,
P
la probabilidad de respuesta positiva. Su ecuación de predicción, log( i ) = β 0 + β 1 xi
1 − Pi
(8), permite pronosticar valores de probabilidad. Esta función link surge de una transformación logarítmica de la función logit. Mediante un poco de álgebra en ( 4 ) se llega a la
ecuación (8). Esta ecuación representa una función lineal en los parámetros. Actualmente
son muchos los software estadísticos que permiten ajustar esta función logit .En el MVC la
base de información aportada por la encuesta provee las respuestas de las personas en
valores 0, 1 y los precios ofertados en cada una de ellas. La salida de este análisis brindará
los valores estimados para β0 y para β1. El cociente entre ambos, según (6), es la estimación promedio de la máxima disposición a pagar.
5. ALGUNAS PRUEBAS PARA LA VALIDACIÓN DEL MODELO
Con respecto a las pruebas de inferencia estadística para verificar el modelo, el método de
MC, bajo el supuesto de distribución normal para Y, utiliza el Análisis de la Varianza
(ADEVA) para bondad de ajuste; la razón entre la varianza explicada por el modelo y la
varianza del término aleatorio que tiene una distribución F (conocida como la Prueba de
F) es el estadígrafo que se utiliza. También se presenta generalmente el coeficiente de determinación, R2 , que es una medida matemática de la bondad de ajuste que da información
sobre que porción de la variabilidad total de la variable respuesta Y, está explicada por la
variable independiente3.
Los estadísticos z o t son utilizados para las pruebas de hipótesis para cada uno de los parámetros.
2
La función logística que no es lineal en los parámetros puede ser intrínsicamente lineal cuando el techo
es 1 o sea la máxima probabilidad acumulada. Pero es lineal no para la probabilidad de ocurrencia sino
para el log de la relación entre la probabilidad favorable y la desfavorable (odds = p/(1-p)).
3
Se debe ser cuidadoso en su interpretación porque si el cálculo de R2 no está acompañada por su prueba
de significancia pude llevar a conclusiones irrelevantes. Por otro lado en los modelos linealizados mediante transformaciones, la interpretación de R2 es diferente.
10
El MLG, cuando utiliza el método de MV, evalúa la bondad de ajuste del modelo mediante la prueba de la razón de máxima verosimilitud que tiene una distribución Jicuadrado. Para pruebas de hipótesis para los parámetros también pruebas de z o el estadístico Wald (que es z2) y tiene distribución Ji-cuadrado.
Los software estadísticos (ó econométricos) contiene diferentes pruebas de bondad de ajuste. Generalmente se acompañan en los manuales de los mismos ó en las funciones de ayuda ejemplos, que mostrarán como interpretar las salidas.
También es importante destacar que la mayoría de los software presentan dos alternativa
para ingresar la base de datos. Una de ellas es utilizando la información primaria, tal como
fue recolectada, es decir el valor del precio ofertado y la respuesta cuantificada como 0 ó 1.
La otra es con los datos de la encuesta semiprocesados, es decir, para cada precio la cantidad de respuestas positivas y la cantidad de negativas.
6. EJEMPLIFICACIÓN DE LA ESTIMACIÓN E INTERPRETACIÓN DE UN
MODELO LOGIT
A continuación se presenta la salida de dos software estadísticos (Stata y Statgraph) para el
análisis logit. El ejemplo completo se verá por separado y pertenece a la tesina de la licenciatura en Economía del Alejandro Gallego, dirigida por el Dr. Armando Llop (Gallego, A,
1999).
El objetivo del estudio es la evaluación económica del proyecto de parquizar un terreno de
19 has ubicado en la estación del Ferrocarril General San Martín en la ciudad de Mendoza.
La pregunta de valoración fue :¿Si se realiza el proyecto, estaría dispuesto a pagar una
tasa Ecológica bimestral , para su construcción y mantenimiento durante 10 años de.....?
El vehículo de pago es la tasa municipal y los valores ofertados son $ : 1, 3, 5, 7 y 9.
La variable respuesta es PAGA (0,1), siendo PRECIO la variable estímulo (1, 3, 5 y, 7 y 9).
Se realizaron 80 encuestas; la base de datos presenta (parcialmente, pues hubo más preguntas) esta forma:
11
noenc direcc tasa precio paga
1
6
14
1
1
2
1
15
1
1
3
5
13
1
1
4
3
21
1
1
9
2
24
1
1
10
3
13
1
1
11
4
20
1
1
12
6
19
1
1
13
4
13
1
1
14
6
37
1
1
15
6
15
1
1
16
3
13
1
1
18
1
38
1
1
19
6
23
1
0
20
2
20
1
1
22
4
13
3
1
23
2
15
3
0
24
2
13
3
1
27
6
25
3
0
28
4
38
3
1
31
4
19
3
1
32
4
13
3
1
37
6
20
3
0
38
2
16
3
1
39
4
29
3
1
42
4
13
5
0
43
6
15
5
0
46
2
15
5
1
47
2 121 5
0
48
5
30
5
0
49
4
37
5
0
50
6
20
5
1
52
6
13
5
0
54
1
14
5
1
55
6
18
5
1
56
2
13
5
0
58
3
13
5
1
59
5
18
5
1
61
2
19
7
0
62
5
18
7
1
63
3
13
7
1
noenc direcc tasa precio paga
65
5
26
7
0
66
4
19
7
1
68
1
14
7
1
73
3
63
7
0
75
6
13
7
0
77
6
13
7
1
78
2
27
7
1
79
6
21
7
1
81
3
13
9
0
82
2
36
9
1
84
5
40
9
0
83
3
13
9
1
86
5
22
9
0
88
2
28
9
1
89
5
49
9
1
92
6
58
9
0
93
1
13
9
1
94
2
19
9
0
95
3
14
9
1
98
4
19
9
1
100
2 105 9
0
101
4
13
1
1
103
6
44
1
0
110
5
18
1
1
113
2
13
3
1
114
6
13
3
0
116
2
46
3
0
118
6
13
3
1
119
3
24
3
1
122
3
15
5
1
124
4
41
5
1
130
4
27
5
1
131
6
14
7
1
132
6
32
7
0
138
5
30
7
1
139
1
69
7
0
141
6
66
9
0
144
2
13
9
0
146
5
46
9
0
148
3
13
9
0
149
2
14
9
1
12
1) Salida del Programa Stata
logit paga precio
Iteration 0: log likelihood = -53.850383
Iteration 1: log likelihood = -50.200716
Iteration 2: log likelihood = -50.168213
Iteration 3: log likelihood = -50.168197
Logit estimates
Number of obs =
Log likelihood = -50.168197
paga
Coef.
Std. Err.
precio -.2230369 .0858368
cons
1.721133 .5292022
82
LR chi2(1)
=
7.36
Prob > chi2
=
0.0067
Pseudo R2
z
P>|z|
=
0.0684
[95% Conf. Interval]
-2.598 0.009
-.3912739
-.0548
3.252 0.001
.6839155
2.75835
El estadígrafo para la bondad de ajuste del modelo es Ji cuadrados cuya probabilidad es
0,007, valor suficientemente pequeño para considerar que el modelo se ajusta.
En el cuadro precedente se presentan las estimaciones para los coeficiente de regresión
siendo, βˆ1 = −0,223 (precio) y βˆ 0 = 1,721 (cons). Las pruebas de hipótesis para los dos
coeficientes muestran valores significativos, ya que sus valores de probabilidad son pequeños (0,009 y 0,001 respectivamente).
P
El modelo ajustado es: log( i ) = 1,721 − 0,223PRECIO .
1 − Pi
Por lo tanto se puede utilizar para inferir el valor promedio o mediana utilizando la ecuación (6):
X md = −
1,721
= 7,718
− 0,223
Este valor promedio de $7,7 multiplicado por el tamaño de la población de inferencia o
sea de la población beneficiaria da el beneficio del proyecto.
El programa da la posibilidad de realizar el gráfico como también de estimar las probabilidades de máxima disposición a pagar (Pi), para cada precio.
2) Salida del Programa Statgraph
En este programa se ha utilizado la columna 1 para la variable PRECIO y no se le ha designando nombre por lo tanto el programa la denomina Col_1. Los resultados y los indicadores son los mismos que en el Stata. Este programa trae al final una interpretación en
Stata Advisor.
13
Logistic Regression
Dependent variable: Col_2
Factors:
Col_1
Estimated Regression Model (Maximum Likelihood)
-----------------------------------------------------------Standard
Estimated
Parameter
Estimate
Error
Odds Ratio
-----------------------------------------------------------CONSTANT
1,72113
0,528977
Col_1
-0,223037
0,0858113
0,800085
-----------------------------------------------------------Analysis of Deviance
--------------------------------------------------Source
Deviance
Df
P-Value
--------------------------------------------------Model
7,36437
1
0,0067
Residual
100,336
80
0,0617
--------------------------------------------------Total (corr.)
107,701
81
Percentage of deviance explained by model = 6,83781
Adjusted percentage = 3,12382
Likelihood Ratio Tests
--------------------------------------------------------Factor
Chi-Square
Df
P-Value
--------------------------------------------------------Col_1
7,36437
1
0,0067
--------------------------------------------------------Residual Analysis
--------------------------------Estimation
Validation
n
82
MSE
0,048232
MAE
0,440828
MAPE
ME
-0,00220813
MPE
The StatAdvisor
--------------The output shows the results of fitting a logistic regression model
to describe the relationship between Col_2 and 1 independent
variable(s). The equation of the fitted model is
Col_2 = exp(eta)/(1+exp(eta))
where
eta = 1,72113 - 0,223037*Col_1
Because the P-value for the model in the Analysis of Deviance table is
less than 0.01, there is a statistically significant relationship
between the variables at the 99% confidence level. In addition, the
P-value for the residuals is less than 0.10, indicating that the model
is significantly worse than the best possible model for this data at
the 90% confidence level.
The pane also shows that the percentage of deviance in Col_2
explained by the model equals 6,83781%. This statistic is similar to
the usual R-Squared statistic. The adjusted percentage, which is more
suitable for comparing models with different numbers of independent
variables, is 3,12382%.
In determining whether the model can be simplified, notice that the
highest P-value for the likelihood ratio tests is 0,0067, belonging to
Col_1. Because the P-value is less than 0.01, that term is
statistically significant at the 99% confidence level. Consequently,
you probably don't want to remove any variables from the model.
14
2. ¿Porque la función Probabilidad vs Precio es la curva de demanda estimada?
En la función logit graficada en la Figura 1b, en las ordenadas están indicadas las probabilidades Pi y en abscisas los valores de máxima disposición a pagar. Si la probabilidad
se multiplica por el tamaño de la población de inferencia (N) se obtiene para cada valor
de precio la cantidad de gente que está dispuesto a pagar ese monto.
En la función de demanda agregada estudiada, se ha graficado en ordenadas el precio y la
cantidad en abscisas. Si se intercambian los ejes de ordenadas y abscisas, como se lo ha
hecho en la Figura 2, se obtiene bajo la curva, el beneficio del proyecto. Para obtener su
valor se utiliza el Precio promedio, que es el que está dispuesto a pagar el 50% de la población y se lo multiplica por N, siendo dicha área equivalente al área bajo la curva.
FIGURA 2. Curva de demanda estimada con MVC. Respuesta Dicotómica
7. BIBLIOGRAFÍA
Agresti, A., 1996. An Introduction to Categorical Data Análisis. John Wiley and Sons,
INC. New York, etc. 294 p.
Dobson, A. 1990. An introduction to generalized linear models. Chapman and Hall. London, etc. 171p.
Fasciolo G. y V. Mendoza, 2002. El método de la valoración contingente. Apuntes inéditos. INA. CELA. 6p.
Gallego, A., 1999. Valoración contingente de un espacio verde. Trabajo de investigación.
Facultad de Ciencias Económicas. UNCuyo . 83 p.
Gujarati, D.N., 1995. Econometría. Cap. 13. 2da edición. Mc. Graw –Hill Interamericana
de México S.A. 597 p.
Software estadísticos: 1) Stata 6 for windows 2) Statgrphics Plus 4.
15