Razones Trigonométricas de Ángulos Agudos I

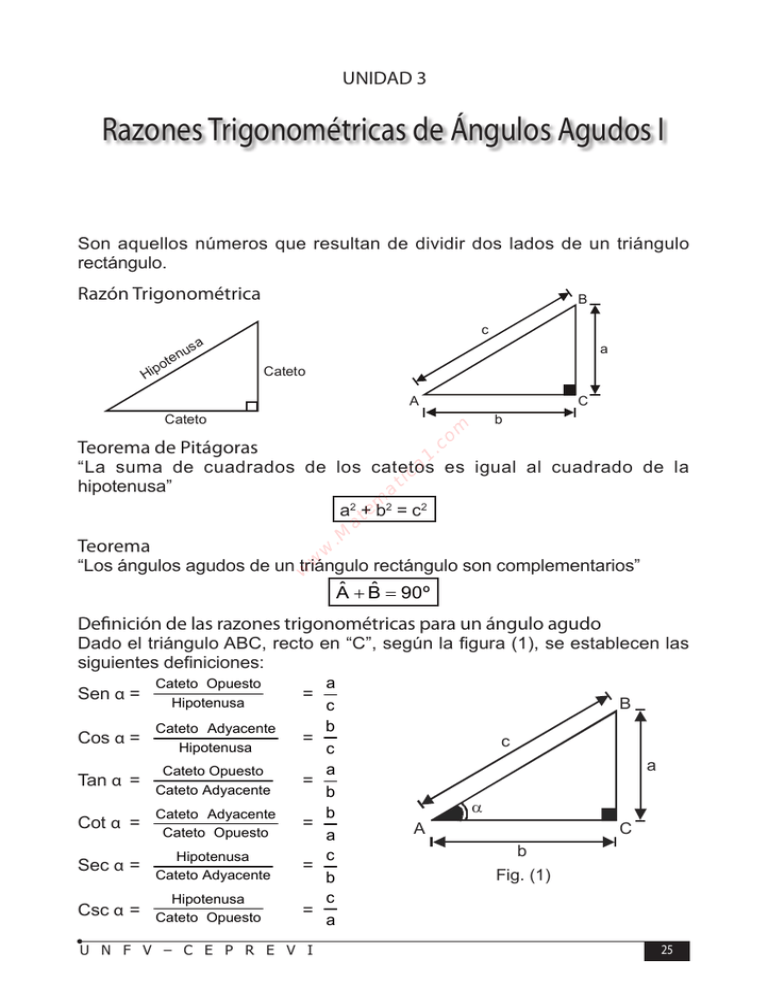
TRIGONOMETRÍA
UNIDAD 3
Razones Trigonométricas de Ángulos Agudos I
Son aquellos números que resultan de dividir dos lados de un triángulo
rectángulo.
Razón Trigonométrica
a
us
ten
o
p
Hi
B
c
a
Cateto
A
C
b
m
Cateto
o
1
.c
Teorema de Pitágoras
.M
a
te
m
a
ti
ca
“La suma de cuadrados de los catetos es igual al cuadrado de la
hipotenusa”
a2 + b2 = c2
w
Teorema
w
w
“Los ángulos agudos de un triángulo rectángulo son complementarios”
ˆ + Bˆ =
A
90º
Definición de las razones trigonométricas para un ángulo agudo
Dado el triángulo ABC, recto en “C”, según la figura (1), se establecen las
siguientes definiciones:
Sen α=
Cos α=
Tan α=
Cot α=
Sec α=
Csc α=
a
c
b
Cateto Adyacente
=
Hipotenusa
c
a
Cateto Opuesto
=
Cateto Adyacente
b
b
Cateto Adyacente
=
Cateto Opuesto
a
c
Hipotenusa
=
Cateto Adyacente
b
c
Hipotenusa
=
Cateto Opuesto
a
Cateto Opuesto
Hipotenusa
=
U N F V – C E P R E V I
B
c
a
α
A
C
b
Fig. (1)
25
TRIGONOMETRÍA
Ejemplo
En un triángulo rectángulo ABC (Ĉ = 90°), se sabe que la suma de catetos es
igual “k” veces la hipotenusa. Calcular la suma de los senos de los ángulos
agudos del triángulo.
Resolución
Nótese que en el enunciado del problema tenemos:
B
c
a
Senα + Senβ =
α
A
a+b=k·c
Nos piden calcular:
β
b
Luego: Senα + Senβ =
C
a b a+b
+ =
c
c c
k•c
=K
c
ca
1
.c
o
m
Ejemplo
Los tres lados de un triángulo rectángulo se hallan en progresión arítmetica,
hallar la tangente del mayor ángulo agudo de dicho triángulo.
Teorema de Pitágoras
(x - r)2 + x2
x2 + 2xr + r2 + x2
x2 - 2xr x2
w
w
x+r
w
Cateto menor = x - r
Cateto mayor = x
Hipotenusa = x + r
.M
a
te
m
a
ti
Resolución
Nótese que dado el enunciado, los lados del triángulo están en progresión
aritmetica, de razón “r” asumamos entonces:
= (x + r)2
= x2 +2xr + r2
= 2xr
= 4xr →
x
x-r
Fig. (A)
x = 4r
Importante
“A mayor cateto, se opone mayor ángulo agudo”; luego, reemplazando en la
figura (A), tenemos:
Nos piden calcular: Tanα =
4r 4
=
3r 3
5r
4r
α
3r
26
U N F V – C E P R E V I
TRIGONOMETRÍA
Ejemplo
Calcular el cateto menor de un triángulo rectángulo de 330 m de perímetro, si
la tangente de uno de sus ángulos agudos es 2,4.
Resolución
1º Sea “α” un ángulo agudo del triángulo que cumpla con la condición:
Tan α = 2,4 =
24 12
=
10 5
Ubicamos “α” en un triángulo rectángulo, cuya relación de catetos guardan la
relación de 12 a 5.
La hipotenusa se calcula por pitágoras
Triángulo Rectángulo Particular
13
Triángulo Rectángulo General
13K
12
12K
α
m
α
5K
ca
1
.c
o
5
w
w
w
.M
a
te
m
a
ti
2º El perímetro del triángulo rectángulo es:
Según la figura:
5K + 12K + 13K= 30 K
Según dato del enunciado:
= 330 m
Luego:
30K= 330
K= 11
3º La pregunta es calcular la longitud del menor cateto es decir:
Cateto
= 5K
= 5 · 11 m
= 55 m
Propiedades de las Razones Trigonométricas
Razones Trigonométricas Recíprocas
“Al comparar las seis razones trigonométricas de un mismo ángulo agudo,
notamos que tres pares de ellas al multiplicarse nos producen la unidad”.
La parejas de las R.T. recíprocas son entonces:
Seno y Cosecante:
Senα • Cscα = 1 
Coseno y Secante:
Cosα • Secα = 1  Nótese: “ángulos
Tangente y Cotangente:
Tanα • Cotα = 1  iguales”
U N F V – C E P R E V I
27
TRIGONOMETRÍA
Ejemplo
Indicar la verdad de las siguientes proposiciones:
I. Sen20º • Csc10º = 1
II. Tan35º • Cot50º = 1
III.Cos40º • Sec40º = 1
Resolución
Nótese que en las parejas de razones trigonométricas recíprocas el producto
es “1”; siempre que sean ángulos iguales.
Luego: Sen20º • Csc10º ≠ 1; sus ángulos NO son iguales
Tan30º • Cot50º ≠ 1; sus ángulos NO son iguales
Cos40º • Sec40º = 1; sus ángulos SI son iguales
∴ I) F
II) F
III) V
m
Ejemplo
Resolver “x”. Ángulo agudo que verifique:
Tan(3x + 10º + α) • Cot(x + 70º + α) = 1
a
.M
ANGULOS IGUALES
w
te
m
a
ti
ca
1
.c
o
Resolución
Nótese que en la ecuación intervienen, razones trigonométricas recíprocas;
luego los ángulos son iguales.
Tan(3x + 10º + α)•Cot(x + 70º + α ) = 1
w
w
3x + 10º + α = x + 70º + α
2x = 60º
x = 30º
Ejemplo
Se sabe:
Calcular:
Senθ • Cosθ • Tanθ • Cotθ • Secθ =
3
7
E = Cosθ • Tanθ • Cotθ • Secθ • Cscθ
Resolución
Recordar:
Cosθ • Secθ = 1
Tanθ • Cotθ = 1
Secθ • Cscθ = 1
Luego, reemplazando en la condición del problema:
3
Senθ •
Cosθ • Tanθ
• Cotθ • Secθ=


7
1
3
Senθ=
... (I)
7
28
U N F V – C E P R E V I
TRIGONOMETRÍA
Nos piden calcular:
E = 
Cosθ • Tanθ
• Cotθ • Secθ

• Cscθ
1
E = Cscθ =
∴ E =
7
3
1
3
, pero de (I) tenemos: Senθ =
7
Senθ
Razones trigonométricas de ángulos complementarios
“Al comparar las seis razones trigonométricas de ángulos agudos, notamos
que tres pares de ellas producen el mismo número, siempre que su ángulos
sean complementarios”.
NOTA:
“Una razón trigonométrica de un ángulo es igual a la co-razón del ángulo
complementario.”
CO-RAZÓN
Seno
Coseno
Tangente
Cotangente
Secante
Cosecante
m
a
ti
ca
1
.c
o
m
RAZÓN
a
te
Dado: α + β = 90º, entonces se verifica:
w
w
w
.M
Senα = Cosβ
Así por ejemplo:
A) Sen20º = Cos70º
Tanα = Cotβ
Secα = Cscβ
B) Tan50º = Cot40º
C)Sec80º = Csc10º
Ejemplo
Indicar el valor de verdad según las proposiciones:
I. Sen80º = Cos20º
II. Tan45º = Cot45º
III.Sec(80º – x) = Csc (10º + x)
U N F V – C E P R E V I
29
TRIGONOMETRÍA
Resolución
Nótese que dada una función y cofunción serán iguales al evaluar que sus
ángulos sean complementarios.
I. Sen80º ≠ Cos20º; Sin embargo: Sen80º = Cos10º
Suman 90°
Porque suman 100°
II. Tan45º = Cot45º
Suman 90°
III.Sec(80º – x) = Csc (10º + x)
Suman 90°
Ejemplo
Resolver el menor valor positivo de “x” que verifique:
Sen5x = Cosx
.M
a
te
m
a
ti
ca
1
.c
o
m
Resolución
Dada la ecuación sen5x = Cosx; luego los ángulos deben sumar 90º
entonces:
5x + x = 90º
6x = 90º
x = 15º
w
w
w
Ejemplo
Resolver “x” el menor positivo que verifique:
Sen3x – Cosy = 0
Tan2y • Cot30º – 1 = 0
Resolución
Nótese que el sistema planteado es equivalente a:
Sen3x = Cosy ⇒ 3x + y = 90º
(R.T. ángulos complementarios)
Tan2y • Cot30º = 1 ⇒ 2y = 30º (R.T. recíprocas)
De la segunda igualdad: y = 15º
Reemplazando en la primera igualdad:
3x + 15º = 90
3x = 75º
x = 25º
Ejemplo
Se sabe que “x” e “y” son ángulos complementarios, además:
Senx = 2t + 3
Cosy = 3t + 4,1
Hallar: Tan x
30
U N F V – C E P R E V I
TRIGONOMETRÍA
Resolución
Dado: x + y = 90º → Senx = Cosy
Reemplazando:
2t + 3= 2t + 4,1
–1,1 = t
Conocido “t”, calcularemos: Senx= 2(–1, 1) + 3
Senx= 0,8
Senx=
4
5
... (I)
Nota:
Conocida una razón trigonométrica, luego hallaremos las restantes;
graficando la condición (I) en un triángulo rectángulo, tenemos:
5
4
Tanx =
⇒
x
3
.c
o
m
Por Pitágoras
Cateto Opuesto
4
=
Cateto Adyacente 3
ca
1
Razones trigonométricas en ángulos notables
a
te
m
a
ti
I. Triángulos rectángulos notables exactos
* 30º y 60º
.M
60º
w
60º
w
w
2
1
2k
⇒
30º
30º
k√3
√3
1k
* 45º y 45º
45º
√2
45º
1
45º
⇒
k√2
k
45º
1
U N F V – C E P R E V I
k
31
TRIGONOMETRÍA
II. Triángulos rectángulos notables aproximados
* 37º y 53º
53º
53º
5
5k
⇒
3
3k
37º
37º
4k
4
* 16º y 74º
74º
25
74º
⇒
7
25k
16º
7k
16º
24
m
24k
30º
60º
45º
Sen )<
1/ 2
3 /2
2 /2
Cos )<
3 /2
1/ 2
Tan )<
3 /3
Cot )<
3
Sec )<
Csc )<
53º
m
3/ 5
4/ 5
2 /2
4/ 5
3/ 5
24 / 25 7/ 25
3
1
3/ 4
4/ 3
7/ 24
24 / 7
3 /3
1
4/ 3
3/ 4
24 / 7
7/ 24
2 3 /3
2
2
5/ 4
5/ 3
25 / 24 25 / 7
2
2 3 /3
2
5/ 3
5/ 4
25 / 7 25/ 24
w
.M
a
te
a
ti
37º
w
R.T.
ca
)<
w
1
.c
o
Tabla de las razones trigonométricas de ángulos notables
16º
74º
7/ 25 24 / 25
Ejemplo
Calcular:
F=
4 • Sen30º + 3 • Tan60º
10 • Cos37º + 2 • Sec45º
Resolución
Según la tabla mostrada notamos:
1
+ 3⋅ 3
2
F=
4
10 ⋅ + 2 ⋅ 2
5
4⋅
∴
32
F=
F=
2+3 5
=
8 + 2 10
1
2
U N F V – C E P R E V I
TRIGONOMETRÍA
Ejemplo
9θ
Sen3θ • Cos6θ • Csc  
 2 
Sea:F(θ) =
9θ
Tan3θ • Sec6θ • Cot  
 2 
Evaluar para: θ = 10º
Resolución
Reemplazando θ = 10º en “F(θ) tenemos:
Sen30º • Cos60º • Csc45º
F(10º) =
Tan30º • Sec60º • Cot45º
Reemplazando sus valores notables tenemos:
1 1
• • 2
2
2
F(10º)=
3
• 2•1
3
Racionalizando:
F(10º) =
m
a
ti
ca
1
.c
o
m
2
3 2
4
F(10º) =
=
2 3
8 3
3
te
a
.M
w
w
w
Ejemplo
A
6
8
α
B Si ABCD es un cuadrado calcular “Tanα”
P
53º
D
C
H
Resolución
A
Como “α” no está en un triángulo rectángulo:
Luego, efectuaremos trazos de modo que “α”
y 53º estén en triángulo rectángulo.
De la figura:
M
PMD: notable de 37º y 53º,
luego suponemos DP = 5k.
Como: DP = BC = 5k
U N F V – C E P R E V I
3k
D
α
5k
4k
37º
53º
B
P
5k
5k
C
33
TRIGONOMETRÍA
Luego el lado del cuadrado mide 5K
- Sumando: PH + MD = AD
PH + 3K = 5K
∴
PH = 2K
- Sumando:
PM + HB = AB
4K + HB = 5K
∴
HB = K
PH 2K
- Finalmente:Tanα = = = 2
HB K
Ejemplo
En la figura mostrada “O” es el centro del
cuadrante AOB, hallar “Cotθ”
A
P
1
θ
m
Q
B
2
ti
H
a
2
m
O
ca
1
.c
o
3
A
.M
a
te
Resolución
Construimos un triángulo rectángulo OPH;
luego aplicando el teorema de Pitágoras
w
w
w
P
4
x
x=2 3
O
En la figura inicial trazamos QE
PE = 2 3 − 3
QE = 2
PE 2 3 − 3
=
∴Cot θ =
QE
2
2
2
H
B
PH
A
P
1
θ
E
Q
2√3
3
O
34
2
H
2
B
U N F V – C E P R E V I
TRIGONOMETRÍA
6. En un triangulo rectángulo de perímetro
60 m, calcular su área, si el coseno de
uno de los ángulos agudos es 0,8.
a) 120 m² b) 130 m² c) 140 m²
d) 150 m² e) 160 m²
Problemas I
1. De la figura, calcular:
A = Cosec θ – Ctg θ
8
x+2
7. Si se cumple:
Sen28°·Sec θ = 7Cos62°–4Sen28°;
0°<θ< 90°
Calcula:
K = Sec 45° (Tg θ + 3 Sen θ)
a) 2
b) 4
c) 6
d) 8
e) 10
x
1
1
1
b) c)
2
3
4
1
1
d) e)
5
6
a)
8. De la figura “'Sec θ" es:
2. En triangulo rectángulo la tangente
de uno de los ángulos agudos
es el triple de la tangente de su
complemento; calcular el coseno del
mayor ángulo agudo.
m
o
1
ca
ti
a
d)
b
2a
e)
a
b
9. De la figura calcular:
K = Ctg2 θ + 4 Tg α
2
Tg10° ⋅ Tg80° + Tg 60°
Sen50° ⋅ Sec40° − Sen30°
b) 2
c) 4
e) 16
5. Del gráfico, calcular:
K = Cosec2θ + 3
45°
a) 15
d) 12
a
1
b) ab c)
b
ab
m
Sen  7x + 1°  Tg 50°·Cosec(x+13°)·Ctg 40°=1
 2 
·
a) 1°
b) 3°
c) 5°
d) 7°
e) 9°
a) 1
d) 8
a)
te
a
.M
w
w
w
3. Calcular “x” ( agudo), si se cumple:
A=
b
.c
1
1
1
a) b) c)
2
3
4
1
1
d) e)
5
6
4.Calcular:
a
b) 14
e) 11
c) 13
U N F V – C E P R E V I
a) 1
d) 4
b) 2
e) 6
c) 3
10.Calcular “x” ( agudo)
Sen(3x+y+10°)·Sec(2x-y+30°)=2Cos 60°
a) 10°
b) 20°
c) 30°
d) 15°
e) 25°
11.Si:
2Senθ+Cosec θ = 3 ; 0° < θ < 90°
Calcular:
K = 6Cos 2θ + Ctg2θ
a) 2
b) 4
c) 6
d) 8
e) 10
35
TRIGONOMETRÍA
12.De la figura, calcular:
17.Dado un triangulo rectángulo ABC. Si:
Sec A + Ctg C = 5
Calcular:
θ
K = Ctg(θ-15°) + Tg
3
a) 1
d) 4
=
K
2ab
a
b
b) 2
e) 5
15(Co sec C − TgA) + 1
a) l
d) ±2
b) 2
e) 4
c) ±1
18.En la figura, calcular:
K = 8Tg θ – 3
c) 3
θ
13.Si:
Tg x – Sen 30° = 0 ; 0° < x < 90° ^
Cosec y=Tg 60°·Cosec x; 0°<y<90°
Calcular:
37°
a) 1
e) 0
A=Sec45°·Ctgy– Co sec 2 x + Sec60°
a) 3 b) 5 c) 6
d) 7 e) 10
c) 1/2
19.Dado un triángulo ABC, la expresión:
K = a(1+Cos B) + b(1+Cos A)
representa:
a) Área
b) Doble del área
c) Perímetro
d) Doble del perímetro
e) Semiperimetro
te
a
.M
w
c) 3
20.En la figura, calcular: Tg θ
w
15.En la figura: S = Área.
Calcular: Tg θ
6ab
a
w
x
10
Calcular “x”.
a) 1
b) 2
d) 4
e) 5
m
a
ti
ca
1
.c
o
m
14.En la figura: Ctg α = 2 ^ Ctg θ = 3
b) 2
e) –1
b
a) 2 2 +1 b) 2( 2 +1)c) 2 2 +3
d) 2( 2 +2) e) 2 2 +5
S
θ
a) 1
d) 1/5
45° 2S
b) 2
e) 4
c) 5
16.En un triangulo ABC (recto en B) se
cumple:
4Tg A · Ctg C =Sen A · Sec C
Calcular:
a) 3
d) 9
36
K = 5 · Cosec A + Tg C
b) 5
c) 7
e) 11
1. c
6. d
11. c
16. c
2. a
7. d
12. b
17. b
CLAVES I
3. c
4. d
8. a
9. e
13. d 14. b
18. d 19. c
5. c
10. a
15. d
20. c
Problemas II
1.Si:
Sen x
Cos y
7
2
= 0,333… ^
= 0,2
(“x” e “y” son ángulos agudos)
U N F V – C E P R E V I
TRIGONOMETRÍA
Calcular:
H=
6. Hallar “Sen
TanY ⋅ CotX + CosX ⋅ SecY
CscY ⋅ CscX − CotY ⋅ CotX
7
2
1
b) c)
2
7
7
d) 7
e) 7
16
a)
2. En un triángulo rectángulo ABC (recto
en A). Hallar “Tg C”, si se verifica la
relación:
a) 1
d) 1/2
9
α
24
7
25
b)
c)
25 24
7
25
7
d)
e)
24
25
a)
CscB − SenB
=8
SecB − CosB
b) 2
e) 1/8
α
” del gráfico siguiente:
2
c) 8
3. Calcular el perímetro de un triángulo
rectángulo, cuya área es 7,5 cm², si el
valor de la tangente trigonométrica de
uno de sus ángulo agudos es 5/12.
a) 12 cm
b) 13 cm c) 15 cm
d) 24 cm
e) 30cm
7. Encontrar “x” a partir de la relación:
4. La altura desigual de un triángulo
isósceles mide 15 cm; siendo su
perímetro 50 cm, calcular el coseno
de uno de sus ángulos iguales.
8. Hallar “x” e “y” del sistema:
Sec(4x+y)–Csc(y–x) = 0
...(i)
Tan(5x − y)
= 1
...(ii)
Cot(2y + x)
Sen(3x − 20°) ⋅ Csc40° Cos(2x + 30°) ⋅ Sec50°
=
Tan(10° + x)
Cot(80° − x)
5. De la figura mostrada, calcular:
CD
W = 2Tan φ – Tan 2 φ , si:
= BD
3
B
D
o
.c
ti
ca
1
c) 18°
a
m
te
a
.M
w
w
w
15
17
17
b)
c)
a)
17
15
8
8
8
d)
e)
17
15
b) 8°
e) 20°
m
a) 16°
d) 9°
a) x = 5° ; y = 35°
b) x = 10° ; y = 30°
c) x = 30° ; y = 10°
d) x = 15° ; y = 25°
e) x = 25° ; y = 15°
π
C
D
9. Si: 2A+2B = rad y
+ = 25g.
3
2 2
Calcular:
M= Sen 3A – Cot 2D + Tan 2C – Cos 3B
a) 0
b) 1
c) 2
d) 4
e) F.D.
10.Reducir:
A
C
H
a) 0
b) 2 d) 2 2 e) –2 2
c) – 2
U N F V – C E P R E V I
H=
Sen5 15° ⋅ Csc 3 15° + Cos6 15° ⋅ Sec 4 15°
3
a) 1
c) 2sen215°
e) 1/2
3
Tan2 15° ⋅ Cot 2 15°
b) 2
d) 2Cos215°
37
TRIGONOMETRÍA
11.Si:
[Sen2φ]Secφ=[Csc3φ]–Cos φ ; 0°< φ <90°.
Calcular el valor de:
P = [Tan3φ]Cot²φ
a) 4 8 b)
1
d) 8
1
4
16.Del gráfico, calcular “Cos φ”.
45°
φ
c) 4
e) 8
a)
12.Si: Ctg[2x+10g] · Ctg[11° + 5x] = 1 ;
halle “x”.
=
Q
3π
Sen 30° + 0,5Csc 60° + 6 Sec  
3
4π
2π
Cot   + Sec   + 3Tan 37° ⋅ Tan 53°
6
4
6
3
Tanθ − Cotθ
B
a
ti
ca
1
.c
o
m
127°
m
w
−2
3
3
17.En el triángulo ABC mostrado, si:
5AB = 6BC; calcular el valor de:
te
.M
a
Q=
4
w
2
w
14.Calcular el valor de:
b) 2 c)
d) 3 e)
π
π
π
radb)
radc)
rad
20
18
10
π
π
d) rade) rad
9
2
a)
13.Siendo “φ" y "β" las medidas de dos
ángulos agudos y complementarios
indicar la alternativa incorrecta:
Senφ
=1
a)
Cosβ
b) Cos β – Sen φ = 0
c) Sen φ · Sec β = 1
d) Tg β· Ctg φ = 1
e) Cos φ · Csc β – 1 = 0
2
2 A
C
6
5
5
d) – 6
a)
b) –
6
5
c)
5
6
e) 1
18.Encontrar “Tan α” de la semicircunferencia de centro “O” mostrada
en la figura.
1 c) 1
14
12
a) 1
b)
d) 12
e) 14
15.En un triángulo ABC, si:
60°
 5π 
A=
 rad ; B = 50g y AB = 18
 12 
α
O
Calcular el lado “b”.
a) 2 2 b) 3 2 c) 6 + 2
a)
1
3
3
b)
c)
7
7
8
d) 2 2 e) 2 3
d)
7 3
8 3
e)
3
3
38
U N F V – C E P R E V I
TRIGONOMETRÍA
19.En la figura, calcular: “Cot φ"
20.De la figura mostrada, hallar:
M = 32Tan β + 3Cot β
37°
45°
φ
3
7
7
d) 4
a)
37°
b)
4
7
c)
7
3
60°
a) 4 3 d) 24
e) 7
2. b
7. a
12. b
17. d
c) 8 3
CLAVES II
3. c
4. d
8. b
9. a
13. d 14. b
18. b 19. c
5. c
10. a
15. e
20. d
w
w
w
.M
a
te
m
a
ti
ca
1
.c
o
m
1. a
6. e
11. d
16. c
b) 12
e) 35
β
U N F V – C E P R E V I
39