Diseño factorial 2 x 2

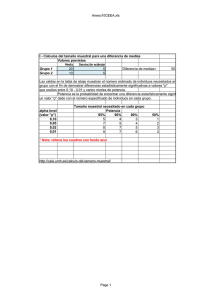
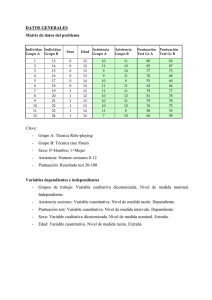
Diseño factorial 2 x 2
Supuesto: El niño superdotado
Tal y como señaló Terman (1925), como grupo los niños bien dotados tienen un desarrollo precoz en áreas como el lenguaje, la
lectura, la escritura y el procesamiento de la información. Destaca la facilidad que tienen para aprender a leer sin ningún tipo de
instrucción o con poca ayuda. El 45% de los niños del grupo de California aprendió a leer antes de entrar en la escuela. Los resultados
de las investigaciones también indican que existe una relación directa entre la eminencia y el nivel socioeconómico y educativo de los
padres.
Dos psicólogos dedicados al área educativa deciden emprender una investigación cuyo objetivo principal radica en el análisis de la
relación entre: inteligencia y nivel educativo de los padres respecto a la variable de rendimiento escolar, con objeto de corroborar los
resultados aportados por la literatura. Como primer paso realizan un diagnóstico de inteligencia a los niños que cursan 5º de
Enseñanza Primaria en los siete Centros Escolares de su zona, recogiendo además el nivel educativo de los padres. La inteligencia la
miden con la Escala de Inteligencia de Wechsler para niños revisada (WISC-R, Wechsler, 1993) y la educación de los padres se
codificada en dos niveles en función de si ambos padres poseen el título de Graduado Escolar o no. A partir de las puntuaciones en
inteligencia se dicotomizó la muestra tomando como punto de corte la puntuación media. A partir de estas dos categorías a cada uno
de los alumnos se le asignó a una de las cuatro posibles combinaciones de los dos grupos de inteligencia y nivel educativo de los
padres; una vez todos los alumnos estaban asignados a uno de los cuatro grupos se extrajeron dos de cada uno mediante un
procedimiento aleatorio. Para cada uno de los ocho sujetos seleccionados se registraron las calificaciones de las asignaturas de
matemáticas, lenguaje y ciencias sociales y se calculó la puntuación media.
Cuestionario
1.
¿Cuál es la variable dependiente del experimento?
a)
b)
c)
d)
e)
2.
Los factores del diseño son:
a)
b)
c)
d)
e)
3.
el nivel socioeconómico medio de la familia
el rendimiento escolar medio
la media de inteligencia
el nivel educativo medio de los padres
no se puede responder a esta pregunta
nivel de inteligencia y nivel socioeconómico de la familia
tipo de familia y nivel de estudios de los padres
nivel de inteligencia y nivel de estudios de los padres
nivel de estudios de los padres y nivel socioeconómico familiar
no se puede responder a esta pregunta
¿Cuál es la hipótesis experimental?
a)
b)
c)
d)
la única variable relevante en relación al rendimiento escolar es el nivel socioeconómico de la familia
la única variable relevante en relación al rendimiento escolar es el nivel de inteligencia del niño
la única variable importante en relación al rendimiento escolar es el nivel de educación de los padres
los niños con una puntuación superior a la media de inteligencia y con padres con estudios superiores al Graduado Escolar tendrán un
rendimiento escolar más satisfactorio
e) no se puede responder a esta pregunta
4.
El planteamiento de la hipótesis experimental indica un efecto:
a)
b)
c)
d)
e)
5.
Cuando la distancia entre las medias es constante:
a)
b)
c)
d)
e)
6.
de interacción entre tres factores
de interacción entre cuatro factores
de interacción entre dos factores
principal de cada uno de los dos factores
efectos aditivos
el efecto de interacción está presente
el efecto de interacción no está presente
el efecto de interacción es estadísticamente significativo
es necesario interpretar el efecto de interacción y no los efectos principales
no se puede responder a esta pregunta
En comparación con el diseño unifactorial, el diseño factorial supone en general:
a)
b)
c)
d)
e)
el aumento del error
la igualdad del error
la eliminación del error
la reducción del error
no se puede responder a esta pregunta
1
7.
Cuando el efecto de interacción en un diseño 2 x 2 es estadísticamente significativo:
a)
b)
c)
d)
hay que interpretar un sólo efecto principal pero nunca los dos
hay que interpretar únicamente el efecto de interacción
hay que interpretar únicamente los dos efectos principales
hay que interpretar únicamente el efecto de interacción dividiendo su suma de cuadrados por la media de las sumas de cuadrados de los dos
efectos principales
e) no se puede responder a esta pregunta
8.
El efecto de interacción es una medida:
a)
b)
c)
d)
e)
9.
de la aditividad de los efectos principales
de la desviación de los efectos principales
de la concurrencia de los efectos principales
de la no aditividad de los efectos principales
no se puede responder a esta pregunta
El procedimiento de los efectos simples permite analizar:
a)
b)
c)
d)
e)
el efecto de los factores dobles
el efecto de los factores simples
el efecto de los factores principales
el efecto de la interacción
no se puede responder a esta pregunta
10. La representación gráfica de las puntuaciones medias de las condiciones experimentales:
a)
b)
c)
d)
e)
ayuda a la comprensión de los efectos
únicamente puede realizarse para los efectos que resultan estadísticamente significativos
permite rechazar o aceptar la hipótesis nula según el nivel alfa fijado a priori
es muy útil cuando el alfa alcanzado a posteriori supera al nivel fijado a priori
no se puede responder a esta pregunta
Ejercicios: completar la tabla de ANOVA, analizar el efecto de interacción si es
estadísticamente significativo. Ejecutar con el SPSS. Redactar los resultados.
Tener en cuenta que:
Por efecto principal debemos entender el que produce
una variable independiente en un diseño factorial, sin
considerar la presencia de otras variables
independientes en el mismo diseño. Es importante
tener en cuenta de que no debe tomarse aquí el término
principal como equivalente a "más importante", sino
como sinónimo de "fundamental", "básico" o
"elemental", esto es, que sirve de base o fundamento a
otros. El motivo de esto es que cuando en un mismo
diseño
un
efecto
principal
estadísticamente
significativo participa además de una interacción
estadísticamente significativa, no es posible interpretar
aquél sin conocimiento de ésta.
Por efecto de interacción entre dos variables
independientes debemos entender que el efecto de una
de ellas es distinto en distintos niveles de la otra
variable.
2
1.
Complete la tabla resumen del análisis de la varianza.
Tabla Diseño factorial 2  2 entre _____________________________________________________
Fuente
SC
gl
A
B
AB
Error
Total
2.
MC
Razón F
p
0.050
0.050
0.050
Ftablas (alfa,glefecto, glerror )
Ftablas (alfa,glefecto, glerror )=
Represente gráficamente el efecto de interacción.
b1
b2
30
25
20
15
10
5
a1
3.
a2
Determine el rango crítico entre pares de medias.
q(, a · b, gl )
cij²
– –
|Yg – Yh| 
MCerror a b
2
i=1, j=1 nij
q(0.05, 4, 4)
– –
1² -1² 0² 0²
|Yg – Yh| 
MCerror  2 + 2 + 2 + 2  
error
2
3
^²


5.757
7.500 · 1.000 = 4.071 · 2.739 = 11.148
2
_________________________________________________________________________________________
_________________________________________________________________________________________
_________________________________________________________________________________________
_________________________________________________________________________________________
_________________________________________________________________________________________
_________________________________________________________________________________________
_________________________________________________________________________________________
_________________________________________________________________________________________
_________________________________________________________________________________________
_________________________________________________________________________________________
_________________________________________________________________________________________
Recordar:
4