Señalar variables dependientes e independientes

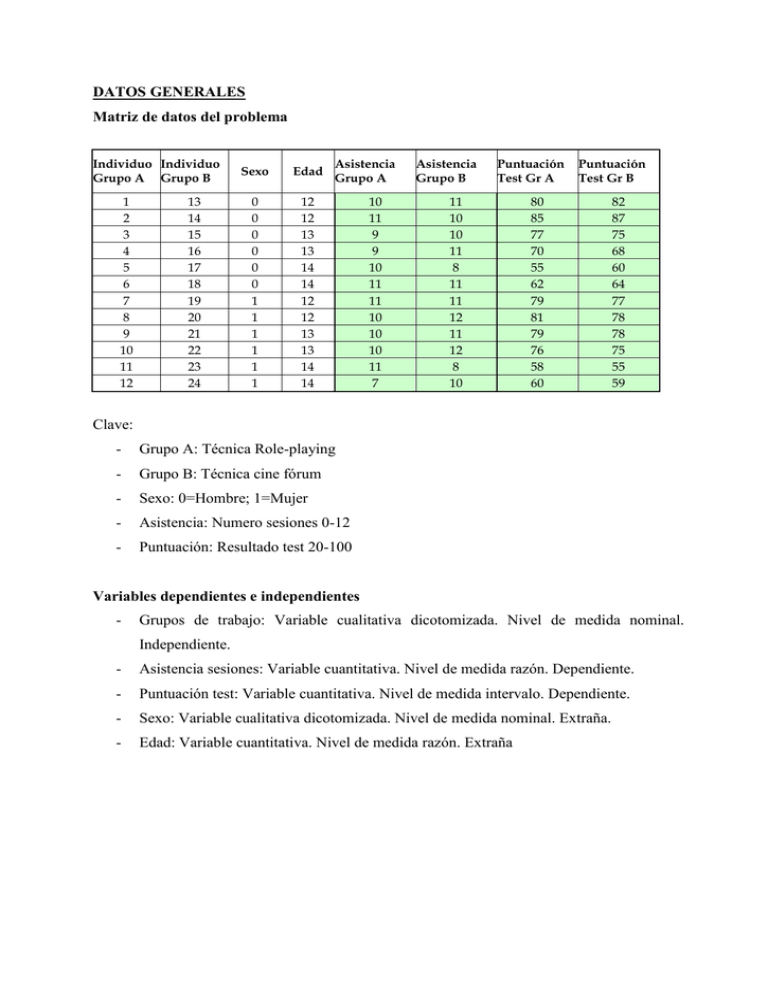
DATOS GENERALES
Matriz de datos del problema
Individuo Individuo
Grupo A Grupo B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
Sexo
Edad
0
0
0
0
0
0
1
1
1
1
1
1
12
12
13
13
14
14
12
12
13
13
14
14
Asistencia
Grupo A
10
11
9
9
10
11
11
10
10
10
11
7
Asistencia
Grupo B
Puntuación
Test Gr A
11
10
10
11
8
11
11
12
11
12
8
10
Puntuación
Test Gr B
80
85
77
70
55
62
79
81
79
76
58
60
82
87
75
68
60
64
77
78
78
75
55
59
Clave:
-
Grupo A: Técnica Role-playing
-
Grupo B: Técnica cine fórum
-
Sexo: 0=Hombre; 1=Mujer
-
Asistencia: Numero sesiones 0-12
-
Puntuación: Resultado test 20-100
Variables dependientes e independientes
-
Grupos de trabajo: Variable cualitativa dicotomizada. Nivel de medida nominal.
Independiente.
-
Asistencia sesiones: Variable cuantitativa. Nivel de medida razón. Dependiente.
-
Puntuación test: Variable cuantitativa. Nivel de medida intervalo. Dependiente.
-
Sexo: Variable cualitativa dicotomizada. Nivel de medida nominal. Extraña.
-
Edad: Variable cuantitativa. Nivel de medida razón. Extraña
PROBLEMAS
a) Valorar el interés de los dos grupos por el objeto del programa a partir de los datos
descriptivos.
-
A partir de la matriz de datos del inicio seleccionamos los datos que se nos solicita:
Individuo Individuo Asistencia Asistencia
Grupo A Grupo B Grupo A Grupo B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
SUMA
-
10
11
9
9
10
11
11
10
10
10
11
7
11
10
10
11
8
11
11
12
11
12
8
10
119
125

XA  XA XB  X B X A  X A
1,75
-0,25
-1,25
-0,25
-0,25
0,75
0,75
-0,25
-0,25
-0,25
0,75
-1,25
0,25
0,25
-0,75
0,25
-1,75
0,25
0,25
1,25
0,25
1,25
-0,75
-0,75
 X
2
A
 XA
3,06
0,06
1,56
0,06
0,06
0,56
0,56
0,06
0,06
0,06
0,56
1,56
0,06
0,06
0,56
0,06
3,06
0,06
0,06
1,56
0,06
1,56
0,56
0,56
14,92
18,92

2
Cálculo de los datos:
o Medias: X
A

119
125
 9,92 y X B 
 10,42
12
12
o Desviaciones típicas: S A 
14,92
 1,16 y S B 
12  1
18,92
 1,31
12  1
o Modas: Mo A  10 y MoB  11
o Medianas:
-
Md A  10 y Md B  11
Interpretación de los datos
En el grupo B la moda es un punto mayor y la media también es mayor en medio punto,
lo que nos dice que este grupo ha obtenido una mayor asistencia.
La desviación típica en dicho grupo es apenas algo mayor, lo cual da idea de una menor
homogeneidad, si bien en una magnitud en que no podemos decir que sea muy
significativa.
En cualquier caso sería interesante el estudio de la variable asistencia comparándola
con las variables sexo y edad, para poder ver si estas variables extrañas tienen alguna
influencia estadísticamente significativa con la asistencia.
b) Decidir, en términos estadísticos, si existen efectos diferenciales entre el sistema de
“role-playing” y el de cine forum, a un nivel reconocido en la comunidad científica
1.-Establecer hipótesis estadística
-
H 0 : No existen efectos diferenciales estadísticamente significativos entre el grupo A y
el grupo B en relación a los resultados del cuestionario sobre xenofobia. H 0 :  A   B
-
H 1 : La diferencia de resultados en el cuestionario sobre xenofobia es estadísticamente
significativa, siendo mayor en el grupo B. H1 :  A   B
2.-Seleccionar la prueba estadística
-
Vemos que la prueba debe ser paramétrica debido a que
o Normalidad: Asumimos que la población tiene una distribución normal, ya que
no se indica lo contrario.
o Igualdad de varianza: Se cumple dado que los sujetos pertenecen a la misma
población
o Independencia de los datos: Se da al formarse los grupos aleatoriamente
o Además la variable dependiente a estudiar es cuantitativa con un nivel de
medida de intervalo y los grupos están relacionados, dado que hemos
determinado que cada grupo esté compuesto del mismo número de individuos
de cada sexo y edades.
-
Aplicamos la diferencia de medias entre poblaciones relacionadas, t de Student, debido
a que los grupos constan de menos de 30 individuos.
3.-Resolución de la prueba estadística
-
Encuentro el valor empírico de t a través de la formula de la t de Student:
t
d
Sd / n
donde: d = media de la diferencia de puntuaciones en las parejas de ambos grupos
S d = desviación típica de las diferencias
n = número de parejas
-
trabajando sobre la matriz de datos obtengo:
Individuo Individuo Puntuación Puntuación
Grupo A Grupo B
Test Gr A Test Gr B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
80
85
77
70
55
62
79
81
79
76
58
60
82
87
75
68
60
64
77
78
78
75
55
59
SUMAS
d
d d
d  d 
-2
-2
2
2
-5
-2
2
3
1
1
3
1
-2,33
-2,33
1,67
1,67
-5,33
-2,33
1,67
2,67
0,67
0,67
2,67
0,67
5,44
5,44
2,78
2,78
28,44
5,44
2,78
7,11
0,44
0,44
7,11
0,44
4
o con lo que d 
o así t empírica 
2
68,67
4
68,67
 0,33 y S d 
 6,24  2,50
12
12  1
0,33
2,50 / 12

0,33
= 0,46
0,72
-
A continuación hallo el valor teórico de t a traves de las tablas:
o Establezco el nivel de confianza. Al no venir indicado asumimos un nivel de
confianza del 95%, usual en las investigaciones científicas, con lo cual  =0,05
o Sabemos que el contraste es de una cola ya que postulamos H1 :  A   B
o El grado de libertad son de n-1 = 11
o En consecuencia según las tablas t teórica = 1,796
-
Comparamos los valores teórico y empírico de t e interpretamos el resultado:
o Vemos que t empírico  t teórico con lo cual rechazamos H 1 y aceptamos H 0
o Esto quiere decir que el resultado de nuestra investigación concluye que no
existen efectos diferenciales estadísticamente significativos entre el grupo A
y el grupo B en relación a los resultados del cuestionario sobre xenofobia