Serie 1.

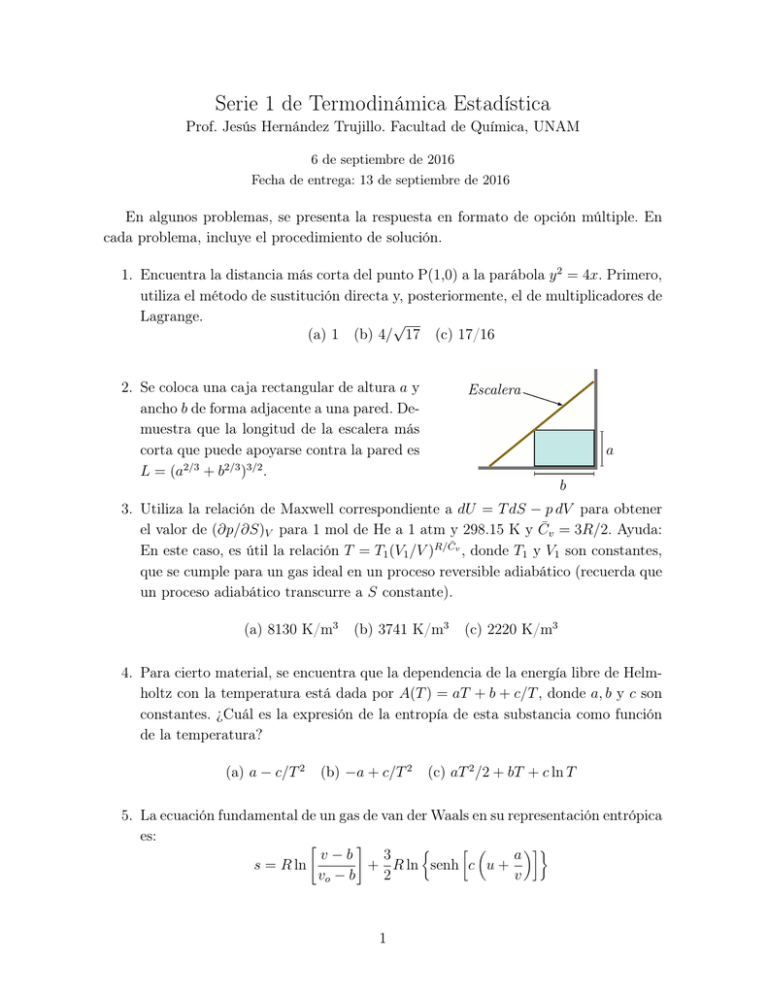
Serie 1 de Termodinámica Estadística
Prof. Jesús Hernández Trujillo. Facultad de Química, UNAM
6 de septiembre de 2016
Fecha de entrega: 13 de septiembre de 2016
En algunos problemas, se presenta la respuesta en formato de opción múltiple. En
cada problema, incluye el procedimiento de solución.
1. Encuentra la distancia más corta del punto P(1,0) a la parábola y 2 = 4x. Primero,
utiliza el método de sustitución directa y, posteriormente, el de multiplicadores de
Lagrange.
√
(a) 1 (b) 4/ 17 (c) 17/16
2. Se coloca una caja rectangular de altura a y
ancho b de forma adjacente a una pared. Demuestra que la longitud de la escalera más
corta que puede apoyarse contra la pared es
L = (a2/3 + b2/3 )3/2 .
Escalera
a
b
3. Utiliza la relación de Maxwell correspondiente a dU = T dS − p dV para obtener
el valor de (∂p/∂S)V para 1 mol de He a 1 atm y 298.15 K y C̄v = 3R/2. Ayuda:
En este caso, es útil la relación T = T1 (V1 /V )R/C̄v , donde T1 y V1 son constantes,
que se cumple para un gas ideal en un proceso reversible adiabático (recuerda que
un proceso adiabático transcurre a S constante).
(a) 8130 K/m3
(b) 3741 K/m3
(c) 2220 K/m3
4. Para cierto material, se encuentra que la dependencia de la energía libre de Helmholtz con la temperatura está dada por A(T ) = aT + b + c/T , donde a, b y c son
constantes. ¿Cuál es la expresión de la entropía de esta substancia como función
de la temperatura?
(a) a − c/T 2
(b) −a + c/T 2
(c) aT 2 /2 + bT + c ln T
5. La ecuación fundamental de un gas de van der Waals en su representación entrópica
es:
"
#
v−b
3
a
s = R ln
+ R ln senh c u +
vo − b
2
v
1
donde s, u y v son la entropía, la energía interna y el volumen molar, respectivamente. Además, R, a, b, c y v0 son constantes. Obtén las ecuaciones de estado
para demostrar que
p=
a
RT
− 2
v−b v
6. Considera la siguiente ecuación fundamental U (S, V, N ) = k S 3 /(N V ), donde k es
una constante. Mediante la transformada de Legendre, encuentra la expresión de
la energía libre de Gibbs, G = G(T, p, N ).
q
(a) − N 2 pT 3 /(9k) (b) −2N pT 3 /(3) (c) −N T 3 /(27kp)
7. La nitrogenasa es una enzima que convierte N2 en NH3 que contiene un cúmulo
Fe4 S4 formando un cubo de arista a = 3 Å. Utiliza el modelo de una partícula en
una caja de potencial infinito cúbica y calcula
Fe
S
la longitud de onda de la radiación electromaga
S
Fe
nética para llevar a cabo la transición electróS
Fe
nica de más baja energía. Supón que el número
total de electrones de valencia es 20.
Fe
S
(a) 294 nm
(b) 155 nm
(c) 437 nm
8. Las siguientes líneas (en cm−1 ) del espectro vibración-rotación corresponden a la
banda fundamental de la molécula de HCl.
2821.43
2843.56
2865.09
2906.25
2925.78
2944.89
Calcula la longitud de enlace y la constante de fuerza de la molécula.
(a) 0.13 nm, 0.048 N/m
(b) 1.29 nm, 27 N/m
2
(c) 1.30 Å, 477 N/m