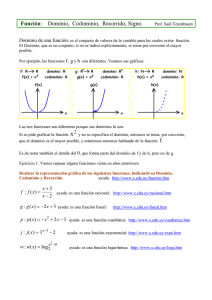
59. Analiza funciones exponenciales y logarítmicas

INSTITUTO TECNICO CENTRAL
ESCUELA TECNOLÓGICA – INSTITUCIÓN UNIVERSITARIA
INSTITUTO DE BACHILLERATO TÉCNICO INDUSTRIAL
PLANEACIÓN BIMESTRAL
PERIODO: Cuarto
ASIGNATURA: Matemáticas
GRADO:9º
LOGROS
59. Analiza funciones exponenciales y logarítmicas
60. Resuelve ecuaciones exponenciales y logarítmicas
61. Soluciona problemas aplicando las características fundamentales de
las progresiones aritméticas y geométricas
62. Resuelve situaciones problemas donde intervienen los conceptos
fundamentales de la probabilidad y Estadística.
SEMANA
1.
CONTENIDOS
COMPETENCIAS
Función exponencial.
Resuelve
y
formula
problemas
aplicando las características de las
funciones exponenciales.
Concepto
2.
3.
4.
Representación
Grafica con destreza la función
gráfica.
exponencial
Ecuaciones
Resuelve y formula problemas que
exponenciales.
involucren ecuaciones exponenciales.
Función logarítmica
Aplica el concepto de función
logarítmica en la solución de
problemas.
5.
Reconoce el significado de las
propiedades de las progresiones y las
aplica en soluciones concretas.
Sucesiones y
progresiones
6.
Progresiones
Identifica eficientemente la forma de
aritméticas y
resolver problemas sobre
geométricas.
progresiones aritméticas y
geométricas.
7.
Interpreta
percentiles
en
una
distribución de datos e Interpreta las
medidas
de
dispersión
y
las
frecuencias.
Estadística.
90
8.
Probabilidad
Comprende las técnicas de conteo,
reconoce la diferencia entre
permutación y combinación, define las
diferentes clases de eventos.
9.
NIVELACIÓN /
Adquiere la capacidad para interpretar,
10.
NIVELACIÓN /
argumentar y
RECUPERACIÓN
proponer soluciones a diversos
problemas que involucran contenidos
FORTALEZAS
64.
Analiza
las
funciones
exponenciales
y
logarítmicas
eficientemente.
DEBILIDADES
69. Confunde las
diversas gráficas y
principales
características de
funciones
exponenciales y
logarítmicas.
RECOMENDACIONES
73. Realizar con mayor
precisión y orden los
ejercicios propuestos.
65.
Resuelve
ecuaciones
exponenciales
y
logarítmicas
correctamente
70.Presenta
dificultades en la
solución de
ecuaciones
exponenciales y
logarítmicas
71.
Tiene
dificultades
para
identificar
las
progresiones
aritméticas
y
geométricas.
74. Realizar problemas
relacionados con
las
progresiones
aritméticas y geométricas,
y realizar problemas.
66. Soluciona
problemas aplicando
las características
fundamentales de las
progresiones
aritméticas y
geométricas en forma
clara y precisa
67. Resuelve
problemas donde
intervienen los
conceptos
fundamentales de la
probabilidad y
Estadística
75. cumplir con las
actividades de
recuperación asignadas.
76. Resolver ejercicios y
problemas relacionados
con los conceptos
fundamentales de
estadística y probabilidad
91
FUNCIÓN EXPONENCIAL
La función exponencial viene dada por:
exponente x es una variable.
f(x) =
a X , donde a es un número y el
El dominio de la función es R, (−∞, ∞) o se el conjunto de los números reales, por eso la
función puede tomar valores en todo el eje de las x.
El rango de la función es R +, (0, ∞) o sea el conjunto de los números reales positivos, por
eso la curva toma valores solamente por encima del eje de las x.
Ejercicio: Dibujar la gráfica de la función f(x) = 2 X .
2 −3 =
1
8
21 = 2
X
Y
2−2 =
1
4
2−1 =
22 = 4
-3
1
8
1
2
20 = 1
23 = 8
-2
1
4
-1
1
2
0
1
Con estos datos dibuje la gráfica en su cuaderno.
Ejercicio:
1) Dibujar la gráfica de f(x) = 2 − X
2) Dibujar la gráfica de f(x) = e X
E es un número irracional cuyo valor aproximado es: 2.71828
Germán Giraldo Giraldo
92
1
2
2
4
3
8
Propiedad fundamental de los exponentes:
am = an
Esto se cumple si y solamente si
Ejemplo: 212 = 23 X
m = n
entonces 12 = 3x ⇒ x = 4
Ejercicios:
3) 43x+5 = 32x-2
4) (0, 25) x+1 = (0,125) x-1
5) 640,75x+1 = 0,250,25x-1
6) a5x-4 · ax-7 = 1
7) b3x-1 . b2x-3 = bx+1 · b2x-5
8)
9)
10) 102x-1 - 10x = 0
11) 5·2x-2 - 3·2x-3 = 14
12) 32-x = 3
13) 42x+1 = (0,5)3x+5
14) 2x-1 + 2x + 2x+1 = 7.
15) ex - 5e-x + 4e-3x =0.
16) 31− x =
17) 5x+1 + 5x = 750
18) 4x - 2x = 2
2
19) 9x - 2·3x+2 + 81 =0.
Germán Giraldo Giraldo
93
1
27
Función logarítmica
F(x) = logax
En este caso a es un número.
que f(x) = y; por tanto podemos escribir y = logax
Ya sabemos
De la forma logarítmica a la exponencial:
⇔ ay
y = logax
= x
log28 = 3
Ejemplo:
⇔
23 = 8
Ejercicios:
Pasar de la forma logarítmica a la exponencial, ó al contrario según el caso:
19) log25 5 =
1
2
20) log2
1
= -2
4
21) log3 27 = 3
22) log366 =
1
2
23) log3
1
= -2
9
24) 72 = 49
25)
26) 5 −1 =
9 = 3
1
5
27) 4− 2 =
1
16
Ejemplo: Escribir en forma logarítmica: 8 = 22y (Para ello expresamos cada miembro en
la misma base 2)
23 = 22y y si queremos resolver esta ecuación igualamos los exponentes, ya que las bases
son iguales:
3 = 2y
⇒
y =
3
2
Germán Giraldo Giraldo
94
Gráfica de la función logarítmica
Y = loga x
El dominio de la función es el conjunto de los números reales positivos:
D[f(x)] = R+; (0, ∞ )
El rango de la función es el conjunto de todos los números reales como lo vamos a apreciar
en la gráfica.
R[f(x)] = R; ( ∞ , ∞ )
Ejercicio: Dibujar la gráfica de la función y = log2 x
X
Y
1
8
-3
1
4
-2
1
2
-1
1
2
4
8
0
1
2
3
Con estos datos dibuje la gráfica en su cuaderno.
Ejercicios:
Encuentre cada logaritmo:
28) log10 105 = ___
29) log5 53 = ___
30) log22-4 = ___
31) log10 10-8 = ___
32) log10 0.0001 = ___
33) log3 81= ___
Halle el valor de x en cada caso:
34) log3 x = 4
35) log4 64 =x
36) logx 32 = 5
37) log8 x = 3
38) logx 125 =3
39) log10 x = 5
Germán Giraldo Giraldo
95
Propiedades de las funciones logarítmicas
Las funciones logarítmicas son inversas de las funciones exponenciales. De este hecho se
derivan las propiedades de la función logarítmica.
Sean M y N dos números reales positivos y a ≠ 0. Podemos enunciar las propiedades de la
siguiente manera:
1) loga ap = p
3) loga
2) loga MN = loga M + loga N
M
= loga M - loga N
N
4) loga Mp = p loga M
5) loga 1 = 0
Ejercicios:
Aplicar las propiedades en los siguientes casos:
40) log10 106 =
41) loga 5x =
42) loga
x
=
4
43) loga m6 =
44) loga
xy
=
mn
45) loga
46) log a
m7
n
=
3
4
2
⎛ x ⎞3
48) loga ⎜ ⎟
⎝ y⎠
3
( pq ) 4
⎛ ⎞
47) loga ⎜ m ⎟
⎝ np ⎠
⎛ 12
m
49) loga ⎜ 3
⎜n
⎜
⎝
Germán Giraldo Giraldo
96
⎞
⎟
⎟
⎟
⎠
=
Escriba cada expresión con un solo logaritmo con el coeficiente 1:
50) loga M + loga N
51) loga B + loga C + loga D
52) loga x3 + loga y3 - loga z3
53)
1
( 3log a m + 4 log a n )
3
Exprese como suma de logaritmos y use exponentes si es el caso en los siguientes
ejercicios:
54) loge 10
55) loge 15
56) loge 75
57) loge 45
Aplique las propiedades logarítmicas hasta donde pueda, en los siguientes casos:
3
58) loga x y
60) loga
4
4
59) log
a 5
m 2 n3
p
⎛ m6 ⎞
⎜ 4 5⎟
⎝n p ⎠
3
3
61) loga
m
n p3
2
3
2
log a 4 − log a 8 + 2 log a 2 = log a x
2
3
1
63) Hallar x, tal que: 3 loga 2 +
loga 25 - loga 20 = logax
2
62) Hallar x tal que
64) Despejar y en: loga y – loga m + kt = 0 en forma exponencial sin logaritmos.
65) Despejar x en: loge x - loge 100 = -0,08t en forma exponencial sin logaritmos.
Hallar el valor de x en las siguientes ecuaciones:
66) 3x = 23
67) 105x-2 = 348
68) 103X+1 = 92
69) 3-X = 0,074
Germán Giraldo Giraldo
97
Escribe cada igualdad ó ecuación exponencial en la forma logarítmica y viceversa:
1) 23 = 8
4) log10 0.01 = -2
5) ln 2 = 0.6931...
6) ln 0.5 = -0.6931...
Halla el valor de x:
7) log10 1000 = x
9) log3 x = -1
10) logx 27 = 3
12) log3 x + log3 (x - 2) = 1
13) x - 3 = log2 32
14) x2 - x = log5 25
Germán Giraldo Giraldo
98
Dibuja la gráfica de:
15) f(x) = 3x
16) y = 3-x
Usa las propiedades de los logaritmos para escribir cada expresión dada como una suma,
diferencia o múltiplo de logaritmos.
17) log2 xyz
22) ln 3e2
Escribe cada expresión con un único logaritmo:
23) log3 (x - 2) - log3 (x + 2)
24) 3 ln x + 2 ln y - 4 ln z
25) 2[ln x - ln (x + 1) - ln (x - 1)]
Germán Giraldo Giraldo
99
ECUACIONES LOGARÍTMICAS
Ejemplos:
1. Log3 (2x + 1) = 2
2. Log25 x =
3
2
3
2x + 1 = 32
x = 25 2
x =
2x= 9 – 1
253
x = 53
x = 125
x=4
3. Log3 ( x + 2 ) + Log3 ( x − 4 ) = 3
LOg3 ⎡⎣( x + 2 )( x − 4 ) ⎤⎦ = 3
( x + 2 )( x − 4 ) = 33
x 2 − 4 x + 2 x − 8 = 27
x 2 − 2 x − 35 = 0
x1 = 7
4. Log a x + Log a 6 =
2
1
Log a 8 + Log a 9
3
2
2
Log a x + Log a 6 = Log a 8 3 + Log a 9
Log a ( x .6 ) = Log a 3 82 + Log a 3
Log a ( x .6 ) = Log a 22 + Log a 3
Log a ( x .6 ) = Log a ( 4 × 3)
x2 = − 5
6 x = 12
x= 2
GGG
100
5. Log
Log
( 2)
( )
2
2
x + Log
( 2)
( x) 2 + Log
2 x − 2 Log 2 x = 1
( )
2
2
(2 x) 2 − 2 Log 2 x = 1
2 Log 2 x + Log 2 4 x 2 − 2 Log 2 x = 1
Log 2 4 x 2 = 1
4 x2 = 1
1
2
x= ±
Ejercicios
1. log10 x - log10 (x – 3) = 1
2. log10 (x + 3) - log10 x =1
3. log10 x = log10 24 - log10 8
4. log10 x - log10 (22 – x) = 1
5. log10 x + 4log10 2 - log10 100 = 0
6. loga x + loga 6 =
1
2
loga 8 + loga 9
2
3
7. log10 (x – 15) + log10 x = 2
8. log10 x + log10 50 - log10 100 = 0
9. log
2
x + log 2 2 x − 2log 2 x = 1
11. ln2 x –5ln x = 6
10. log2 x - log8 x = 4
12. log2 (log2 x2) = 2
GGG
Calcula el valor de x en las siguientes ecuaciones:
101
1. Determina el valor de x:
a) logx (1/25) = -2
b) log0,5 2 = x
c) logx 0,25 = 0,5
d) log2 (1/4) = x
2. Desarrolla, utilizando las propiedades de los logaritmos:
a)
b)
c)
3. Expresa como un solo logaritmo:
a)
b) -log a - log b
c) log a + 2 - 2log b
4. Dados log 2 = 0,3 y log 3 = 0,47, calcula:
a) log 81
b) log
c) log 15
d) log 0,75
GGG
e)
102
Determina el valor de x en las siguientes ecuaciones logarítmicas:
1. log(x + 1) + log(x - 1) = 1
2.
3.
4. log5(x2 - 9) - log5(x + 3) = 1
5. log(x + 2) + log(x + 3) = log 2
6. log x - log(x - a) = log(x - a) - log(x + a)
7.
8.
2. Desarrolla, aplicando las propiedades de los logaritmos. Transforma a la forma
exponencial y calcula x.
a) log2x = 4
b) loxx81 = 4
c) logx(1/8) = 3
d) log1/2x = -3
e) log264 = x
f) log4x = 3/2
GGG
Progresiones aritméticas.
Una sucesión de números reales es un conjunto ordenado de infinitos números reales a 1,
a2, a3, a4, a5,..., an,... Cada uno de los números reales se llama término de la sucesión.
103
El conjunto ordenado de números impares 3, 5, 7, 9, 11, 13,... es una sucesión de números
reales.
Al término: an = 3 + 2(n-1) se le llama término general; n es el puesto del término
dentro de la sucesión. Para 7 n es 3.
Sin embargo, no todas las sucesiones tienen término general. Por ejemplo, en la importante
sucesión de los números primos: 2, 3, 5, 7, 11, 13, 17, 19, 23,... no hay ninguna fórmula
que exprese el término general.
Consideremos la sucesión de término general an = 3n + 2
an : 5, 8, 11, 14, 17, 20,...
Observamos que cada término de la sucesión es igual que el anterior más 3. Se dice que la
sucesión an es una progresión aritmética y que d = 3 es la diferencia de la progresión.
Una progresión aritmética es una sucesión de números tales que cada uno de ellos (salvo el
primero) es igual al anterior más un número fijo llamado diferencia que se representa por d.
En la progresión anterior a1 = 5, a2 = 8 y d = 8 - 5 = 3.
En ocasiones nos referimos a la progresión formada por los n primeros términos de la
progresión; en este caso se trata de una progresión aritmética limitada.
Son progresiones aritméticas:
•
•
•
Los múltiplos de 2 o números pares: 2, 4, 6, 8, 10... La diferencia es d = 2.
Los múltiplos de 3: 3, 6, 9, 12, 15... La diferencia es d = 3.
Los múltiplos de a: a, 2a, 3a, 4a, 5a... La diferencia es d = a.
GGG
104
Término general.
Fijémonos en la progresión aritmética ilimitada a1, a2, a3, a4, a5,..., an,... Según la
definición, cada término es igual al anterior más la diferencia.
a2 = a1 + d
a3 = a2 + d = a1 + d + d = a1 + 2d
a4 = a3 + d = a1 + 2d + d = a1 + 3d
Generalizando este proceso se obtiene el término general:
an = a1 + (n – 1).d
Ejemplos:
•
El término general de la progresión aritmética 5, 8, 11, 14... es:
an = 5 + (n - 1) . 3 = 5 + 3n - 3 = 3n + 2
•
El término general de una progresión aritmética en la que a1 = 13 y d = 2 es:
an = 13 + (n - 1) · 2 = 13 + 2n - 2 = 2n + 11
•
Vamos a hallar el primer término de una progresión aritmética sabiendo que a11 =
35 y d = 4.
Para ello escribimos a11 = a1 + (11 - 1) · 4, es decir, 35 = a1 + 40, de donde a1 = 35 40 = -5
Se puede conseguir otra expresión para el término general en función de otro término
cualquiera, en lugar del primer término. Como an = a1 + (n - 1) · d y ak = a1 + (k - 1) · d,
despejando a1 en ambas expresiones e igualando resulta:
an = ak + (n – k).d
Interpolación de términos.
Supongamos que queremos intercalar entre 2 y 14 tres números a, b y c de manera que 2, a,
b, c, 14 estén en progresión aritmética.
GGG
105
Tenemos que a1 = 2, a5 = 14 y n = 5. Aplicando la expresión del término general de una
progresión aritmética, se tiene que:
a5 = a1 + 4d ; 14 = 2 + 4d : d = 3
Por tanto, la progresión aritmética es: 2, 5, 8, 11, 14.
Este problema, que consiste en intercalar varios términos entre dos dados, se denomina
interpolación. Los términos que hemos hallado se llaman medios aritméticos.
Suma de n términos consecutivos.
Consideremos la progresión formada por los seis primeros múltiplos de 5:
an : 5, 10, 15, 20, 25, 30.
Observemos que la suma de los extremos es:
a1 + a6 = 5 + 30 = 35
y que los términos equidistantes suman lo mismo que los términos extremos:
a2 + a5 = 10 + 25 = 35
a3 + a4 = 15 + 20 = 35
En general, en una progresión aritmética limitada se verifica:
a3 + an-2 = a2 + an-1 =... = a1 + an
En una progresión aritmética limitada, la suma de los términos equidistantes de los
extremos es igual a la suma de los extremos.
Vamos a utilizar este resultado para calcular la fórmula de la suma de n términos
consecutivos de una progresión aritmética. Veámoslo primero con el ejemplo:
¿Cuál es la suma de los seis términos de la progresión 5, 10, 15, 20, 25, 30?
Una forma de hallar la suma de los términos de esta progresión es escribir la suma dos
veces invirtiendo los términos en una de ellas.
GGG
106
S6 = 5 + 10 + 15 + 20 + 25 + 30
S6 = 30 + 25 + 20 + 15 + 10 + 5
2S6 = 35 + 35 + 35 + 35 + 35 + 35
2S6 = 6 · 35 = 6 · (5 + 30)
S6 = [6 · (5 + 30)]: 2 = 105
Vamos a generalizar este resultado: ¿Cuál es la suma de los términos de la progresión a1,
a2, a3,..., an-1, an?
Llamemos Sn a la suma de los n términos y escribamos la suma dos veces, invirtiendo los
sumandos en una de ellas.
Sn = a1 + a2 +... + an-1 + an
Sn = an + an-1 +... + a2 + a1
+
Sumando las dos igualdades resulta:
2Sn = (a1 + an) + (a2 + an-1) +... + (an-1 + a2) + (an + a1)
Como hay n paréntesis y el valor de cada uno es (a1 + an) se tiene:
2Sn = (a1 + an) + (a1 + an) +... + (a1 + an) = (a1 + an)·n
de donde:
GGG
107
Progresiones geométricas.
Observemos las potencias de 10 que resultan de la sucesión an = 10n-1.
1, 10, 102, 103, 104, 105,...
Cada término de esta sucesión es igual al anterior multiplicado por 10. Esta sucesión es una
progresión geométrica.
Una progresión geométrica es una sucesión de números tales que cada uno de ellos (salvo
el primero) es igual al anterior multiplicado por un número constante llamado razón, que se
representa por r.
Término general.
Según la definición anterior, en la progresión geométrica a1, a2, a3, a4, a5,..., an, se verifica:
a2 = a1 · r
a3 = a 2 · r = a1 · r · r = a1 · r 2
a 4 = a3 · r = a 1 · r 2 · r = a1 · r 3
Generalizando este proceso se obtiene el término general:
an = a1.r n - 1
Ejemplos:
•
•
¿Cuál es la razón de la progresión geométrica 3, 6, 12,...?
La razón se obtiene dividiendo un término por el anterior: r = 6 : 3 = 2.
¿Cuál es el quinto término de una progresión geométrica en la que a1 = 2 y r = 3?
Podemos ir hallando cada uno de los términos (2, 6, 18, 54, 162,...) multiplicando
cada término por 3. También se puede obtener directamente: a5 = a1 · r 5 - 1 = a1 · r 4;
a5 = 2 · 3 4 = 2 · 81 = 162
Se puede conseguir otra expresión para el término general en función de otro término
cualquiera, en lugar del primer término. Como an = a1 · r n - 1
y ak = a1 · r k - 1, despejando a1 en ambas expresiones e igualando resulta:
= ak · r n – k
an = ak.r n - k
GGG
108
Interpolación de términos.
Supongamos que queremos intercalar entre 3 y 96 cuatro números a, b, c y d de manera que
3, a, b, c, d, 14 estén en progresión geométrica.
Tenemos que a1 = 3, a6 = 96 y n = 6. Aplicando la expresión del término general de una
progresión geométrica, se tiene que:
a6 = a1 · r 5 ; 96 = 3 · r 5;
32 = r 5; r = 2
Por tanto, la progresión geométrica es: 3, 6, 12, 24, 48, 96.
Este problema, que consiste en intercalar varios términos entre dos dados, se denomina
interpolación. Los términos que hemos hallado se llaman medios geométricos o
proporcionales.
Producto de n términos consecutivos.
Observemos que en la progresión geométrica: 3, 6, 12, 24, 48
el producto de los términos extremos es:
3 · 48 = 144
y que el producto de los términos equidistantes de los extremos es también 144.
En general, en una progresión geométrica limitada se verifica:
a3 · an-2 = a2 · an-1 =... = a1 · an
En una progresión geométrica limitada, el producto de los términos equidistantes de los
extremos es igual al producto de los extremos.
Vamos a utilizar este resultado para calcular la fórmula del producto de n términos
consecutivos de una progresión geométrica. Llamemos Pn al producto de los n términos y
escribamos el producto dos veces, invirtiendo los factores en una de ellas.
Pn = a1 · a2 ·... · an-1 · an
Pn = an · an-1 ·... · a2 · a1
GGG
109
X
Multiplicando las dos igualdades resulta:
Pn2 = (a1 · an) · (a2 · an-1) ·... · (an-1 · a2) · (an · a1)
Como hay n paréntesis y el valor de cada uno es (a1 · an) se tiene:
Pn2 = (a1 · an) · (a1 · an) ·... · (a1 · an) = (a1 · an) n
de donde:
Suma de n términos consecutivos.
Si queremos calcular la suma de los términos de la progresión geométrica limitada a1, a2,
a3,..., an-1, an, escribimos la suma Sn de los n términos y después multiplicamos por la
razón.
Sn = a1 + a2 +... + an-1 + an
Sn· r = a1· r + a2· r +... + an-1· r + an· r
Ahora restamos Sn· r - Sn teniendo en cuenta que a1· r = a2, a2· r = a3, etc.
Sn· r - Sn = an· r - a1 : Sn· (r - 1) = an· r - a1,
de donde:
Usando la expresión del término general de una progresión geométrica an = a1· rn, se puede
obtener la fórmula de la suma en función de a1 y r así:
GGG
110
Suma de los términos de una progresión geométrica decreciente.
La progresión an = 2 · 10 1 - n: 2, 2/10, 2/100, 2/1000,... es una progresión geométrica de
razón positiva y menor que 1 (r = 1/10), es decir, es una progresión geométrica decreciente
e ilimitada y sus términos se hacen cada vez menores, pudiendo llegar a ser más pequeños
que cualquier número dado.
Para obtener la fórmula de la suma de estas progresiones multiplicamos por -1 el
numerador y el denominador de la fórmula anterior:
Si r es positivo y menor que la unidad, por ejemplo r = 1/100, ¿qué ocurre con la suma
anterior al crecer n?
La primera fracción permanece constante, pues no depende de n, pero rn se hace tan
pequeño como queramos. Por esta razón, para hallar la suma de los infinitos términos de
una progresión geométrica decreciente se utiliza esta fórmula:
GGG
111
Problemas propuestos con respuestas.
1) En una PA el 5to término es 11/3, el 7mo es 7. Si tiene 13 términos calcular: a) el
primero; b) el último c) la suma de los trece. Rta: a) -3 b) 17 c) 91
2) En una PG el 8vo término es ¼ y el 9no 0,125. Si tiene 20 términos calcular: a) el
primero; b) el último c) la suma de los veinte. Rta: a) 32 b) 1/214 c) 26 - 2-14
3) Un joven ahorra cada mes $5 más que el mes anterior. En 5 años sus ahorros sumarán $
9330.
Determinar
a) lo que ahorró el primer mes.
b) lo que ahorró el último mes.
Rta: a) $8 b) $303
4) Un padre proyecta colocar en un baúl $ 1 el día que su hijo cumpla un año, e ir
duplicando la cantidad sucesivamente en todos los cumpleaños. ¿Cuánto tendrá que colocar
el día que su hijo cumpla 18 años? ¿Cuánto habrá en el baúl luego? Rta: a) $131072 b)
$262143
5) Una máquina costó $ 9000. Se calcula que al final de cada año sufre una depreciación
igual al 15 % del valor que tiene al principio de ese año. ¿Cuál será su valor al cabo de 5
años? Rta: $3993,35
6) El número de bacterias de un cultivo está aumentando un 25 % cada hora. Si al principio
había 300000 ¿Cuántas bacterias habrá al cabo de 5 horas? Rta: 915527,34
7) El valor de un auto se deprecia 18 % cada año. Su precio original fue $ 19000. ¿Cuánto
valdrá al cabo de 9 años? Rta: $3184,77
8) Una ciudad tiene 600000 habitantes. La tasa de crecimiento de esa población es 8 %
anual. ¿Cuántos habitantes tendrá dentro de tres años? Rta: 755827,2
9) El valor de una mercadería se deprecia 4 % cada año. Su precio original fue de $ 19000.
¿Cuánto valdrá al cabo de 4 años? Rta $16137,58
10) La población de una ciudad aumenta en 35 % cada 10 años. Si su población en 1940 era
de 40000 habitantes, ¿cuál será su población en el año 2000? Rta: 242137,8
GGG
Siendo an una progresión aritmética, hallar:
112
11) El 9º término de an: 7, 10,13….
13) El 25º término de an:
12) El 12º término de an: 19, 12,5…
3 11
,
8 24
14) El 15º término de una progresión aritmética (PA) es 20 y la diferencia
15) Si a8 =
3
y a9 = 1 en una PA hallar a1
34
16) Si a92 = 1050 y a1 = -42 en una PA, hallar la diferencia.
Si se trata de una PA hallar la suma de:
17) Los 8 primeros términos de an: 15, 19,23….
18) Los 19 primeros términos de an:
3 3
, ….
4 2
5
19) Los 12 primeros términos de an: -5, -4 ,….
8
Interpolar en una PA:
20) 4 términos entre 5 y 12
21) 5 términos entre
3
1
y
4
8
22) 8 términos entre
1
7
y −
2
10
Hallar la suma de (PA)
23) 20 primeros múltiplos de 7
24) 100 primeros números impares mayores que 7
GGG
Progresiones Geométricas
113
2
. Hallar a1.
7
25) Hallar el 7º término de an: 3,6…..
12……
27) Hallar el 8º término de an:
26) Hallar el 8º término de an: -3,6,-
3
1 1
, − , ….
4
2 3
Resolver:
28) La razón de una PG es
29) a9 es
1
1
y a7 es
. Hallar a1
2
164
64
2
y r = . Hallar a1
2187
3
30) Hallar r de an:
729
3
,...., si n = 6
2
2
PG. Interpolar
31) 6 números entre 2 y 34
32) 7 números entre 8 y
11
64
1
32
PG: Hallar la suma
33) 5 primeros términos de an: 6, 3,
34) 10 primeros términos de an:
3
,……
2
1 1
, ,.....
4 2
Hallar, aplicando la fórmula de la suma de términos de PG, el valor de las siguientes
fracciones decimales:
35) 0,555….
36) 0,18111…..
37) 0.31818….
GGG
114
38) 2,1818….
ESTADÍSTICA
Es una ciencia que con base en la observación de hechos, en la recopilación de datos y en el
análisis de los mismos nos permite predecir situaciones futuras y proceder en consecuencia.
Por ejemplo, podemos hacer una encuesta sobre las preferencias electorales de los
colombianos para la presidencia y podemos predecir con muy poco margen de error quién
va a ser el presidente de Colombia, suponiendo que se haga una encuesta seria.
TÉRMINOS:
Datos: Es la información que se recoge y que luego se procesa.
Muestreo: Es el conjunto de técnicas que orientan la recolección de información.
Población o Universo: Es un conjunto, generalmente con un gran número de elementos del
cual se saca la información.
Muestra: Es un subconjunto de la población del cual tomamos la información
directamente. Esta muestra debe ser confiable en cuanto obtengamos una información veraz
y muy cerca de la realidad. Para esto también debe ser tomada al azar.
Ejemplo:
Se aplicó una prueba de Matemáticas a 30 estudiantes de 9º grado del Instituto Técnico
Central quienes obtuvieron los siguientes puntajes entre 10 y 50.
Tabla de datos:
10
45
35
50
30
25
30
45
20
40
35
25
50
40
35
25
35
30
Germán Giraldo Giraldo
115
20
45
30
25
25
40
15
35
30
35
45
35
Los datos son los puntajes que obtuvieron los estudiantes.
Muestreo: El tipo de examen.
Población o Universo: Los estudiantes del Instituto Técnico Central.
Muestra: Los 30 estudiantes de 8º grado a quienes se les aplicó la prueba.
Elaboremos una tabla de frecuencias para ver en qué consisten éstas.
TABLA DE FRECUENCIAS.
PUNTAJE FRECUENCIA
ABSOLUTA
10
1
15
1
20
2
25
5
30
5
35
7
40
3
45
4
50
2
SUMAS:
30
FRECUENCIA RELATIVA
FRACCIÓN DECIMAL PORCENTAJE
0,0333
3,33
1
30
0,0333
3,33
1
30
0,0666
6,66
2
30
0,1666
16,66
5
30
0,1666
16,66
5
30
0,2333
23,33
7
30
0,1
10
3
30
0,1333
13,33
4
30
0,0666
6,66
2
30
1,0000
100
30
30
Germán Giraldo Giraldo
OTROS TÉRMINOS: Con base en la tabla anterior podemos definir:
116
Frecuencia absoluta: Es el número de veces que aparece un dato. Por ejemplo, la
frecuencia absoluta del dato 40 es 3, porque aparece 3 veces en la tabla de datos.
Frecuencia relativa: E la relación (cociente) entre la frecuencia absoluta de un dato y el
5
ó 0,1666 ó 16,66%.
número de la muestra. La frecuencia relativa del dato 30 es
30
Moda: Es el dato de mayor frecuencia absoluta. En el ejemplo es 35 que tiene una
frecuencia absoluta de 7.
Media aritmética o Promedio: Es la suma de todos los datos de la muestra dividida por el
número de la muestra.
En el ejemplo la media aritmética o promedio es:
(10 + 15 + 20 + 20 + 25 +25 +25+ 25+ 25 + 30 + 30 + 30 + 30 + 30 + 35 + 35 + 35 + 35 +
35 + 35 + 35 + 40 + 40 + 40 + 45 + 45 + 45 + 45 + 50 + 50) ÷ 30=32,8
Mediana: La mediana se obtiene ordenando todos los datos en forma ascendente. El dato
que se encuentre en toda la mitad de la lista se llama mediana; esto, si el número de datos es
impar. Pero si el número de datos es par se promedian los dos que estén en la mitad,
obteniéndose así la mediana.
En el ejemplo:
10 – 15 – 20 -20 – 25 - 25 – 25 – 25 – 25 – 30 – 30 – 30 – 30 – 30 – 35 – 35 – 35 – 35 – 35
– 35 – 35 – 40 – 40 – 40 – 45 – 45 – 45 -45 – 50 - 50.
Los dos números centrales so 35 y 35. (35 + 35) ÷ 2 = 35. Ésta es la mediana.
La moda, la media aritmética y la mediana se llaman las Medidas de tendencia
Central.
Germán Giraldo Giraldo
117
Diagrama de líneas
7
6
Frecuencia
Absoluta
5
4
3
2
1
10
15 20
25
Datos (notas)
30
35
40
45
50
15 20
25
Datos (Notas)
30
35
40
45
50
Diagrama de Barras
7
6
Frecuencia
Absoluta
5
4
3
2
1
10
Germán Giraldo Giraldo
118
Diagrama circular:
Dividimos un círculo proporcionalmente a la frecuencia absoluta de cada dato, así:
360º ÷ 30 = 12º (30 es el número de la muestra; 360º es el número de grados de un
círculo). Este 12º es una constante que se va a multiplicar por la frecuencia de cada uno de
los datos, obteniendo así la parte de círculo (torta) que corresponde a cada dato según el
tamaño de su frecuencia absoluta.
12º x 1 = 12º (Parte del dato 10)
12º x 1 = 12º (Parte del dato 15)
12º x 2 = 24º (Parte del dato 20)
12º x 5 = 60º (Parte del dato 25)
12º x 5 = 60º (Parte del dato 30)
12º x 7 = 84º (Parte del dato 35)
12º x 3 = 36º (Parte del dato 40)
12º x 4 = 48º (Parte del dato 45)
12º x 2 = 24º (Parte del dato 50)
24º
12º
10
50
48º
12º
15
24º
20
45
25
.
40
36º
35
30
60º
84º
Germán Giraldo Giraldo
119
60º
Medidas de dispersión
Puntajes obtenidos por dos grupos de estudiantes sobre 100 puntos posibles.
GRUPO A
Puntaje
78
79
80
81
82
Frecuencia
1
2
3
2
1
GRUPO B
Puntaje
10
20
80
90
100
Frecuencia
1
1
4
3
1
Observamos que las medidas de tendencia central: media, mediana y moda son iguales en
el grupo A y los puntajes del grupo B están más dispersos.
Las medidas de dispersión son:
1) Recorrido
2) Desviación
3) Desviación media
4) Varianza
5) Desviación típica
Germán Giraldo Giraldo
120
A) Recorrido
Recorrido grupo A: El mayor puntaje menos el menor 82 – 78 = 4
Recorrido grupo B: El recorrido nos da una medida del grado de dispersión.
B) Desviación
Las desviaciones de un dato x respecto a la media es x – X
GRUPO A
Media 80
Puntaje
78
79
80
81
82
Desviación
78 – 80 = -2
79 – 80 = -1
80 – 80 = 0
81 – 80 = 1
82 – 80 = 2
GRUPO B
Media 72
Puntaje
10
20
80
90
100
Desviación
10 - 72 = - 62
20 – 72 = - 52
80 – 72= 8
90 – 72 = 18
100 – 72 = 28
C) La desviación media
Es el promedio de los valores absolutos de todas las desviaciones y se calcula de acuerdo
con la siguiente fórmula:
d =
d1
+
d 2 + d3 + ...... + d n
n
Germán Giraldo Giraldo
121
La desviación media de los puntajes del grupo A es:
d =
− 2 + − 1 × 2 + 0 × 3 + 1 ×2 +
2
9
La desviación media de los puntajes del grupo B es:
d =
−62 + − 52
= 0.88
+ 8 ×4 + 18 × 3 + 28
= 22.8
10
La aplicación de la fórmula y el sentido común nos indica que la desviación media de los
puntajes del grupo B es mayor que la desviación media de los puntajes del grupo A.
Ejercicio: Hallar la desviación media de las estaturas en centímetros de 7 estudiantes de
séptimo: 145; 150; 150; 160; 175; 150; 175.
D) La varianza
Hallamos cada desviación: x1 − X , x2 − X ,……. xn − X ,
Elevamos al cuadrado cada una de las desviaciones y sumamos los resultados:
(x
−X
1
)
2
+
(x
2
− X ) + ...... + ( xn − X )
2
2
Luego hallamos la media aritmética de dicha expresión:
(x
1
− X ) + ( x2 − X ) + ..... + ( xn − X )
2
2
2
n
Ese resultado se llama varianza.
La varianza de una serie de datos es la media de los cuadrados de las desviaciones.
Germán Giraldo Giraldo
122
E) Desviación típica
Es la raíz cuadrada positiva de la varianza.
σ =
(x
1
− X ) + ( x2 − X ) + ..... + ( xn − X )
2
2
2
n
Ejercicio:
1) Hallar el recorrido, la desviación media, la varianza y la desviación típica de los
siguientes datos:
75, 77, 76, 77, 77, 79, 78, 77
2) Las siguientes son las notas sobre 50 obtenidas por un grupo de alumnos de9º grado del
Instituto Técnico Central:
30, 50, 45, 50, 15, 40, 45, 40, 40, 30, 40, 50, 40, 45, 50, 40, 45, 50, 50, 25, 50, 50, 15, 20,
10.
Con respecto a estos datos:
a) Identificar: universo o población, muestra, moda, frecuencia absoluta de 45, frecuencia
relativa de 50.
b) Calcular: media aritmética y mediana.
c) Elaborar: diagramas de barras y circular.
d) Hallar el recorrido, la desviación media, la varianza y la desviación típica.
Germán Giraldo Giraldo
123
Tabla acumulada de frecuencias de datos agrupados.
Recurramos a la tabla de datos de las notas obtenidas por 30 estudiantes de 9º grado del
Instituto Técnico Central en una prueba de Matemáticas:
Tabla de datos:
10
45
35
50
30
25
30
45
20
40
35
25
50
40
35
25
35
30
20
45
30
25
25
40
15
35
30
35
45
35
Tabla de frecuencia acumulada
Clase
Intervalo
Marca
de clase
1
2
3
4
5
6
7
8
[10,15)
[15,20)
[20,25)
[25,30)
[30,35)
[35,40)
[40,45)
[45,50]
12,5
17,5
22,5
27,5
32,5
37,5
42,5
47,5
Frecuencia
absoluta
Frecuencia
relativa
1
1
2
5
5
7
3
6
3.3
3.3
6.7
16.7
16.7
23.3
10
20
Germán Giraldo Giraldo
124
Frecuencia relativa
acumulada
Absoluta Porcentual
1
3.3
2
6.6
4
13.3
9
30
14
46.7
21
70
24
80
30
100
´Gráfico de frecuencia acumulada
100%
95%
90%
85%
80%
Q3
75%
70%
65%
60%
46.7%
Q2
55%
50%
45%
40%
35%
30%
Q1
13.3%
25%
20%
15%
10%
6.6%
3.3%
10
15
20
25
30
28.5
Germán Giraldo Giraldo
125
35
35.7
40
45
42.5
50
En la tabla de frecuencia acumulada dividimos los datos en 8 intervalos y los llamamos
clases. Todos los intervalos, excepto el último son cerrados al principio y abierto al final.
Hay una columna para la marca de clase que es el promedio de los extremos de cada
intervalo.
Hay otra columna para la frecuencia absoluta de cada intervalo.
Otra para la frecuencia relativa de cada intervalo.
La última dividida en dos para la frecuencia absoluta acumulada y la frecuencia relativa
acumulada.
En el gráfico de frecuencia relativa acumulada tenemos en el eje de las x los intervalos y en
el eje de las y los porcentajes o frecuencia relativa.
El área que corresponde en el gráfico a cada intervalo va determinada por barras que cada
vez van acumulando el área de los anteriores intervalos.
Concepto de Cuartil: Cuando la distribución de frecuencias se subdivide en cuatro partes
iguales, a cada uno de los valores que marcan esas partes se les denomina cuartiles y se
simbolizan así: Q1 , Q2 , Q 3. El primer cuartil, Q1, es un número tal que, a lo sumo, el 25%
de los datos es menor que él, y, a lo sumo, el 75% de los datos es mayor que él.
El segundo cuartil, Q2, es la mediana.
El tercer cuartil, Q3, es un número tal que, a lo sumo, el 75% de los datos es menor que él,
y, a lo sumo, el 25% de los datos es mayor que él.
Dividimos el gráfico en 4 cuartiles:
Q1 (Primer cuartil) está limitado en el gráfico por los ejes del plano cartesiano y dos
segmentos que se cortan en el punto del plano cartesiano con coordenadas (28.5;25%).
El 28.5 lo calcularemos luego y lo muestra aproximadamente el gráfico.
28.5 puntos significa que el 25% de los estudiantes obtuvieron puntajes inferiores a 28.5.
Q2 (Segundo cuartil): está limitado en el gráfico por los ejes del plano cartesiano y dos
segmentos que se cortan en el punto del plano cartesiano con coordenadas (35.7; 50%).
El 35.7 lo calcularemos luego, pero el gráfico lo muestra aproximadamente.
35.7% significa que los estudiantes que tengan puntajes inferiores son superados por el
50% de los alumnos.
Germán Giraldo Giraldo
126
Q3 (Tercer cuartil): Está limitado en el gráfico por los ejes de coordenadas y dos segmentos
que se cortan en el punto del plano cartesiano con coordenadas (42.5;25%).
42.5 significa que los estudiantes que tengan puntajes superiores, están entre el 25% de los
mejores.
Cuartiles
Q1 (Primer cuartil):
Número de estudiantes
30
=
= 7.5 estudiantes.
4
4
Q2 (Segundo cuartil): 7.5 x 2 = 15 estudiantes.
Q3 (Tercer cuartil): 7.5 x 3 = 22.5 estudiantes.
Proceso matemático:
Número de estudiantes
30
=
= 7.5 estudiantes.
4
4
Este número está en la clase 4 cuyo acumulado llega a 9; el anterior acumulado es 4.
7.5
– 4 = 3.5
Para saber cuánto más de 25, que es el primer elemento de clase 4, se necesita trabajamos
con una regla de tres:
Puntaje del intervalo
Nº de estudiantes del intervalo
5
5
x
3.5
Para cuartil 1
x =
5 × 3.5
= 3.5
5
Q1 = 25 + 3.5 = 28.5 (Puntaje)
Para cuartil 2
Número de estudiantes
30
=
× 2 = 15 estudiantes.
4
4
Este número está en la clase 6 cuyo acumulado llega a 21; el anterior acumulado es 14.
15 – 14 = 1
Germán Giraldo Giraldo
127
Para saber cuánto más de 35, que es el primer elemento de clase 6, se necesita trabajamos
con una regla de tres:
Puntaje del intervalo
Nº de estudiantes del intervalo
5
7
x
1
x =
5 ×1
= 0.7
7
Q2 = 35 + 0.7 = 35.7 (Puntaje)
Para cuartil 3 Nº de estudiantes = (7.5)(3) = 22.5 estudiantes
Este número está en la clase 7 cuyo acumulado llega a 24; el anterior acumulado es 21.
22.5 - 21 = 1.5
Para saber cuánto más de 40, que es el primer elemento de clase 7, se necesita trabajamos
con una regla de tres:
Puntaje del intervalo
5
x
x =
Nº de estudiantes del intervalo
3
1.5
5 × 1.5
= 2.5
3
Q3 = 40 + 2.5 = 42.5 (Puntaje)
Germán Giraldo Giraldo
128
PROBABILIDAD
La probabilidad mide la mayor o menor posibilidad de que se dé un determinado resultado
(suceso) cuando se realiza un experimento aleatorio.
La probabilidad toma valores entre 0 y 1 (o expresados en tanto por ciento, entre 0% y
100%):
El valor cero corresponde al suceso imposible: lanzamos un dado al aire y la
probabilidad de que salga el número 7 es cero (al menos, si es un dado certificado por la
OMD, "Organización Mundial de Dados").
El valor uno corresponde al suceso seguro: lanzamos un dado al aire y la probabilidad de
que salga cualquier número del 1 al 6 es igual a uno (100%).
El resto de sucesos tendrá probabilidades entre cero y uno: que será tanto mayor cuanto
más probable sea que dicho suceso tenga lugar.
¿Cómo se mide la probabilidad?
Uno de los métodos más utilizados es aplicando la Regla de Laplace: define la
probabilidad de un suceso como el cociente entre casos favorables y casos posibles.
P(A) = Casos favorables / casos posibles
Veamos algunos ejemplos:
a) Probabilidad de que al lanzar un dado salga el número 2: el caso favorable es tan
sólo uno (que salga el dos), mientras que los casos posibles son seis (puede salir cualquier
número del uno al seis). Por lo tanto:P(A) = 1 / 6 = 0,166 (o lo que es lo mismo, 16,6%)
b) Probabilidad de que al lanzar un dado salga un número par: en este caso los casos
favorables son tres (que salga el dos, el cuatro o el seis), mientras que los casos posibles
siguen siendo seis. Por lo tanto:
P(A) = 3 / 6 = 0,50 (o lo que es lo mismo, 50%)c) Probabilidad de que al lanzar un dado
salga un número menor que 5: en este caso tenemos cuatro casos favorables (que salga el
uno, el dos, el tres o el cuatro), frente a los seis casos posibles. Por lo tanto: P(A) = 4 / 6 =
0,666 (o lo que es lo mismo, 66,6%) GGG
d) Probabilidad de que nos toque el "Gordo" de Navidad: tan sólo un caso favorable, el
número que jugamos (¡qué triste...¡), frente a 100.000 casos posibles. Por lo tanto:
P(A) = 1 / 100.000 = 0,00001 (o lo que es lo mismo, 0,001%)
129
Merece la pena...... Por cierto, tiene la misma probabilidad el número 45.264, que el
número 00001, pero ¿cuál de los dos comprarías?
Para poder aplicar la Regla de Laplace el experimento aleatorio tiene que cumplir dos
requisitos:
a) El número de resultados posibles (sucesos) tiene que ser finito. Si hubiera infinitos
resultados, al aplicar la regla "casos favorables / casos posibles" el cociente siempre sería
cero.
b) Todos los sucesos tienen que tener la misma probabilidad. Si al lanzar un dado,
algunas caras tuvieran mayor probabilidad de salir que otras, no podríamos aplicar esta
regla.
A la regla de Laplace también se le denomina "probabilidad a priori", ya que para
aplicarla hay que conocer antes de realizar el experimento cuales son los posibles
resultados y saber que todos tienen las mismas probabilidades.
¿Y si el experimento aleatorio no cumple los dos requisitos indicados, qué hacemos?,
¿ponemos una denuncia?
No, no va a ser necesario denunciar a nadie, ya que en este caso podemos acudir a otro
modelo de cálculo de probabilidades que se basa en la experiencia (modelo frecuentista):
Cuando se realiza un experimento aleatorio un número muy elevado de veces, las
probabilidades de los diversos posibles sucesos empiezan a converger hacia valores
determinados, que son sus respectivas probabilidades.
Ejemplo: si lanzo una vez una moneda al aire y sale "cara", quiere decir que el suceso
"cara" ha aparecido el 100% de las veces y el suceso "cruz" el 0%.
Si lanzo diez veces la moneda al aire, es posible que el suceso "cara" salga 7 veces y el
suceso "cruz" las 3 restantes. En este caso, la probabilidad del suceso "cara" ya no sería del
100%, sino que se habría reducido al 70%.
GGG
Si repito este experimento un número elevado de veces, lo normal es que las probabilidades
de los sucesos "cara" y "cruz" se vayan aproximando al 50% cada una. Este 50% será la
probabilidad de estos sucesos según el modelo frecuentista.
En este modelo ya no será necesario que el número de soluciones sea finito, ni que todos
los sucesos tengan la misma probabilidad.
130
Ejemplo: si la moneda que utilizamos en el ejemplo anterior fuera defectuosa (o estuviera
trucada), es posible que al repetir dicho experimento un número elevado de veces, la "cara"
saliera con una frecuencia, por ejemplo, del 65% y la "cruz" del 35%. Estos valores serían
las probabilidades de estos dos sucesos según el modelo frecuentista.
A esta definición de la probabilidad se le denomina probabilidad a posteriori, ya que tan
sólo repitiendo un experimento un número elevado de veces podremos saber cual es la
probabilidad de cada suceso.
Ejercicios:
Ejemplo: Hay 9 balotas numeradas en una urna. Seis balotas tienen números impares. La
6
2
= .
probabilidad de sacar un número impar es:
9
3
1) Ahora hay balotas con los números 12, 2, 10, 9, 11, 6, 8 ,3, 1, 7, 4, 5.
¿Cuáles son las oportunidades de coger una balota con un número de los siguientes?
a) Impar b) Un 2 o un 1. c) Menor que 7. d) Mayor que 8. e) Par. f) Mayor que 7 y
menor que 5. g) Mayor o igual que 3 y menor o igual que 9.
2) Si hay 15 balotas numeradas del 1 al 15 qué oportunidades hay de sacar un número de
los siguientes?
a) Par b) Que sea 3 ó 4.
c) Mayor que 5.
d) Menor que 4.
e) Mayor o igual que
3 y menor o igual que 7
e) Mayor o igual que 3 ó menor o igual que 7.
f) Impar
g) Mayor que 1
h) Menor que 5.
GGG
131
En la probabilidad se estudian situaciones en donde se pueden esperar varios resultados y
no solamente uno.
Ejemplo 1:
Pablo está preocupado porque olvidó hacer su tarea y no sabe si asistir o faltar a clase,
porque así como es “probable” que el profesor le pregunte, también es “probable” que esto
no suceda.
Pablo tiene dos posibilidades:
A: Asistir a clase.
B: No asistir a clase.
A cada una de estas dos situaciones las llamaremos eventos. Dado que los dos eventos no
se pueden dar al mismo tiempo porque es imposible que Pablo simultáneamente entre a
clase y no asista, entonces se dice que son eventos independientes.
¿Cuál es la probabilidad de que Pablo asista a clase? Como únicamente puede darse una de
las dos situaciones, diremos que:
Probabilidad de que Pablo asista:
1
2
Es decir, la probabilidad es una razón entre el número de resultados posibles y el número
total de eventos.
También se puede decir que hay 50% de probabilidad de que asista a clase y 50% de que
no lo haga.
Ejemplo 2.
En un cuadrangular de fútbol donde todos los equipos están igualmente preparados, ¿cuál
es la probabilidad de cada uno de obtener el título?
Como están participando 4 equipos hay cuatro eventos, y como no pueden ganar todos al
tiempo, los eventos son independientes. Por tanto:
Probabilidad de ser el equipo campeón: P =
Un _ campeón
1
= = 0,25
Cuatro _ Participantes 4
GGG
Expresado en porcentaje, cada equipo tiene el 25% de probabilidad de ser el campeón del
cuadrangular.
132
Definiciones
La probabilidad es la posibilidad numérica de que ocurra un evento y se mide utilizando
valores comprendidos entre 0 y 1.
Un experimento es toda acción bien definida que nos lleva a un resultado único.
Un experimento aleatorio es un proceso o acción en el cual se pueden esperar varios
resultados.
El espacio muestral de un experimento aleatorio, notado como S, es el conjunto de todos
los posibles resultados que se pueden obtener al realizar el experimento.
Un evento es un subconjunto de todos los resultados posibles y se representa por E.
La probabilidad de ocurrencia de un evento se define como el número de veces que puede
ocurrir dicho evento dividido entre el total de posibles resultados. Es decir, la probabilidad
de que suceda un evento E está dada por
P(E) =
Cantidad _ de _ elementos _ de _ E
Cantidad _ de _ elementos _ de _ S
Ejemplo 3.
¿Cuál es la probabilidad de que un ser humano muera?
Hasta ahora no se ha conocido el caso de un ser humano que tenga cuerpo inmortal; por lo
tanto, la probabilidad que tenemos de morir es 1 o del 100%.
Ejemplo 4
¿Cuál es la probabilidad que al ordeñar una vaca la leche que se obtenga sea negra?
Nunca hemos sabido de una vaca que produzca leche negra. Como este evento es
imposible, la probabilidad de que suceda es cero. GGG
Ejemplo 5
¿Cuál es la probabilidad de obtener un 5 al lanzar un dado una sola vez?
133
Sabemos que el dado tiene 6 caras numeradas así: 1, 2, 3, 4, 5, 6; por lo tanto la
1
probabilidad de sacar un 5 es de .
6
De los ejemplos anteriores podemos establecer una escala de posibilidades tomando los
valores comprendidos entre cero y uno.
CONCEPTO DE EVENTO
Llamaremos evento a cada caso posible, o sea la realización de un acontecimiento. Un
evento puede ser:
Cierto: cuando existe la certeza absoluta. P = 1
Verosímil: cuando 0,5 ⟨ P ⟨1
Dudoso: cuando P = 0,5
Inverosímil: cuando 0 ⟨ P ⟨0,5
Imposible: cuando P = 0
PROBABILIDAD CONDICIONAL
Ejemplo 6
Supongamos que está visitando una pareja de la que sabe que tiene dos hijos. Durante la
visita entra uno de los hijos, un niño. Señale qué probabilidad hay de que el otro hijo sea
también niño, si:
a. No sabe cuál de los dos es mayor.
b. Sabe que el hijo que entró es el mayor de los dos.
Solución.
a. La probabilidad de ocurrencia de un evento se define como la división entre el
número de elementos del evento y el número de elementos del espacio. Si o indica
la posibilidad de ser niño y a la posibilidad de ser niña, entonces el conjunto que
contiene todas las posibilidades del espacio muestral, será S = (oo, oa, ao, aa); estas
son las cuatro posibilidades de tener dos hijos, donde la primera letra representa al
hijo mayor y la segunda al hijo menor. A = (oo, oa, ao) es el evento que haya por lo
3
menos un niño entre los dos hijos. Luego la probabilidad es P(A) =
4
b. Llamemos B al evento de tener dos hijos y que el mayor sea niño; entonces:
2
B = (oo, oa). La probabilidad P(A/B) =
4
PROBABILIDAD CONDICIONAL es la probabilidad de que el evento A ocurra, dado
134
que el evento B ya ocurrió.
La forma de calcularlo consiste en dividir la cantidad de elementos del evento A ∩ B entre
los elementos del evento B: P(A/B) = P(A ∩ B) / P( B)
Ejemplo 7.
Supongamos que en un pueblo la población total que ha reunido los requisitos para
graduarse está clasificada en la siguiente tabla:
Hombre
Mujer
Total
Empleados
460
140
600
Desempleados
40
260
300
Total
500
400
900
Si se selecciona al azar a uno de los individuos para que realice un programa de televisión,
responda:
a. Si el elegido es una persona empleada, ¿cuál es la probabilidad de que además sea hombre?
b.Si el elegido es un hombre, ¿cuál es la probabilidad que además sea empleado?
Llamemos H al evento que se produce al escoger un hombre y E al evento que se produce
al escoger un empleado.
a.
La P(H/E) = (H ∩ E ) / E =
= (número de personas que son hombres y empleados)/ (número de empleados)
P(H/E) = 460/500 = 23/30
GGG
b. P(E/H) = (H ∩ E ) / H = 460 / 500 = 23 / 25
Ejemplo 8
Al lanzar un dado seis veces, ¿es cierto que en cada ocasión se obtiene un número
diferente?
No, pues cada vez que los dados se lanzan, todas las caras tienen la misma probabilidad de
salir.
Ejemplo 9
Un corredor de bolsa sabe por experiencia que la probabilidad de que un cliente compre
acciones es del 65%. La probabilidad de que el cliente compre un bono del gobierno, si ya
tiene acciones, es del 35%. ¿Son los dos eventos independientes?
135
Si B es el evento de que el cliente compre acciones y S la probabilidad de que compre un
bono del gobierno, entonces: P( ∩ B) = P ( S / B ) XP( B ) = 0,35 X 0,65 = 0,22
En conclusión: NO son eventos independientes, porque la probabilidad P(S/B) no es igual a
P(S)
Independencia
Un evento B es independiente de otro evento A si la probabilidad de ocurrencia de B no
está afectada por la ocurrencia o no de A. Es decir, dos eventos son independientes si el
resultado de uno no afecta el resultado del otro
Esto significa que: P(B) = P(B/A)
1.La siguiente tabla muestra la clasificación de 150 estudiantes de grado once de un colegio
de Bogotá, de acuerdo con el género y la especialización que han escogido para cursar su
media vocacional.
Especializaciones
Hombre
Mujer
Totales
25
20
45
20
37
57
46
2
48
91
59
150
a. Si se selecciona un estudiante al azar y resulta ser hombre, ¿ cuál es la probabilidad
de que su especialización sea en artes?
b. Si se selecciona un estudiante al azar y su especialización es el tecnología, ¿Cuál es
la probabilidad de que sea mujer?
TÉCNICAS DE CONTEO
En este tema se presentarán algunas técnicas que permiten determinar el número de
elementos del espacio muestral de acuerdo con las características del experimento. Estas
técnicas son llamadas técnicas de conteo o técnicas de enumeración.
Llamamos técnicas de conteo las formas de determinar el número de elementos de un
conjunto.
Los elementos a contar son los resultados posibles, a partir de un experimento aleatorio, es
decir, las formas de conteo nos permiten calcular el número de elementos de un espacio
muestral.
Entre las formas de conteo tenemos:
-Las permutaciones.
-Las variaciones.
-Las combinaciones
136
PERMUTACIONES
Los elementos de un conjunto se pueden organizar de diferentes formas y a esta variedad
de combinaciones se les llama permutaciones. Podemos hacer permutaciones sin
sustitución y permutaciones con sustitución.
Ejemplo 1
Si tenemos tres pedazos de tela del mismo tamaño y de diferentes colores (amarillo, verde,
rojo), ¿Cuántas banderas con los colores ubicados uno encima del otro se pueden armar?
Sea a = amarillo; v = verde; r = rojo. Podemos formar las siguientes banderas: avr, arv, var,
vra, rav y rva. Es decir, en total se pueden formar 6 banderas.
El número total de banderas sería entonces: 3 X 2 X 1 = 3!
Ejemplo 2.
Considere ahora cuatro colores representados por las letras m, z, r y v. ¿Cuántos tipos de
banderas diferentes de cuatro colores se pueden hacer?
La primera letra puede ser: m, z, r, v
La segunda en cada caso crea tres posibilidades: mz, mr, mv, zm, zr, zv, rm, rz, rv, vm, vz,
vr
La tercera letra, en cada caso, crea dos posibilidades más:
mzr, mzv, mrv, mrz, mvz, mvr, zmr, zmv, zrm, zrv, zvr, zvm, rmz, rmv, rzm, rzv, rvm, rvz,
vmz, vmr, vzr, vzm, vrm, vrz
El último color, en cada caso, al completar la bandera de cuatro colores:
mzrv, mzvr, mrvz, mrzv, mvzr, mvrz, zmrv, zmvr, zrmv, zrvm, zvrm, zvmr, rmzv, rmvz,
rzmv, rzvm, rvmz, rvzm, vmzr, vmrz, vzrm, vzmr, vrmz, vrzm
Con cuatro colores se puede armar de 24 formas la bandera, es decir, 4 X 3 X 2 X 1
Cuando contamos la cantidad de formas como se puede ordenar un conjunto de objetos,
donde cada objeto debe aparecer una sola vez, estamos contando las permutaciones sin
sustitución del conjunto.
&&&&&&&&
137
Cálculo de permutaciones sin sustitución
El número de permutaciones sin sustitución de un conjunto de n elementos se calcula de la
siguiente forma:
nPn = n x (n-1) x (n-2) x…x 3 x 2 x 1,
donde n representa la cantidad de elementos del conjunto que debe ser multiplicado por
todos los números naturales anteriores a él.
Ejemplo 3
Si no sabemos qué colores tenemos, pero solo hay dos opciones posibles, ¿cuántas banderas
podemos armar?
Solución: 2 x 1 = 2 banderas. Es decir, corresponde a una permutación sin sustitución.
GGG
Ejemplo 4
En una bolsa hay cuatro balotas de diferentes colores. Si se sacan de una en una y se
ordenan una a la derecha de la anterior, ¿cuántas permutaciones se pueden formar?
A pesar no saber los colores de las balotas, estamos buscando el número total de formas en
que se pueden ordenar, colocando una a la derecha del anterior; es decir, se trata de una
permutación sin sustitución. Luego:
Pn = n(n-1)(n-2)(n-3); entonces P4 = 4(3)(2)(1) = 24 formas
Ejemplo 5
Volvamos al ejemplo de las banderas. Si tenemos tres pedazos de tela del mismo tamaño y
de diferentes colores (amarillo, verde, rojo), ¿Cuántas banderas con los colores ubicados
uno encima del otro se pueden armar si se puede repetir una o más veces cada color?
Sea a = amarillo; v = verde; r = rojo.
El primer color se puede escoger de tres formas diferentes: a, v, r
Para cada una de las tres formas, el segundo color se puede escoger otra vez de tres formas
diferentes: aa, av, ar, va, vv, vr, ra, rv, rr
&&&&&&&&
138
A cada una de las nueve formas anteriores se le puede adicionar de tres formas diferentes
el tercer color: aaa, aav, aar, ava, avv, avr, ara, arv, arr, vaa, vav, var, vva, vvv, vvr, vra,
vrv, vrr, raa, rav, rar, rva, rvv, rvr, rra, rrv, rrr.
Es decir, completamos 27 formas de banderas igual a ( 3 )3 formas de banderas.
Cuando contamos la cantidad de formas como se puede ordenar un conjunto de objetos,
donde cada objeto puede aparecer más de una vez, estamos contando las permutaciones
con sustitución del conjunto.
Cálculo de permutaciones con sustitución
El número de permutaciones con sustitución de un conjunto de n elementos se calcula así:
Permutaciones con sustitución: n x n x n x n x … x n x n x n; n veces., es decir ( n )n
Ejemplo 6
¿Cuántos números hay entre 0 y 10 000 que contengan los dígitos 1, 2, 3, 4, por lo menos
una vez?
Decir que contengan los dígitos 1, 2, 3, 4, por lo menos una vez, significa que cada dígito
se puede repetir, como sucede, por ejemplo, con el número 3333. Por tanto corresponde a
una permutación con sustitución de 4 elementos: ( 4 )4 = 256
Ejemplo 7
En una bolsa hay 6 balotas marcadas con los números del 1 al 6. Si se sacan de una en una
las balotas para formar el número ganador de una lotería y en cada caso la balota escogida
se devuelve a la bolsa y tiene la posibilidad de volver a ser escogida, ¿cuántos números se
pueden formar?
A pesar de que estamos contando en este caso posibilidades y no formas de ordenar, porque
solamente tenemos 6 balotas, podemos aplicar el mismo método de conteo:
Permutaciones con sustitución de 6 elementos: ( 6 )6 = 46 656
139
Permutaciones r sin repetición
Ejemplo 8
Supongamos que usted dispone de 5 colores (amarillo, rojo, verde, lila, negro) para realizar
un trabajo, pero solo puede utilizar un color para la parte superior del trabajo y otro color
para la parte inferior del trabajo. ¿Cuántas posibilidades tiene de escoger 2 colores
diferentes?
Sea: a = amarillo; r = rojo; v = verde; l = lila; n = negro.
Para cada color, tiene 4 posibilidades para escoger el segundo, así:
ar; av; al; an;
ra; rv; rl; rn;
la; lr; lv; ln; va; vr; vl; vn;
na; nr; nv; nl;
En total, tendré 5 x 4 = 20 posibilidades de escoger dos colores
Esta posibilidad de escoger 2 colores de 20 se llama una permutación.
Concepto de permutación
Una ordenación de solamente r elementos de un total de n objetos disponibles se llama una
permutación r.
El número de permutaciones r objetos de un total de n sin repetición , se calcula como
n!
nPr =
; o P(n, r) = n x ( n-1) x ( n – 2) x …x (n – r + 1)
(n − r )!
La fórmula indica que se debe multiplicar el número de objetos en total por todos los
números anteriores, hasta un número superior a la cantidad de objetos que se toman.
&&&&&
Ejemplo 9
De cuántas formas se pueden organizar 7 libros formados en grupos de a 4?
Claramente es una permutación en la que no se toman todos los elementos, a ese tipo de
permutación también se le llama variación. Luego:
7!
7! 7 x6 x5 x 4 x3 x 2 x1
= =
= 7x6x5x4 = 840
7P4 =
(7 − 4)! 3!
3 x 2 x1
Es decir, los libros se pueden organizar de 840 formas diferentes
140
También lo hubiera podido calcular así: como n = 7 y r = 4, n – r + 1 = 7 – 4 + 1 = 4
P(7,4) = 7 x 6 x 5 x 4 = 840
Ejemplo 10
¿Cuántos “tríos” de letras se pueden formar con las letras de la palabra “murciélago”?
Observe que se tienen 10 letras distintas y se desean sacar solamente 3 de ellas:
P(10, 3) =
n!
10!
10!
=
=
= 10 x9 x8 = 720 tríos de letras
(n − r )! (10 − 3)! 7!
COMBINATORIAS
Ejemplo 11
Si tenemos 4 colores (amarillo, rojo, morado, verde) y debemos utilizar solo 3 para pintar
un círculo en forma de tajadas, ¿de cuántas maneras distintas podemos hacerlo?
Puedo combinar sin importar el orden así: arm, arv, rmv, vma. Para cada caso no importa el
orden, es decir: arm = amr = ram = rma = mar = mra;
De igual forma: arv = avr = rav = rva = var = vra
Lo mismo para: rmv = rvm = mrv = mvr = vrm = vmr
Finalmente:
vma = vam = mva = mav = avm = amv
Como no importa el orden de los colores, concluimos que hay cuatro soluciones para
escoger los tres colores.
Concepto de combinatoria:
Cuando seleccionamos de un grupo de n objetos solamente r de ellos sin tener en cuenta el
orden, lo llamamos una combinación de n objetos tomados r a la vez
El número de combinaciones de n objetos tomados de r en r se expresa como:
n!
C(n, r) = nr =
r!(n − r )!
4! 4 x3 x 2 x1
Para el ejemplo 11, se tiene: n = 4, r = 3, n – r = 4 – 3; luego C(4, 3) =
=
=4
1! x3! 1x3 x 2 x1
formas distintas.
()
GGG
141
Ejemplo 12
De los 12 estudiantes inscritos para el campeonato de baloncesto se deben escoger 5
titulares para comenzar la primera ronda. ¿De cuántas maneras se pueden seleccionar los
titulares?
Esta situación corresponde a una combinación porque se tienen 12 personas, de las cuales
se deben escoger solo 5. En este caso no se tiene en cuenta el orden en que se escojan,
porque lo importante es que se queden en la titular.
12!
= 792 formas.
Luego, como n = 12; r = 5; n – r = 7; C(12,5) =
(12 − 5)! x5!
EJERCICIOS PROPUESTOS
1. Una constructora desea lanzar una nueva etapa de sus casas para la venta. En esta nueva
etapa cada comprador tiene la ventaja de escoger el estilo de la fachada: rústico, colonial
y tradicional, lo mismo que el número de pisos: un piso, dos pisos, tres pisos o con
desniveles. ¿De cuántas formas puede un comprador ordenar su casa?
1.Se sacan tres billetes de a lotería entre 20 billetes posibles., para asignar el primero, el
segundo y el tercer premio. Encontrar el número posible de asignación de los premios.
2.Se desea formar algunos comités de profesores para la representación de los docentes
ante el Consejo Directivo. Para la elección de los Comités se tienen siete candidatos:
cuatro del área técnica y tres del área académica. Un comité consta de tres personas.
a. ¿Cuántos comités de tres personas se pueden conformar?
b.Si se quiere que en un comité halla dos técnicos y un académico, ¿de cuántas formas se
pueden conformar los comités?
Triángulo de Pascal
¿Recuerda la siguiente estructura numérica?
1
1
1
1
1
2
3
1
3
1
1 4 6 4 1
5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1
Es el Triángulo de Pascal, que sirve para hallar los coeficientes de los términos obtenidos al
desarrollar el Binomio de Newton.
Este triángulo nos sirve además para hallar el número de soluciones (combinaciones) que se
pueden lograr en un conjunto dado. Por ejemplo, si tomamos el quinto renglón del arreglo:
142
1. 4 6 4 1, lo podemos interpretar de la siguiente manera:
De un grupo de 4 personas se pueden formar:
a. Un equipo de 4 personas.
b. 4 equipos de 3 personas.
c. 6 equipos de 2 personas
d. 4 equipos de 1 persona.
e. 1 equipo de 0 personas.
Ejemplo 13
Empleando el Triángulo de Pascal y la fórmula para combinatoria, resolver el siguiente
problema: ¿Cuántos equipos de 3 personas se pueden formar de un grupo de 5 personas?
Tomamos del Triángulo de Pascal el renglón donde el segundo término sea 5:
1
5 10 10 5 1
Interpretamos ese renglón así: De un grupo de 5 personas se pueden formar:
a. Un equipo de 5 personas
b. 5 equipos de 4 personas.
c. 10 equipos de 3 personas.
d. 10 equipos de 2 personas.
e. 5 equipos de 1 persona.
f. 1 equipos de 0 personas.
Es decir, podemos formar de un grupo de 5 personas, 10 equipos de 3 personas.
Empleando la fórmula para combinatoria
5!
⎛5⎞
n = 5; r = 3; n – r = 2; luego ⎜ ⎟ =
= 10 ; resultado idéntico al obtenido en el
⎝ 3 ⎠ 3! x 2!
Triángulo de Pascal.
EJERCICIOS DE PROBABILIDAD
1. ¿Cuál es la probabilidad de obtener siete puntos en el lanzamiento de dos dados?
a) 1/6
b) 1/2
c) 7/12
143
d) 7/36
e) 7/2
2. Al lanzar dos monedas, qué probabilidad hay de obtener una cara y un sello?
a) 4
b) 2
c) 1
d) 1/2
e) 1/4
3. Una caja contiene 12 bolas negras y 8 rojas, ¿qué probabilidad hay de no sacar una bola
negra?
a) 2/5
b) 3/5
c) 2/3
d) 3/2
e) 8
4. Se lanza un dado y sale 4. ¿Qué probabilidad hay de que al lanzarlo nuevamente sume
con el primer resultado un número menor que 9?
a) 1/9
b) 5/6
c) 7/36
d) 4/9
e) 2/3
5. En un curso de 60 alumnos, 1/3 de los alumnos habla inglés, 1/4 habla francés y 1/10
habla los dos idiomas, ¿cuál es la probabilidad de que un alumno elegido al azar hable sólo
un idioma?
a) 1/3
b) 1/4
c) 23/60
d) 29/60
e) 7/12
6. ¿Cuál de las siguientes expresiones no corresponde a un suceso aleatorio?
a) Jugar un
juego de azar
b) Enfriar agua c) Lanzar una
a 0º C.
piedra y medir
su alcance
d) Preguntarle a e) Apostar en
un desconocido una carrera de
si fuma
caballos
7. ¿Qué probabilidad hay de que la lanzar 2 dados se obtenga una suma menor que 6?
a) 10
b) 5/6
c) 1/6
d) 5/18
e) 5/36
GGG
8. ¿Cuál es la probabilidad de ganar el premio de un rifa para la cual se venden 20 listas y
cada lista tiene 20 números, si se compran 4 números?
a) 1/100
b) 1/10
c) 1/5
d) 1/4
e) Ninguna de
las anteriores
9. ¿Cuántos elementos tiene el espacio muestral que se obtiene al lanzar 3 monedas?
a) 27
b) 9
c) 8
d) 6
e) 3
10. Al lanzar un dado 2 veces consecutivas, ¿qué probabilidad hay de obtener primero un 3
y luego un número par?
a) 1/3
b) 1/12
c) 1/9
144
d) 2/3
e) 4
11. En una bolsa se echan 12 bolitas numeradas correlativamente del 1 al 12. Calcular la
probabilidad de obtener un número menor que 5 o múltiplo de 5 al sacar una de ellas.
a) 1/2
b) 1/3
c) 1/6
d) 1/18
e) 0
12. Calcular la probabilidad de obtener dos ases de un naipe de 52 cartas, sin devolver la
primera carta al naipe.
a) 1/26
b) 1/352
c) 4/663
d) 1/221
e) 3/674
13. Al lanzar dos dados, ¿cuál es la probabilidad de obtener un puntaje menor que 5 ó
mayor que 10?
a) 1/72
b) 1/12
c) 1/4
d) 1/6
e) Ninguna de
las anteriores
14. Calcular la probabilidad de que al sacar dos fichas de una bolsa, que contiene 3 fichas
rojas y 4 blancas, con reposición, ambas sean fichas rojas.
a) 3/4
b) 2/7
c) 6/49
d) 1/7
e) 9/49
15. Si se lanza un dado, calcular la probabilidad de que se obtenga un número impar o
múltiplo de 3.
a) 1/2
b) 2/3
c) 1/3
d) 1/6
e) 5/6
16. Se extraen dos cartas, una tras otra, sin devolución, de una baraja de 40 cartas.
Calcular la probabilidad de que ambas cartas sean reyes.
a) 1/100
b) 1/5
c) 1/130
d) 23/130
e) 1/20
17. Se lanzan dos dados, ¿cuál es la probabilidad de que la suma de los resultados sea
menor que 6, si sabemos que dicha suma ha sido múltiplo de 4?
a) 1/3
b) 1/4
c) 5/18
d) 3/10
e) Ninguna de
las anteriores
18. Determinar la probabilidad de que al lanzar un dado cuatro veces no se obtenga ningún
6.
a) 0
b) 1/1296
c) 10/3
145
d) 2/3
e) 625/1296
19. En un naipe de 40 cartas se toman 3 cartas distintas. Calcular la probabilidad de que
sean números distintos.
a) 1/64.000
b) 3/40
c) 1/59.280
d) 4/3.705
e) 192/247
20. Se tiene dos urnas con bolas. La primera contiene 2 bolas blancas y 3 bolas negras;
mientas que la segunda contiene 4 bolas blancas y una bola negra. Si se elige una urna al
azar y se extrae una bola, ¿cuál es la probabilidad de que la bola extraída sea blanca?
a) 6/5
b) 8/25
c) 2/5
GGG
146
d) 3/5
e) 4/5