El algoritmo de división de polinomios explica con

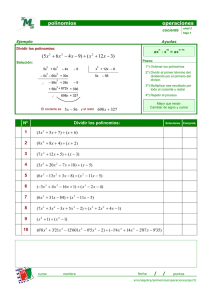
Algebra universitaria
UNIDAD III. POLINOMIOS
3.2. División de polinomios
División de polinomios:: El algoritmo de división de polinomios se
explica con el siguiente ejemplo:
Sea P(x)= x 4 − 5 x 3 + 11x 2 − 12 x + 6
Sea Q(x) = x 2 − 3 x + 3
(
(
(
) (
)
Dividir: x 4 − 5 x 3 + 11x 2 − 12 x + 6 ÷ x 2 − 3 x + 3
Puedes revisar el siguiente video en YouTube para la
división de polinomios:
http://www.youtube.com/watch?v=CDu3_SX3JLw
División sintética. Se ocupa para dividir un polinomio f(x) entre un
binomio de la forma “x – r”.
x5 + x 4 − 2 x 2 + 24
x+2
Solución: como el divisor corresponde al binomio x – r el cual en
este ejemplo es x + 2; el valor de r = -2 ya que al relacionar ambos
términos queda x – (-2)
Ejemplo: Usar la división sintética para dividir
La división queda:
x 2 − 2x + 2
2
x − 3x + 3 x 4 − 5 x 3 + 11x 2 − 12 x + 6
- x 4 + 3x 3 − 3 x 2
Dividiéndose de la siguiente manera:
− 2 x 3 + 8 x 2 − 12 x + 6
2x3 − 6x 2 + 6x
2x 2 − 6x + 6
- 2x 2 + 6x − 6
0
Otro ejemplo: Realizar la operación: 1 − a − a 5 - 3a 2 ÷ 1 + 2a + a 2
Solución:
− 3a 3 + 2a 2 − 3a + 1
2
− 3a 2 − a + 1
a + 2a + 1 − a 5
(
) (
)
El cociente queda: x 4 − x 3 + 2 x 2 − 6 x + 12
El residuo en este caso es: 0.
Puedes revisar el siguiente video en YouTube para la
división de sintética de polinomios:
http://www.youtube.com/watch?v=ABDvqk9ruzA
a 5 + 2a 4 + a 3
2a 4 + a 3 − 3a 2 − a + 1
− 2a 4 − 4a 3 − 2a 2
− 3a 3 − 5a 2 − a + 1
3a 3 + 6a 2 + 3a
a 2 + 2a + 1
− a 2 − 2a − 1
0
Elaboró: MC. Marcel Ruiz Martínez
1
Algebra universitaria
Teorema del residuo. Cuando un polinomio p(x) de grado al menos 1
es dividido entre un factor x – r, el residuo es p(r).
x 5 + x 4 − 2 x 2 + 24
Tomando el mismo ejemplo anterior.
x+2
Al dividir entre x – (-2) el residuo fue de cero.
Y al sustituir en la ecuación
p( x) = x5 + x 4 − 2 x 2 + 24
p(r = −2) = (−2)5 + (−2) 4 − 2(−2)2 + 24 = 0
p(-2) = 0 lo cual fue el mismo valor que el residuo.
Teorema del factor. “x – r” es un factor de p(x) si y solo si p(r) =0.
Para el polinomio: p(x) = x 5 + x 4 − 2 x 2 + 24
El binomio x + 2, o colocado de la manera x – (-2) es un factor
del polinomio p(x) dado que p(-2)=0
Práctica 3.2. División de polinomios. Para la lista de ejercicios
mostrados a continuación realice los siguientes:
i.
ii.
iii.
iv.
v.
21
23
25
27
33
Elabore una PRÁCTICA DE EJERCICIOS siguiendo las rubricas
correspondientes: http://marcelrzm.comxa.com/Rubricas/Rubricas.htm
Puede entregar impreso el trabajo o enviar el documento final por correo
electrónico a las siguientes direcciones: [email protected];
[email protected];
[email protected],
[email protected].
Colocar en ASUNTO: “Actividad 3.2. División de polinomios”
Elaboró: MC. Marcel Ruiz Martínez
2