operaciones combinadas con radicales

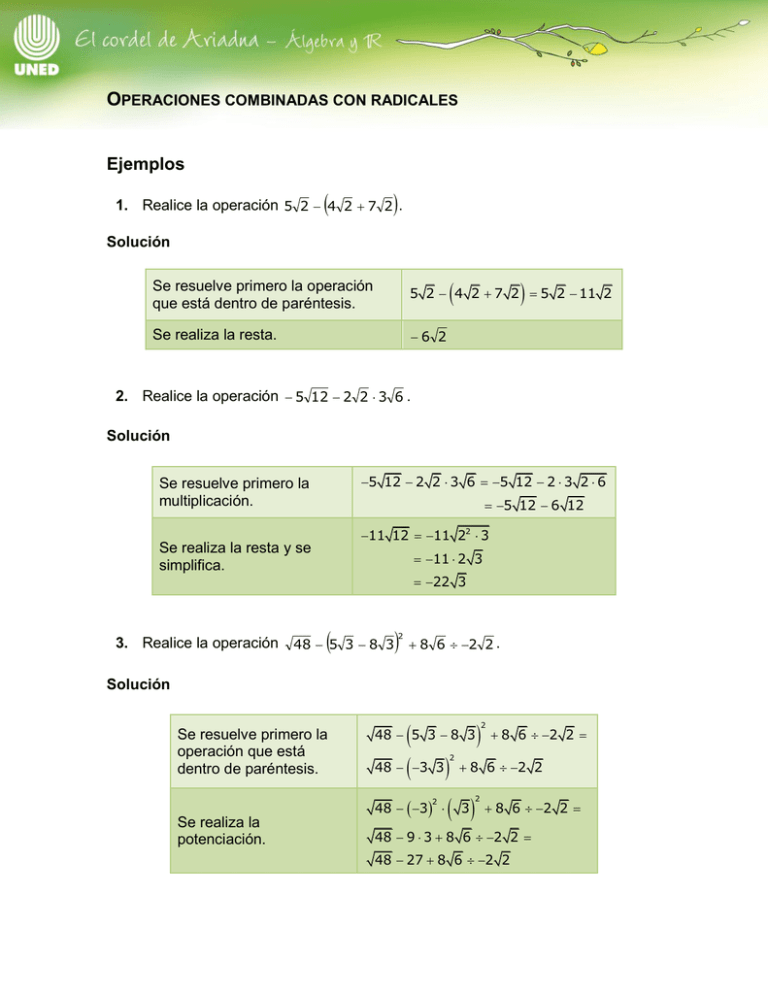
OPERACIONES COMBINADAS CON RADICALES
Ejemplos


1. Realice la operación 5 2  4 2  7 2 .
Solución


Se resuelve primero la operación
que está dentro de paréntesis.
5 2  4 2  7 2  5 2  11 2
Se realiza la resta.
6 2
2. Realice la operación  5 12  2 2  3 6 .
Solución
5 12  2 2  3 6  5 12  2  3 2  6
Se resuelve primero la
multiplicación.
 5 12  6 12
11 12  11 22  3
Se realiza la resta y se
simplifica.
 11  2 3
 22 3


2
3. Realice la operación 48  5 3  8 3  8 6  2 2 .
Solución
Se resuelve primero la
operación que está
dentro de paréntesis.

48   3 3 
48  5 3  8 3
2
48   3 
2
Se realiza la
potenciación.

2
 8 6  2 2 
 8 6  2 2
 3
2
 8 6  2 2 
48  9  3  8 6  2 2 
48  27  8 6  2 2
48  27   8  2 


6 2 
48  27  4 3 
Se efectúa la división y
se simplifica.
24  3  27  4 3 
22 3  27  4 3 
4 3  27  4 3
Se suman las
expresiones semejantes.

 27

4. Realice la operación 8 5 2  2 3  23 16  3 54 .
Solución


8 5 2  2 3  2 3 16  3 54 
Se resuelve primero la
multiplicación.


23 5 2  2 3  2 3 16  3 54 
23  5 2  23  2 3  2 3 16  3 54 
Luego se simplifican los
radicales.
5 24  2 23  3  2 3 24  3 2  33 
5  22  2  2 2  3  2  2 3 2  3 3 2 
20  4 6  4 3 2  33 2
Se suman los términos
que son semejantes.
20  4 6  73 2


5. Realice la operación  4 144  12  2 2  3 8  5 2 .
Solución


 4 144  12  2 2 3 8  5 2 
Se resuelve primero la
adición que está dentro
de paréntesis.


 4 144  12  2 2 3 22  2  5 2 

2  6

 4 144  12  2 2 3  2 2  5 2 
 4 144  12  2

2 5 2 
 4 144  12  2 2   2
Se realizan las
multiplicaciones en el
orden en que aparecen.
 4 2 4  32  2 2  3  2 2   2 
En la multiplicación
 4 144  12 , primero se
hacen homogéneos los
radicales.
 4 28  3 4  2 22 
 4 2 4  32  4 2 4  32  2 2   2 
 22  3  2  2 
8
Ejercicios
1. Resuelva las siguientes operaciones combinadas:
a)
3
4  33 2  3 2

b)  8 24  5 2 7 12  2 3

6  6 6  83 288
c)

2  34 2  4 32
d)

1
1
1


32
8
4
e)


4
2
f)  3 27 5 12  3 3  5 3

g)  2 18  3 8  2
h)
3
16  3 2  86 2
2
1
Soluciones
1. Resuelva las siguientes operaciones combinadas:
a)
3
4  33 2  3 2
3
4  33 2  3 2  3 4  3  13 2  2
 3 4  33 4
 23 4

2 7

3   8
b)  8 24  5 2 7 12  2 3
 8 24  5
12  2

24  5 2 7 22  3  2 3

2 14
 8 24  5 2 7  2 3  2 3
 8 24  5
3 2 3
 8 24  5 2  12 3
 8 24  5  12 2  3
 8 24  60 6
 8 22  2  3  60 6
 8  2 2  3  60 6
 16 6  60 6
 76 6
c)
6  6 6  83 288
6  6 6  83 288  6 6 3  6 6  83 288
 6 63  6  83 288
 6 6 4  83 288
 3 62  83 23  62
 3 62  8  23 62
 3 62  163 62
 153 36



d)

2  3

32  
2  34 2  4 32
4
24

2  34 2  4 2 4  2


2  34 2  24 2

2 42
 42 42
0
e)
1
1
1


32
8
4
1
1
1



32
8
4
1
1 1


32
8 4

1
1

32
2

1
1

2
2 2
4

1 1
1

4 2
2

3 1
4 2






2
f)  3 27 5 12  3 3  5 3
3 27 5 12  3 3
2

 5 3  3 27 5 22  3  3 3

2

 5 3
27 10 3  3 3   5 3
27 7 3   5 3
27 7   3   5 3
 3 27 5  2 3  3 3
 3
 3
 3
2
2
2
2
 3 27  49  3  5 3
 441 27  5 3
 441 32  3  5 3
 441  3 3  5 3
 1 323 3  5 3
 1 328 3


2
g)  2 18  3 8  2 4  1
2
2
 2 18  3 8  2 4   1   2 18  3  2 8  4   1




2
  2 18  6 24  2   1


2
  2 18  6  4 2   1


2
  2 18  24 2   1


2
  2 32  2  24 2   1


2
  6 2  24 2   1


2
  30 2   1


 1 800  1
 1 799
5 3
2
h)
3
16  3 2  86 2
3
16  3 2  86 2 
3
23  2  3 2  86 2
 23 2  3 2  86 2
 33 2  86 2
3

33  2  86 2
 6 33  2  86 2


1 6 33  2
8
2
6
27
8