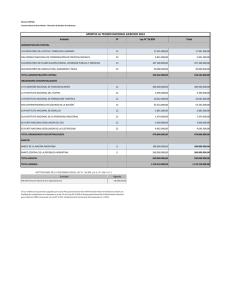
Control de velocidad del sistema motor hps5130

INSTITUTO TECNOLÓGICO DE COSTA RICA
II SEMESTRE 2013
ESCUELA DE INGENIERIA EN ELECTRÓNICA
CURSO: EL-5409 LABORATORIO DE CONTROL AUTOMÁTICO
MEDIO: Proyecto corto 2
FECHA: 6 de septiembre de 2013
PROF: Ing. Eduardo Interiano
PROYECTO CORTO 2
Tema: Control de velocidad angular del motor CD hps5130.
Figura 1: Fotografía del sistema de velocidad angular hps5130
Requisitos: Computador con Matlab instalado, regulador digital PI ajustable.
Descripción del trabajo:
En el proyecto corto 1, se obtuvo un modelo empírico de velocidad del motor hps5130 con un
experimento cuyos datos fueron capturados con un osciloscopio InfiiniVision y luego procesados
con la herramienta ident de Matlab, la figura 2 muestra los datos adquiridos. Para este proyecto 2,
su tarea consiste en utilizar la herramienta sisotool de Matlab para diseñar un regulador PI
discreto adecuado para el motor que haga que el sistema se estabilice en 150ms; verificar el
diseño usando simulink y realizar un control de velocidad angular constante, capaz de eliminar el
efecto de las perturbaciones introducidas.
9
Entrada [V]
Velocidad [krpm]
8
7
6
5
4
3
2
1
0
-1
-1
-0.5
0
0.5
1
1.5
2
2.5
3
3.5
4
Figura 2: Captura de la entrada [V] y la velocidad angular [krpm] del sistema motor hps5130.
Con la entrada medida directamente en el motor (después del amplificador de potencia, datos
procesados para representar la velocidad del motor CD en krpm).
Parte I: Descripción del entorno del regulador PI discreto
Objetivo: Conocer el entorno del regulador PI discreto
1
1
Figura 2: Estructura del regulador PI discreto
R(z)
0.5
+
PI (z )
2.4
Motor (s )
Ω(z)
‐
0.5
GO(z)
Figura 3: Diagrama de control del servomotor hps5130
Se utilizará la planta hps5130, controlando con una señal de 0-5 V el motor; por lo cual
estaremos usando el amplificador integrado el cual tiene una ganancia de 2.4 desde la entrada de
5V. El sistema microprocesador a utilizar puede únicamente medir y generar señales de 0-5V; por
Laboratorio de Control Automático
Proyecto corto 2
Pág. 2
lo que introducimos los atenuadores de 0.5 en el sistema, éstos están incorporados en el regulador
digital a utilizar, de tal manera que señales de hasta 10V producidas por el tacómetro sean
presentadas a la entrada de ADC del sistema microprocesador como señales de hasta 5V como se
muestra en la figura 3.
En la figura 4 se muestra el sistema equivalente, con realimentación unitaria, y para el cual se
diseñará el regulador PI digital.
R(z) +
PI (z )
1.2
Ω(z)
motorCD (z )
‐
Gˆ O ( z )
Figura 4: Diagrama de control discreto simplificado del sistema motor hps5130
Parte II: Diseño y simulación de un control PI para el motor CD
Objetivo: Calcular un regulador PI para el motor CD que elimine las perturbaciones
Se discretizará la planta con un tiempo de muestreo de 5ms, dado por la condición de
estabilización requeridas de 150ms y que corresponde a 30 periodos de muestreo durante el
tiempo de estabilización (valores usuales van de 32 a 40 periodos de muestreo durante el tiempo
de estabilización y por limitaciones del sistema microprocesador se ajustó a T = 5ms).
Procedimiento:
Paso 1) En Matlab cree primero la variable "s" con la orden tf('s'). Luego escriba el modelo
obtenido para el motor CD en el proyecto corto 1 (use este modelo, que es similar al obtenido por
el grupo durante el proyecto 1):
30.38
24
Paso 2) Discretice el modelo del motor CD por el método del retenedor de orden cero y con un
periodo T = 5ms con la orden de Matlab siguiente, (el método por defecto es retenedor de orden
cero o ZOH, así que puede omitir el tercer parámetro si lo desea):
motorCDz = c2d(motorCD,0.005,'zoh')
Laboratorio de Control Automático
Proyecto corto 2
Pág. 3
Paso 3) Escale el modelo por el factor 1.2 para obtener el modelo de la planta hps5130 visto
desde la entrada de 5V, como se muestra en la figura 4, que incorpora la ganancia del
amplificador y la de los atenuadores de señal mostrados en la figura 4.
motorCDz = motorCDz * 1.2
Paso 4) En Matlab, ejecute la orden sisotool('rlocus', motorCDz).
Paso 5) Coloque el requisito de diseño correspondiente al tiempo de estabilización en la ventana
del sisotool con clic derecho sobre el área blanca y luego seleccionando un nuevo requisito de
diseño. El tiempo de estabilización del 2% será de 150ms, como se muestra en la figura 5, esta
condición de diseño es representada por un círculo de radio 0.875 dentro del círculo unitario.
Paso 6) Agregue un regulador PI formado por un polo en z = 1 y un cero en los alrededores del
polo dominante del sistema en lazo abierto, (un poco a la izquierda, sobre, o un poco a la
derecha). Puede editar el compensador de forma gráfica, arrastrando con el ratón; o en la ventana
de edición del compensador, dando clic derecho en el área blanca y escribiendo el valor del polo
o cero numéricamente.
Figura 5: Ajuste de la ganancia del regulador PI en Sisotool
Paso 7) Ajuste la ganancia. Puede hacerlo de forma gráfica arrastrando el polo del sistema a la
región deseada, dentro del círculo que define el tiempo de estabilización, para obtener un sistema
resultante con un tiempo de estabilización del 2% menor a 150ms, como se muestra en la figura
5, y con cero error de estado estacionario (debido al aumento del tipo de sistema de 0 a 1
Laboratorio de Control Automático
Proyecto corto 2
Pág. 4
efectuado por el integrador). Para ello observe, mientras arrastra el polo en el área del lugar de las
raíces, la simulación del sistema mostrada en la figura 6.
Step Response
1
0.9
0.8
0.7
Amplitude
0.6
0.5
0.4
0.3
0.2
0.1
0
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
Time (sec)
Figura 6: Simulación en sisotool del control con PI para la planta hps5130.
Paso 8) Cuando haya finalizado con la sintonización del regulador PI, exporte el diseño en
Sisotool al entorno de Simulink como se muestra en la figura 5. Responda si a la pregunta de si
desea escribir al entorno de Matlab las variables del diseño. Estas variables son llamadas F, H, C
y G para el pre-regulador, el sensor, el regulador y la planta respectivamente.
Paso 9) Luego simule su sistema regulado con PI en Simulink y verifique que se mantiene el
sistema bien compensado aun en presencia de perturbaciones de entrada y de salida (relativas a la
planta).
Paso 10) Finalmente descomponga el regulador en forma paralela usando la función residuez de
Matlab y luego simule en Simulink el compensador PI así obtenido. Verifique como en el paso 7.
Vea la figura 7 para una implementación paralela de un PI discreto. Las constantes mostradas Kp
y Ki representan las que Ud. habrá encontrado en el paso 7 y que habrá exportado en el paso 8.
Figura 7: Implementación de un regulador PI discreto en forma paralela.
Laboratorio de Control Automático
Proyecto corto 2
Pág. 5
6
5
4
3
2
Entrada [V]
Velocidad [krpm]
Acción de control [V]
1
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Figura 8: Simulación de entrada escalón en 0.1s y de perturbaciones en 0.5s y 0.7s
(Note que Simulink produce figuras con el fondo negro. Para graficar con el fondo blanco debe
exportar los datos y luego graficarlos con la orden plot de Matlab.)
Parte III: Implementación del diseño en el sistema microprocesador
Paso 1: Escalar las constantes Kp y Ki obtenidas en la etapa anterior. En el sistema
microprocesador se pueden ajustar las dos constantes con ayuda de dos potenciómetros, cuyos
valores de tensión son convertidos de analógico a digital por un ADC de 8 bits que puede
procesar valores entre 0 y 5V. La ganancia proporcional máxima representable Kp_máx = 1
corresponde a 5V, y la ganancia integral máxima, Ki_máx. = 0.2 corresponde a 5V; por lo que
deberá hacer una regla de tres para obtener el valor de tensión correspondiente a sus constantes
según el ejemplo siguiente y tomando los valores correspondientes de la tabla 1:
Kx[V] = Kx * Umáx/Kx_máx
Tabla 1: Relaciones de los potenciómetros de ajuste
Constante Umáx [V]
Kx_máx
Kp
5
1
Ki
5
0.2
Paso 2: Ajuste de los valores de Kp y Ki en el regulador digital. Con ayuda de un voltímetro de
CD, mida la tensión del cursor de cada uno de los potenciómetros de ajuste de constantes,
mientras varía el potenciómetro hasta obtener el valor calculado en la etapa de escalado.
Paso 3: Medición de la respuesta ante un escalón y ante perturbaciones del sistema regulado.
Utilice un osciloscopio para medir la entrada escalón de velocidad al sistema, con el canal 1 y la
respuesta de velocidad angular, con el canal 2. Ajuste la escala de tiempo a 100ms por división y
las escalas de amplitudes a 2V por división. El canal 1 será el disparador por flanco positivo.
Ajuste el punto de disparo en la segunda división horizontal para que pueda ver todo el evento.
Laboratorio de Control Automático
Proyecto corto 2
Pág. 6
Aplique un escalón de 4000rpm al sistema presionando el pulsador. También puede aplicar
perturbaciones al sistema, conmutando la carga, (una bombilla incandescente), aplicada a la
salida del generador
Figura 9: Captura de la respuesta del sistema hps5130 regulado con un PI digital, ante un escalón
equivalente a 4000 rpm (4V) y ante perturbaciones.
En la figura 9 se puede apreciar la respuesta de velocidad del sistema motor CD, (canal 2, verde),
ante una entrada escalón en la referencia equivalente a 4000 rpm, (canal 1, amarillo). Note que la
señal escalón no está a escala, tiene una amplitud de 5V, ya que se trata de una señal de
referencia digital que indica únicamente el momento en el cual se aplica el escalón; el valor del
escalón está determinado internamente por el sistema digital y ajustado al equivalente de
4000rpm. Analizando la gráfica podemos determinar que el tiempo de estabilización es
ligeramente inferior a 150ms; que el error de estado estacionario es cero; y que el regulador PI
utilizado es capaz de cancelar las perturbaciones aplicadas al sistema y que lo hace en
aproximadamente 150ms. Por lo que podemos dar por concluido el diseño e implementación.
Los resultados deben enviarse a más tardar el 14 de septiembre 2013 al correo electrónico
[email protected], con todos los documentos y archivos creados para resolver el problema.
Referencias
[1] http://www.ie.itcr.ac.cr/einteriano/control/Laboratorio/ProyectosCortos/ProyectoCorto1_II_2013.pdf
EIS/eis
2013
Laboratorio de Control Automático
Proyecto corto 2
Pág. 7