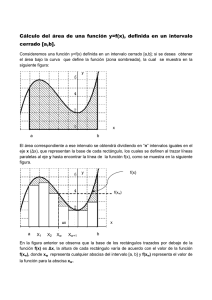
El cálculo integral tiene una estrecha relación con el

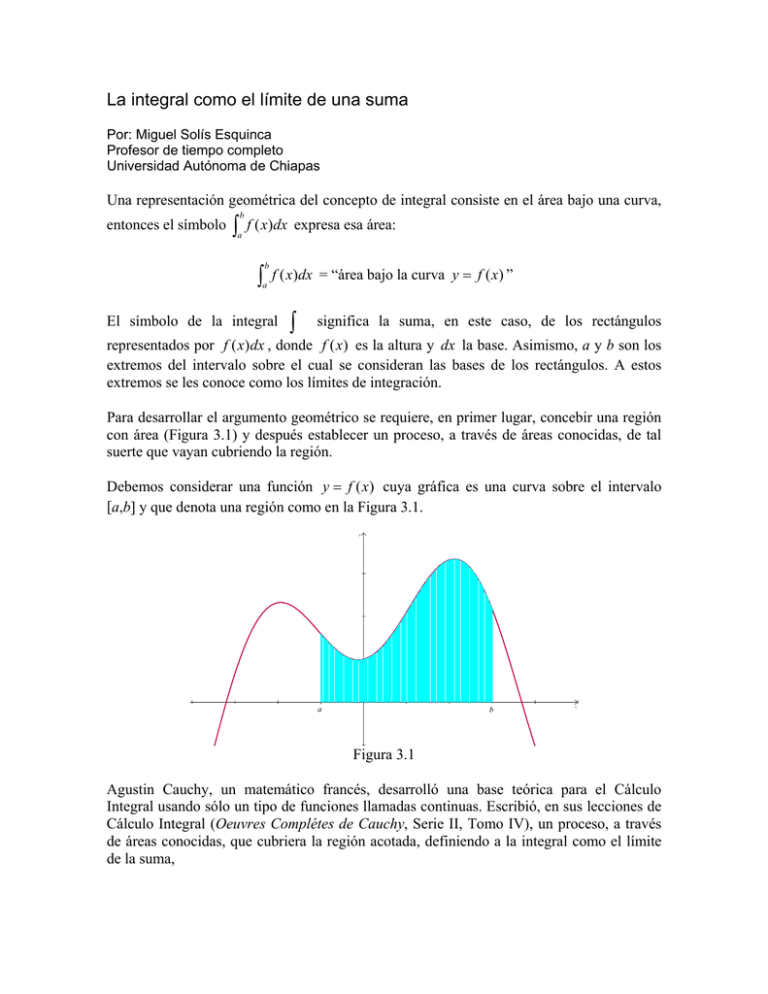
La integral como el límite de una suma
Por: Miguel Solís Esquinca
Profesor de tiempo completo
Universidad Autónoma de Chiapas
Una representación geométrica del concepto de integral consiste en el área bajo una curva,
entonces el símbolo
∫
b
a
f ( x)dx expresa esa área:
∫
b
a
f ( x)dx = “área bajo la curva y = f (x) ”
El símbolo de la integral
∫
significa la suma, en este caso, de los rectángulos
representados por f ( x)dx , donde f (x) es la altura y dx la base. Asimismo, a y b son los
extremos del intervalo sobre el cual se consideran las bases de los rectángulos. A estos
extremos se les conoce como los límites de integración.
Para desarrollar el argumento geométrico se requiere, en primer lugar, concebir una región
con área (Figura 3.1) y después establecer un proceso, a través de áreas conocidas, de tal
suerte que vayan cubriendo la región.
Debemos considerar una función y = f ( x) cuya gráfica es una curva sobre el intervalo
[a,b] y que denota una región como en la Figura 3.1.
y
a
b
x
Figura 3.1
Agustin Cauchy, un matemático francés, desarrolló una base teórica para el Cálculo
Integral usando sólo un tipo de funciones llamadas continuas. Escribió, en sus lecciones de
Cálculo Integral (Oeuvres Complétes de Cauchy, Serie II, Tomo IV), un proceso, a través
de áreas conocidas, que cubriera la región acotada, definiendo a la integral como el límite
de la suma,
n
lim ∑ f ( xi )∆xi
n →∞
i =1
La estrategia consistió en dividir al intervalo [a, b], el dominio de la función f (x) , en n
subintervalos de longitudes x1 − a , x2 − x1 , x3 − x2 , … , b − xn −1 . La longitud de cada
subintervalo (base) se multiplica por el valor de la función correspondiente a su primer
punto (altura), así x1 − a se multiplica por f (a) , x2 − x1 por f ( x1 ) , x3 − x2 por f ( x2 ) , …
, b − xn −1 por f ( xn −1 ) . Para obtener el valor del área total se suman todas las áreas de los
rectángulos, la suma correspondiente se expresa por
S = ( x1 − a) f (a ) + ( x2 − x1 ) f ( x1 ) + K + (b − xn −1 ) f ( xn −1 )
S representa, geométricamente, una aproximación al área bajo la curva y = f (x) en el
intervalo [a, b] (Figura 3.2).
y
a
x
1
x
2
x
x
3
n-1
b
x
Figura 3.2
La suma S depende de f (x) y de la forma de la partición, es decir, depende del número de
subintervalos en los que se ha dividido al intervalo [a, b] y de las longitudes de éstos, ya
que pueden tener longitudes iguales o no. De esta manera la suma S cambia cuando el
número de divisiones de [a, b] crece considerablemente, toda vez que el tamaño de las
divisiones disminuye también considerablemente. Sin embargo Cauchy muestra que el
límite de la suma S es independiente de la forma de la división y de la división misma, es
decir, cuando el número de divisiones de [a, b] tiende a infinito, el tamaño de todas las
divisiones tiende a cero.
En este sentido la notación
∫
b
a
f ( x)dx indica explícitamente que el límite de S depende del
intervalo [a, b] y de la función f (x) .
Así, el límite de la suma S tiende a ser el área
∫
b
a
f ( x)dx :
b
“ S ⎯n⎯
⎯→ ∫ f ( x)dx ”
→∞
a
Y geométricamente, significa que el límite de S es el área bajo la curva y = f (x) (Figura
3.3).
y
y
⎯n⎯
⎯→
→∞
a
x
1
x
2
x
x
3
n-1
b
a
b
Figura 3.3
El intervalo [a, b] es el dominio de la función f (x) y de la suma S. Los extremos del
intervalo a y b son los límites de integración y el límite de la suma S, cuando n tiende a
infinito, suele expresarse de la siguiente manera:
n
lim ∑ f ( xi )∆xi , (si n → ∞ , ∆xi → 0 ),
n →∞
i =1
donde
n indica el número de divisiones del intervalo [a, b].
∆xi indica la longitud de cualquier subintervalo de [a, b]: xi +1 − xi , y
n
∑
i =1
indica la suma de los n términos de la forma f ( xi )∆xi
Así
n
b
i =1
a
lim ∑ f ( xi )∆xi = ∫ f ( x)dx
n→∞