1.1 Area de una funcion y=f_x_

Cálculo del área
rea de una
una función y=f(x), definida en u
un intervalo
cerrado [a,b].
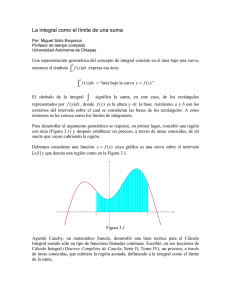
Consideremos una función y=f(x) definida
a en un intervalo cerrado [a,b]; si se desea obtener
el área bajo la curva que define la función (zona sombreada), la cual se muestra en la
siguiente figura:
y
x
a
b
El área correspondiente a ese intervalo se obtendrá dividiendo en ““n”” intervalos iguales en el
eje x (∆x),
x), que representan la base de cada rectángulo,
rectángulo, los cuales se definen al trazar líneas
paralelas al eje y hasta encontrar la línea de la función f(x), como se muestra en la siguiente
figura.
y
f(x)
f(xw)
x
∆X
a
X1
X2
Xw
Xw+1
b
En la figura anterior se observa que la base de los rectángulos trazados por debajo de la
función f(x) es ∆x,, la altura de cada rectángulo varía de acuerdo con el valor de la función
f(xw), donde xw representa cualquier abscisa del intervalo [a, b] y f(xw) representa el valor de
la función para la abscisa xw.
Finalmente el área total bajo la curva se obtiene sumando el área de todos los rectángulos
en los que se dividió el intervalo [a, b], que en nuestra figura fueron 7.
A= { (∆x)(fx1)+ (∆x)(fx2)+ (∆x)(fx3)+ (∆x)(fx4)+ (∆x)(fx5)+ (∆x)(fx6)+ (∆x)(fx7)}
La expresión anterior se puede representar de la siguiente manera:
A=∑
(
)(∆ )
El símbolo Σ (sigma) es una letra que pertenece al abecedario Griego y en matemáticas se
emplea para representar la sumatoria de varios elementos.
Para poder determinar el área bajo la curva descrita por una función f(x), se deberán
seguir los siguientes pasos.
1.- Dividir al intervalo [a, b] en “n” subintervalos, esto representará la medida de la base de
los rectángulos (∆ ). Para ello utiliza la siguiente expresión:
−
∆ =
2.- Encontrar el valor de las abscisas ( ) de cada uno de los rectángulos, haciendo que los
sean los lados derechos de cada rectángulo. Al primer valor lo llamaremos =a, para
determinar los demás valores de
se utilizará la siguiente fórmula:
=
+ ( )(∆ )
Donde w representa la posición de la línea que delimita al lado derecho de los rectángulos, a
partir del valor de a en el intervalo considerado.
3.- Encontrar el valor de la altura de cada uno de los rectángulos, esta altura la obtendremos
al sustituir los valores de
,
,
,…
, en la función f(xw).
4. Encontrar el área total bajo la curva que define f(x), para ello aplicamos los resultados
obtenidos en los pasos anteriores en la fórmula:
A=∑
(
)(∆
)
Ejemplos resueltos.
Ejemplo1.. Calcular el área total que se encuentra debajo de la función
función y=f(x)= 2x+3, en el
intervalo de [-1, 5],, dividiéndolo en n= 6 rectángulos.
Paso 1.
1
1
1
1
1
1
1
∆
∆
∆
5
1
6
5
1
6
!
6
6
"
1
Paso 4. A=∑
#
$
Paso 2.
∆
0 1 =-1+0=-1
1 1 =-1+1=0
2 1 =-1+2=1
3 1 =-1+3=2
4 1 =-1+4=3
5 1 =-1+5=4
6 1 =-1+6=5
Paso 3.
3
f(xw)= 2x+3
f(x1)= (2)(x1)+3=(2)(0)+3=0+3=3
f(x2)= (2)(x2)+3=(2)(1)+3=2+3=5
f(x3)= (2)(x3)+3=(2)(2)+3=4+3=7
f(x4)= (2)(x4)+3=(2)(3)+3=6+3=9
)+3=(2)(
f(x5)= (2)(x5)+3=(2)(4)+3=8+3=11
f(x6)= (2)(x6)+3=(2)(5)+3=10+3=13
∆
A=(3)(1)+(5)(1)+7(1)+(9)(1)+(11)(1)+(13)(1)=3+5+7+9+11+13=48u
(3)(1)+(5)(1)+7(1)+(9)(1)+(11)(1)+(13)(1)=3+5+7+9+11+13=48u2
f(x)=2x+3
Nota: Se puede observar en la gráfica
que el valor del área delimitada por los
rectángulos es mayor al valor real del
área que se encuentra debajo de la
función, sin embargo es una buena
aproximación y en la medida en que el
∆x sea más
ás pequeño el error será
menor.
x
Ejemplo 2.. Calcular el área total que se encuentra debajo de la función y=f(x)= x2+2, en el
intervalo de [-2, 3],, dividiéndolo en n= 9 rectángulos.
Paso 1.
∆
∆
∆
3
2
9
2
Paso 2.
∆
#
0
=-2+0=-2
2
1
2
!*
#
+
+
= 0.55
Paso 4. A=∑
2
!
2
3
"
2
4
#
2
5
$
2
6
,
2
7
-
2
8
+
2
9
+
#
+
#
+
#
+
#
+
#
+
#
+
#
+
#
+
#
+
Paso 3.
2
f(xw)= x +2
#
!
+
+
-
=-2+ =
=-2+
+
#
=-2+
+
=-2+
=-2+
=-2+
=-2+
=-2+
=-2+
+
#
+
!
+
!#
+
"
+
"#
+
=
+
!
=
=
=
=
=
=
+
+
,
+
+
,
) +2= 4.08
+
- 2
f(x2)= (x2)2+2=
2=(
) +2= 2.79
+
! 2
) +2=
+
f(x3)= (x3)2+2=
2=(
2.11
f(x4)= (x4)2+2=
2=( )2+2= 2.04
f(x5)=
+
, 2
(x5) +2=
2=( + ) +2=
2
f(x6)= (x6)2+2=
2=(
+
f(x7)= (x7)2+2=
2=(
+
f(x8)= (x8)2+2=
2=(
=3
! 2
f(x1)= (x1)2+2=
2=(
2.6
)2+2= 3.77
+
, 2
) +2=
+
+
5.56
)2+2= 7.97
f(x9)= (x9)2+2=
2=( 3 )2+2= 11
∆
A=(4.08)(0.55)+(2.79)(0.55)+(2.11)(0.55)+(2.04)(0.55)+(2.6)(0.55)+(3.77)(0.55)+(5.56)(0.55)+
(4.08)(0.55)+(2.79)(0.55)+(2.11)(0.55)+(2.04)(0.55)+(2.6)(0.55)+(3.77)(0.55)+(5.56)(0.55)+
(7.97)(0.55)+ (11)(0.55)= 23.05u2
f(x)=x2+2
Nota: Se puede observar en la gráfica
que el valor del área delimitada por los
rectángulos es ligeramente mayor al
valor real del área que se encuentra
debajo de la función, sin embargo es una
buena aproximación y en la medida en
que el ∆x sea más
ás pequeño
peq
el error será
menor.
x
Ejemplo 3.. Calcular el área total que se encuentra debajo de la función y=f(x)= x3+4x2-3, en
el intervalo de [-3, 0],, dividiéndolo en n= 12 rectángulos.
Paso 1.
∆
∆
∆
0
3
12
!
"
3
Paso 2.
∆
0
= -3+0=-3
3
1
3
= 0.25
3
!
3
"
3
#
3
$
3
,
3
-
3
+
3
3
3
Paso 4. A=∑
Paso 3.
f(xw)= x +4x -3
3
2
"
"
2
"
= -3+ =
"
f(x1)= (
"
+
f(x2)= (
f(x3)= (
"
"
"
,
f(x4)= (
#
"
$
f(x5)= (
$
"
#
f(x6)= (
,
"
"
f(x7)= (
-
"
!
f(x8)= (
+
"
"
f(x9)= (
"
= -3+ " =
!
3
"
4
"
5
"
6
"
7
"
8
"
9
"
10
11
12
= -3+ " =
=-3+ " =
=-3+ " =
=-3+ " =
=-3+ " =
=-3+ " =
=-3+ =
"
"
"
=-3+
=-3+
=-3+
"
"
"
=
=
=0
"
f(x10)= (
"
f(x11)= (
)3+(4)(
+
"
2
)3+(4)(
+
"
+ 3
) +(4)(
(4)(
"
- 3
-3= 6.45
"
2
-3= 6.37
"
+ 2
-3= 5.85
) +(4)(
(4)(
"
- 2
-3=
"
, 2
5
) +(4)(
(4)(
"
$ 2
-3=
"
# 2
2.62
) +(4)(
(4)(
"
" 2
-3=
"
! 2
0
"
, 3
) +(4)(
(4)(
"
$ 3
"
# 3
) +(4)(
(4)(
"
" 3
"
! 3
) +(4)(
(4)(
"
"
"
3
-3= 3.89
-3= 1.29
"
)3+(4)(
+
-3= -1.17
2
"
)3+(4)(
+
-3= -2.12
2
"
-3= -2.76
2
f(x12)= (0 ) +(4)(
(4)(0 -3= -3
∆
A=(6.45)(0.25)+(6.37)(0.25)+(5.85)(0.25)+(5)(0.25)+(3.89)(0.25)+(2.62)(0.25)+(1.29)(0.25)+
(6.45)(0.25)+(6.37)(0.25)+(5.85)(0.25)+(5)(0.25)+(3.89)(0.25)+(2.62)(0.25)+(1.29)(0.25)+
(0)(0.25)+ (-1.17)(0.25)+ (-2.12)(0.25)+
2.12)(0.25)+ (-2.76)(0.25)+ (-3)(0.25)=
3)(0.25)= 5.60 u2
f(x)=x3+4x2-3
Nota: En este tipo de problemas el área
total que se desea conocer se obtiene
restando al área que está por debajo de
la función (rectángulos obscuros) el área
que está por encima de la función f(x)
(rectángulos rayados).
x