74 9) Cubo-octaedro de Arquímedes Se calcula la medida de la

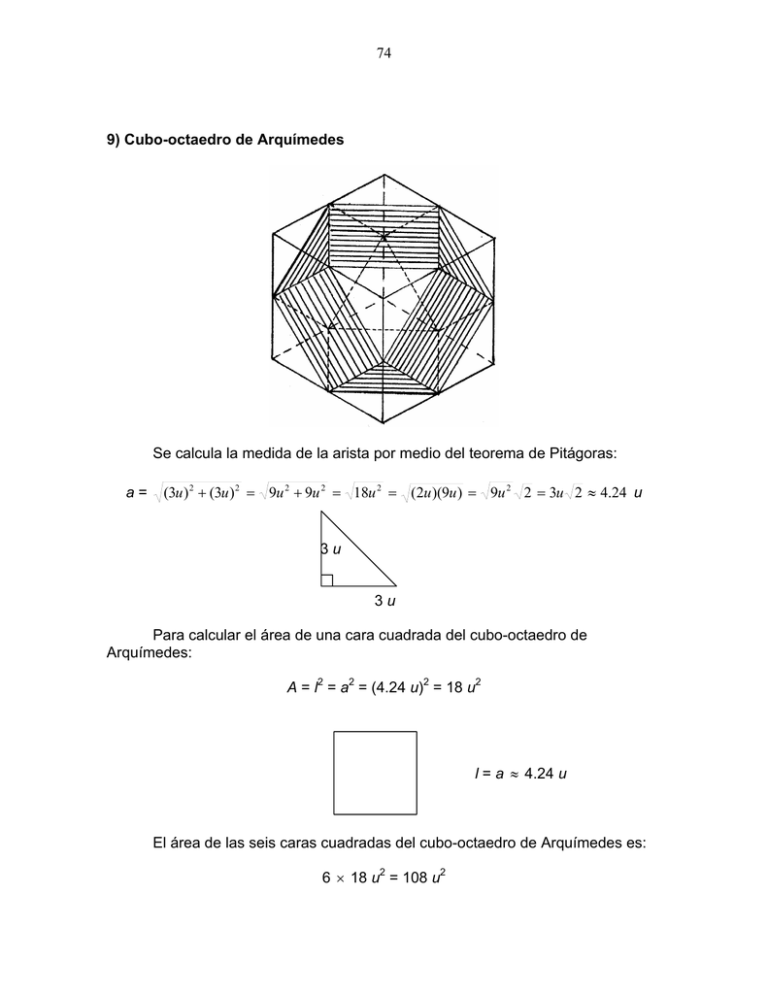
74
9) Cubo-octaedro de Arquímedes
Se calcula la medida de la arista por medio del teorema de Pitágoras:
a=
(3u ) 2 + (3u ) 2 = 9u 2 + 9u 2 = 18u 2 = (2u )(9u ) = 9u 2 2 = 3u 2 ≈ 4.24 u
3u
3u
Para calcular el área de una cara cuadrada del cubo-octaedro de
Arquímedes:
A = l2 = a2 = (4.24 u)2 = 18 u2
l = a ≈ 4.24 u
El área de las seis caras cuadradas del cubo-octaedro de Arquímedes es:
6 × 18 u2 = 108 u2
75
El área de una cara triangular del cubo-octaedro de Arquímedes es:
A=
bh
2
Conocemos la base, pero no la altura.
Para calcular la altura del triángulo se aplica el teorema de Pitágoras:
h=
(4.24u ) 2 − (2.12u ) 2 = 18u 2 − 4.5u 2 = 13.5u 2 ≈ 3.67 u
a = l ≈ 4.24 u
h
l/2
l 4.24u
≈
≈ 2.12 u
2
2
El área de la cara triangular del cubo-octaedro de Arquímedes es:
A=
(4.24u )(3.67u )
bh
≈
≈ 7.8 u2
2
2
El área de las ocho caras triangulares del cubo-octaedro de Arquímedes es:
8 × 7.8 u2 ≈ 62.35 u2
El área total del cubo-octaedro de Arquímedes es la suma de las áreas de
las caras cuadrangulares y las caras triangulares:
A ≈ 108 u2 + 62.35 u2 ≈ 170.35 u2
Para calcular el volumen del cubo-octaedro de Arquímedes se resta al
volumen total del geoespacio el volumen de las ocho pirámides triangulares que
se forman en los vértices del geoespacio.
El geoespacio es un cubo de 6 u de arista y su volumen es: V = a3 = (6 u)3
= 216 u3
76
Para calcular el volumen de una pirámide triangular se recurre a los
siguientes dibujos:
3u
4.24 u
H=3u
h=3u
3u
b=3u
El área de la base es:
Ab =
bh (3u )(3u ) 9u 2
=
=
= 4.5 u2
2
2
2
El volumen de la pirámide es:
A h (4.5u 2 )(3u )
= 4.5 u3
V= b =
3
3
El volumen de las ocho pirámides es 8 x 4.5 u3 = 36 u3
Para calcular el volumen del cubo-octaedro:
VCO = VG – VP = 216 u3 – 36 u3 = 180 u3
Para manejar fracciones comunes pueden calcularse algunas relaciones de
volumen; por ejemplo, la relación existente entre el volumen del cubo-octaedro de
Arquímedes y el del geoespacio es:
VCO 180u 3 5u 3
R=
=
=
≈ 0.833
VG
216u 3 6u 3