6 Integración

6
Integración
6.1
Integral Indefinida
Antes de comenzar este capítulo, el lector debería releer la sección 3.3. La daremos por conocida
y continuaremos desde allí nuestro razonamiento.
Primitivas
No sabemos si, dada una función f en un intervalo abierto (finito o infinito) I, existe
alguna solución de la E.D.
dy
= f (x) ,
x ∈ I.
(1)
dx
Sí sabemos que, en caso de existir una función F solución de (1), también son soluciones todas
las funciones F +C con C constante y ninguna otra. En esta sección desarrollaremos técnicas
(algebraicas) para encontrar tales soluciones. Una función F cuya derivada es f en cierto
intervalo es llamada una primitiva o una integral indefinida de f en ese intervalo. Si pensamos
la búsqueda de primitivas como una operación, nos encontraremos en una situación atípica: una
operación cuyo resultado no es único. Nos hemos acostumbredo a que el símbolo "4 + 3" que
indica la operación de sumar esos números, ya que se escribe el resultado como "4 + 3 = 7",
pase a ser una manera alternativa de designar al número 7. El igual, en Matemática, significa
identidad. Dos objetos conectados por el signo "=" son el mismo objeto escrito de dos maneras
distintas. Este principio es el que asegura la regla de sustitución: en una fórmula, un término
se puede reemplazar por otro que sea igual. Si vamos a admitir un símbolo para la operación de
buscar primitivas, deberemos
tener el cuidado de no confundirlo con el resultado.
La tradición
R
R
estableció el símbolo
para
la
operación
de
buscar
primitivas.
Se
escribe
f
(sin
mención
R
de la variable) o
f (x) dx (mencionando la variable). Este símbolo denota la operación de
buscar una primitiva de la función f. Así, por ejemplo,
Z
cos = sin,
Z
1 3
x .
x2 dx =
3
Pero también
Z
Z
cos = sin +1 y
x2 dx =
1 3
x + 32.
3
R
Como se ve, si el signo ” = ” se entiende de la manera habitual, si se piensa que ” cos ”
es una función (ya que se presenta igualada a sin que sí lo es), puesto que dos cosas iguales
Capítulo 6. Integración
a una tercera son iguales entre
que sin = sin +1. Debemos entonces tener la
R sí, concluiremos
R
precaución de entender que f y f (x) dx son operaciones y que
Z
f (x) dx = F (x) en I significa que F 0 (x) = x, ∀x ∈ I.
(2)
El elemento ”dx” que se lee diferencial equis, que aparece "multiplicando" en el miembro
de la izquierda, no tiene significado en sí mismo. La integración es una operación inversa de
la derivación y el rol del dx multiplicando en la integración tiene un papel y una historia
similares a los del dx dividiendo en la diferenciación que se aclarará más adelante. Nuestro
conocimiento de que las primitivas de una función f forman una familia de funciones en la
que dos miembros difieren en una constante se suele recoger escribiendo, cuando F es una
primitiva cualquiera,
Z
f (x) dx = F (x) + C.
Nótese que la insistencia en referir el concepto de primitiva a un intervalo no es caprichosa.
El teorema de unicidad en la sección 3.3. tiene validez en un intervalo. Si aceptamos otro tipo
de dominios, dos primitivas podrían no diferir en una constante. En algunos libros se puede
encontrar que
Z
1
dx = ln |x| .
(3)
x
En efecto, ambas funciones tienen su dominio en Ω = (−∞, 0) ∪ (0, +∞) y, en ese conjunto,
d
1
dx ln |x| = x . Pero Ω no es un intervalo y no aceptaremos aquí la fórmula (3).
A partir de las derivadas que conocemos podemos construir una primera tabla de integrales
inmediatas. Luego veremos técnicas para calcular otras integrales más complicadas a partir de
ellas (ver ejercicio 1.).
Z
Z
Z
xc dx =
x−1 dx = ln x + K
para c 6= −1
en (0, +∞) ,
x−1 dx = ln (−x) + K
Z
Z
Z
xc+1
+ K,
c+1
en (−∞, 0) .
sin x dx = − cos x + C
cos x dx = sin x + C
dx
√
= arcsin x + C, en (−1, 1)
2
1
−
x
Z
ex dx = ex + C
136
6.1 Integral indefinida
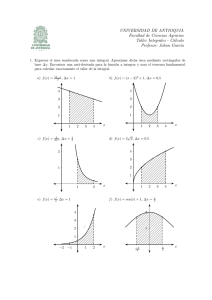
Ejercicios:
1. Calcular las siguientes integrales indefinidas. En los casos que corresponda explicitar el
intervalo de validez de la respuesta dada.
R 1
R
n∈Z
b) x n dx,
n ∈ Z, n 6= 0
a) xn dx,
c)
e)
g)
i)
R
R
R
R
sin xdx
d)
R
cos xdx
R
f) (1 + tan2 x)dx
1
cos2 x dx
√ 1
dx
1−x2
h)
ex dx
j)
R
R
√ −1 dx
1−x2
dx
x
2. Mostrar un ejemplo de una función con dos primitivas que no difieren en una constante
(Obviamente en una región Ω que no es un intervalo)
Cada propiedad de la derivación se convierte en una propiedad de su operación inversa: la
integración indefinida. Ellas serán de gran utilidad en el cálculo de primitivas.
Linealidad
R
R
Usando la linealidad de la derivada, si
f = F y R g = G en un intervalo, y λ, µ son
constantes, (λF + µG)0 = λF 0 + µG0 = λf + µg. Esto es, λf + µg = λF + µG. Este resultado
se recuerda escribiéndolo así:
Z
Z
Z
λf + µg = λ f + µ g.
(4)
Esta igualdad es una igualdad entre procedimientos: Para encontrar una primitiva de λf + µg,
hay que encontrar una primitiva de f , multiplicarla por λ y sumarle una primitiva de g
multiplicada por µ.
Ejemplo 1.
¶
Z
Z
Z
Z µ
√
√
1
dx
3
3
dx = 5 x dx + 3
=
xdx −
5x + 3 x −
2
cos x
cos2 x
2 3
1
5 · x4 + 3 · x 2 − tan x + C
4
3
Ejercicios:
3. Hallar las siguientes integrales indefinidas:
¢
R¡ 2
a)
3x − 2x + 1 dx
c)
R
b)
(a cos nx + b sin nx) dx
d)
d)
R
137
dx
x−a
R
R
(an xn + ... + a1 x + a0 ) dx
tan2 xdx
Capítulo 6. Integración
4. Reescribir la fórmula (4) en su versión con mención de la variable independiente.
Sustitución
A partir de la regla de la cadena:
d
f (g(x)) = f 0 (g (x)) g 0 (x) ,
dx
se deduce, simplemente por aplicación de (2), que
Z
f 0 (g (x)) g 0 (x) dx = f (g(x))
Por ejemplo, si deseamos calcular
Z
(5)
2
ex 2xdx
Haciendo f (u) = eu , g (x) = x2 , resulta f 0 (u) = eu y g 0 (x) = 2x. De modo que
Z
x2
e 2xdx =
Z
2
f 0 (g (x)) g 0 (x) dx = f (g(x)) = ex .
por (5). Nótese ahora qué sucede si el uso de la variable intermedia u es incorporado adentro
del signo integral. Es decir, si se hace la sustitución u = x2 ,
Z
2
ex 2xdx =
Z
eu
du
dx =
dx
Z
2
eu du = eu = ex
Hemos operado como si du
dx dx = du, "simplificando" dx, y todo funcionó bien. No es que simplificar como si fueran números a símbolos que sólo tienen un sentido en la expresión completa
sea correcto, pero la igualdad de las expresiones completas está garantizada por el procedimiento
anterior, basado en (5), y el resultado valida el método.
Ejemplo 2. Calculemos la integral
I=
Z
2x + 1
dx.
+x+1
x2
Haciendo la sustitución u = x2 + x + 1, resulta du
dx = 2x + 1. Nosotros nos
permitiremos escribir, sólo para su uso dentro del signo integral, du = (2x + 1) dx.
Entonces,
Z
¡
¢
1
du = ln u = ln x2 + x + 1 + C.
I=
u
La validez del resultado es en toda la recta, ya que x2 + x + 1 > 0 ∀x.
138
6.1 Integral indefinida
Ejercicio 5. Calcular las siguientes integrales
R
R
2
4
a) xex dx
b) x3 e−x dx
d)
g)
j)
m)
R
R
R
log x
x dx
e)
x
x+1 dx
h)
sen x
1+cos2 x dx
k)
R
cos 2x dx
R
n)
R
R
R
1
x(log x)n dx,
n∈Z
c)
f)
sin x cos x dx
i)
arctan x
1+x2 dx
l)
dx
x2 +a2
o)
R
R
R
R
¡
¢
x2 1 + x3 dx
e4x dx
sin2 x cos x dx
sin 2x dx
√ dx
a2 −x2
Integración por partes
Otra regla de derivación que provee un método de integración es la regla de derivación de
un producto. De
d
d
d
(f (x) · g (x)) =
f (x) · g (x) + f (x) ·
g (x)
dx
dx
dx
resulta
d
d
d
g (x) =
(f (x) · g (x)) − g (x) ·
f (x)
f (x) ·
dx
dx
dx
R d
Integrando miembro a miembro y usando la linealidad ( dx
h (x) dx = h (x) por definición),
Z
Z
d
d
g (x) dx = f (x) · g (x) − g (x) ·
f (x) dx, o bien,
(6a)
f (x) ·
dx
dx
Z
Z
f (x) · g 0 (x) dx = f (x) g (x) − g (x) f 0 (x) dx.
(6b)
El uso de variables dependientes y sustituciones formales también simplifica las fórmulas en
este caso. Poniendo
f (x) = u,
g (x) = v,
(7)
resulta
du
dx
= f 0 (x) ,
g 0 (x) dx =
dv
dx,
dx
dv
= g 0 (x) , o sea
dx
du
f 0 (x) dx =
dx
dx
Si volvemos a simplificar dx, (6) toma la forma
Z
Z
udv = uv − vdu.
(8)
Nuevamente, debe entenderse que las expresiones u, v, du y dv fueron definidas por (7) y
por
du = f 0 (x) dx,
dv = g 0 (x) dx
(9)
para su uso dentro del signo integral. Con esta definición, (8) se convierte en (6) y su uso queda
validado.
139
Capítulo 6. Integración
Ejemplo 3:
I=
Interpretando
½
ln x = u
dx = dv
Z
ln xdx
se deduce que
½
du = x1 dx
.
v=x
Luego, la aplicación de (8) da
Z
Z
Z
1
I = udv = uv − vdu = x ln x − x dx = x ln x − x.
x
Se puede comprobar el resultado obtenido derivando:
1
d
(x ln x − x) = ln x + x − 1 = ln x.
dx
x
Ejercicio 6: Hallar las integrales siguientes.
R
R
a) arcsin xdx
b) arctan xdx
d)
g)
R
R
(log x)2 dx
x cos xdx
e)
h)
R
R
x2 ex dx
x2 sin xdx
c)
f)
i)
R
e2x sin 3xdx
R
R
x sin xdx
x2 log x dx
Funciones racionales
Recordemos que una función racional es aquella que se escribe como cociente de dos polinomios. La integración de funciones racionales es esencialmente un problema algebraico. Si se
conocen todas las raíces del denominador, la función racional se puede descomponer en fracciones parciales, y éstas se integran con métodos muy simples. No nos parece interesante insistir
sobre este método, cuyo desarrollo el lector podrá encontrar en [1]. Para aplicarlo, es necesario
primero hallar la factorización del denominador, que implica calcular sus raíces. El cálculo de
las raíces de un polinomioha sido un tema de alta preferencia de los matemáticos. Es interesante
tener una somera idea de su historia. Por ejemplo una nota muy accesible se encuentra en [8].
Mostraremos aquí algunas ideas básicas y algunos ejemplos sencillos.
Ante todo, siempre se trabaja con "fracciones propias", esto es el grado del numerador estrictamente menor que el grado del denominador. Porque dada una función racional cualquiera
f (x) = P (x) ÁQ (x), se hace la división entera (ver ejemplo 8 en sección 3.1) P = QS + R
con gr (R) < gr (Q) Ahora
R
P
=S+ ,
Q
Q
donde el polinomio S es fácil de integrar. Veamos entonces los casos paradigmáticos.
1.
Z
dx
=
(x − a)n
½
(x − a)−n+1 si n 6= −1
.
ln (x − a) si n = 1
1
−n+1
140
6.1 Integral indefinida
2.
I=
Z
dx
= arctan x + C
+1
x2
(ejemplo 5 en la sección 4.2). Para potencias mayores se consiguen las integrales por
métodos recursivos que bajan el grado en una unidad. Por ejemplo, calculemos
3.
J=
Z
dx
(x2
+ 1)2
.
El truco consiste en volver a calcular I del caso 2, pero ahora por partes para que
aparezca J. Si ponemos
(
½
dx
du = (x−2x
u = x21+1
2 +1)2
=⇒
dx = dv
v=x
Luego,
x
+2
I= 2
x +1
Z
x2
dx.
(x2 + 1)2
(10)
Escribiendo x2 = x2 + 1 − 1,
Z
Z
Z
1
1
x2
dx
−
dx
=
dx = I − J.
2
2
x +1
(x2 + 1)
(x2 + 1)2
Sustituyendo en (10),
I=
x2
x
+ 2 (I − J) .
+1
Luego, ya que I = arctan x,
½
¾
½
¾
x
1
x
1
+I =
+ arctan x + C.
J=
2 x2 + 1
2 x2 + 1
4. Aquí entramos en la descomposición en fracciones parciales.
Z
1
I=
dx
(x − 2) (x − 3)
Buscamos constantes A, B tales que
A
B
1
+
=
x−2 x−3
(x − 2) (x − 3)
Efectuando la suma del miembro izquierdo
(A + B) x − (−3A − 2B)
Ax − 3A + Bx − 2B
=
(x − 2) (x − 3)
(x − 2) (x − 3)
e igualando al miembro derecho, como la igualdad de polinomios se da coeficiente a
coeficiente, deberá ser
½
A+B =0
.
3A + 2B = −1
Resuelto el sistema lineal surge que A = −1, B = 1. Luego
Z
Z
dx
x−3
dx
+
= ln (x − 3) − ln (x − 2) = ln
+ C.
I =−
x−2
x−3
x−2
141
Capítulo 6. Integración
5. Un último ejemplo:
I=
Z
x+1
dx.
(x − 1)2 (x − 2)
Ahora buscamos constantes A, B, C tales que
x+1
(x − 1)2 (x − 2)
B
C
A
+
+
2
x − 1 (x − 1)
x−2
=
A (x − 1) (x − 2) + B (x − 2) + C (x − 1)2
(x − 1)2 (x − 2)
(A + C) x2 + (−3A + B − 2C) x + (2A − 2B + C)
.
(x − 1)2 (x − 2)
=
=
El sistema de ecuaciones lineales es ahora de dimensión 3:

=0
 A+C
−3A + B − 2C = 1 .

2A − 2B + C
=1
La solución es A = −3, B = −2, C = 3. Por lo tanto,
Z
Z
Z
dx
dx
dx
I = −3
−2
=
+3
2
x−1
x−2
(x − 1)
1
+ 3 ln (x − 2) + C.
−3 ln (x − 1) + 2
x−1
Ejercicio 7: Calcular las siguientes integrales indefinidas.
R
R
dx
2x−3
2. (x−1)(x+7)
dx
1. (x−3)(x+2)
3.
R
dx
x2 −3x+2
4.
R
x+2
x2 +x dx
Una aplicación
Si en un intervalo, por ejemplo en un entorno del origen, dos funciones suficientemente
regulares satisfacen la relación
Z
f = F,
y se conoce el polinomio de Taylor T de grado n en 0 de f , valen las siguientes igualdades
en un intervalo que contiene al 0 :
F (k) (x) = f (k−1) (x) ,
T (k) (0) = f (k) (0) ,
k = 1, 2, ..., n + 1
k = 0, 1, ..., n.
Si ahora consideramos el polinomio
P =
Z
T,
P (0) = F (0) ,
142
6.2 Integral definida
valdrán las igualdades
P (k) (x) = T (k−1) (x) ,
k = 1, 2, ...
En particular,
½
P (k) (0) = T (k−1) (0) = f (k−1) (0) = F (k) (0) , k = 1, 2, ..., n + 1
,
P (0) = f (0)
de donde surge que P es el polinomio de Taylor de grado n + 1 de F en el origen.
Ejemplo: Para f (x) = 1/ (1 + x), hemos calculado su polinomio de Taylor de grado n
(ejercicio 13 del capítulo 5).
Tn (x) = 1 − x + x2 − · · · + (−1)n xn .
Tenemos, por un lado,
n+1
· · · + (−1)n xn+1
R
dx
1+x
= ln (1 + x) y, por el otro, P (x) =
R
Tn (x) dx = x −
x2
2
+ C. Con la condición P (0) = F (0) = 0, resulta C = 0. Por lo dicho,
x−
+
x3
3
−
xn+1
x2 x3
+
− · · · + (−1)n
2
3
n+1
es el polinomio de Taylor de ln (1 + x) en el origen. Haciendo y = 1 + x, se obtiene por otro
camino el desarrollo de ln en 1 :
ln y = (y − 1) −
6.2
(y − 1)n+1
(y − 1)2
+ · · · + (−1)n
+ Rn+1 .
2
n+1
Integral definida
En la sección anterior hemos visto algunas soluciones evidentes de búsqueda de funciones primitivas y, sobre esa base, hemos mostrado algunos métodos de cálculo que permiten encontrar
primitivas en otros casos menos evidentes. De todos modos, es claro que quedan muchas funciones a las que no podemos encontrarle primitiva y que se requiere una herramienta más
constructiva de éstas, seguramente con métodos no algebraicos. La solución a este problema no
es obvia y pasa por definir un método para calcular el área encerrada entre el gráfico de una
función y el eje de absisas, dentro de un intervalo. La construcción de ese método escapa a los
objetivos de este libro. Una excelente presentación se puede encontrar en el libro de Lipman
Bers [7]. El método de que estamos hablando es una operación que, fijado un intervalo [a, b],
permite asociar a cada función f de una cierta clase (la clase de las funciones integrables en
[a, b]), un número real
Z b
Z b
f=
f (x) dx,
f 7−→
a
a
el cual representa el área signada entre las cotas a y b, por los lados y entre el gráfico de f
y el eje x. La clase de las funciones integrables incluye a las funciones acotadas con un número
143
Capítulo 6. Integración
finito de discontinuidades en el intervalo.
+
+
a
b
figura 6.1
Ahora sí el objeto definido y denotado con dos signos alternativos (con y sin mención
de la variable independiente) es un número real y se llama integral definida de f entre a
y b. Por supuesto, el proceso de construcción de la integral es de gran importancia y en
él está la base para los métodos numéricos que permiten cálculos aproximativos.de su valor,
pero con sólo conocer las propiedades de esta nueva operación podremos resolver los principales
aspectos teóricos y encontrar su relación con el cálculo de primitivas. Luego, paradójicamente, el
cálculo de primitivas que desarrollamos en la sección anterior nos servirá para calcular integrales
definidas. Las propiedades de la integral definida admiten en todos los casos una referencia al
cálculo de áreas que ella resuelve y son fácilmente aceptables.
Propiedades de la integral definida
1. Linealidad: Si f y g son funciones integrables en el intervalo [a, b], también lo es
f + g y se tiene que
Z b
Z b
Z b
(f + g) =
f+
g.
(11)
a
a
a
De igual manera, si c es una constante, cf es integrable y
Z b
Z b
cf = c
f
a
(12)
a
2. Monotonía: Si f (x) ≤ g (x) para todo x ∈ [a, b] entonces
Z
b
a
f≤
Z
b
g.
(13)
a
3. Aditividad de dominio: Si a ≤ c ≤ b entonces
Z c
Z b
Z b
f=
f+
f
a
4.
a
Z
a
(14)
c
b
dx = b − a
144
(15)
6.2 Integral definida
Estas cuatro propiedades son evidentes tenida en cuenta la interpretación geométrica de la
integral. Todas las propiedades de la integral que usaremos se deducen de éstas. Veamos un
par de ejemplos y enseguida algunos ejercicios.
Ejemplos.
Ra
1. a f = 0 porque sigue de 3. que
Z a
Z a
Z
f=
f+
a
a
2.
a
f. Luego,
a
Z
a
f=
a
a
a
¯Z b ¯ Z b
¯
¯
¯
f ¯¯ ≤
|f |
¯
a
Z
a
La demostración es simple. (16) es equivalente a −
− |f | ≤ f ≤ |f | por (13).
f−
Z
a
f = 0.
a
(16)
Rb
a
|f | ≤
Rb
a
f ≤
Rb
a
|f | , que sigue de
Ejercicios:
8. Probar que
|f | ≤ M en [a, b]
⇒
¯Z b ¯
¯
¯
¯ ≤ M (b − a)
¯
f
¯
¯
a
9. (a) Ver que si f es una función continua en [a, b], el área (no el área signada) encerrada
Rb
entre el gráfico de f y el eje ”x” es a |f |
(b) Si f ≤ g en [a, b], el área encerrada entre los gráficos de ambas funciones dentro
Rb
de las cotas laterales x = a y x = b es a (g − f )
(c) El área encerrada entre los gráficos de las funciones f y g dentro de las cotas
Rb
laterales x = a y x = b es a |f − g|
a
a
b
b
a
fig. 6.2.a
b
fig. 6.2.b
fig. 6.2.c
Rb
Ra
10. Si a < b, definimos
b f = − a f . Sea ahora f una función integrable en [a, b] .
Probar que si x, y, z son tres puntos en cualquier orden en el intervalo [a, b], entonces
Rz
Ry
Rz
(a) x f = x f + y f .
Ry
Rz
Rz
(b) x f − x f = y f .
Veamos ahora cómo obtener (teóricamente) una primitiva de cualquier función continua en
un intervalo.
145
Capítulo 6. Integración
Teorema 1. (Teorema Fundamental del Cálculo).Sea f una función continua en
el intervalo [a, b] y definamos
F (x) =
Z
x
f (t) dt,
a≤x≤b
a
Entonces F es diferenciable en (a, b) con F 0 (x) = f (x).
Demostración:
1
F (x + h) − F (x)
=
h
h
Z
x+h
f (t) dt, (ejercicio 10.b)
x
mientras que
1
f (x) =
h
Z
x+h
f (x) dt
x
por (12) y (15). Luego, para h > 0,
¯Z x+h
¯
¯
¯
Z x+h
¯
¯
¯
¯ F (x + h) − F (x)
¯
− f (x)¯¯ = ¯¯
f (t) dt −
f (x) dt¯¯ =
¯
h
x
x
¯Z x+h
¯
Z x+h
¯
¯
1
¯
(f (t) dt − f (x)) dt¯¯ ≤
|f (x) − f (t)| dt
¯
h
x
x
h
→ 0.
≤
max |f (x) − f (t)|
h h→0
t∈[x,x+h]
El cálculo con h < 0 es similar ¥
Obsérvese que el TFC es teorema de existencia de la escuación diferencial más sencilla que
existe:
dy
= f (x)
dx
para f continua. El teorema de unicidad decía que F 0 = G0 en (a, b)
constante. Juntando ambos resultados,
⇒
F −G =
Teorema 2: Si f es continua y acotada en el intervalo (a, b) y x0 ∈ (a, b), existe
una única solución del problema
½
dy
dx
= f (x)
,
y (x0 ) = y0
dada por la función
y = y0 +
Z
x
f (t) dt.
x0
¥
Anunciamos el teorema 1 como una herramienta (teórica) provista por la integral definida
para encontrar primitivas. Veamos ahora cómo se da vuelta la tortilla y el cálculo de primitivas
sirve en la práctica para calcular integrales definidas.
El carácter de "primitiva" está definido para Rintervalos abiertos. Se extiende a intervalos
cerrados del siguiente modo:
R Diremos que F = f en [a, b] si existe un intervalo abierto
(c, d) ⊃ [a, b] tal que F = f en (c, d) .
146
6.2 Integral definida
Teorema 3. (Regla de Barrow)
Si f es continua
en [a, b] y F es cualquier primitiva de f en ese interval, o
R
sea si F = f en [a, b] , entonces
Z
b
f (x) dx = F (b) − F (a) .
a
Rx
Demostración: Poniendo G (x) = a f (t) dt, el TFC asegura que G es una
primitiva de f . Entonces, por el teorema de unicidad, existe una constante C
tal que G (x) − F (x) = C, ∀x ∈ [a, b]. Evaluando en x = a, como G (a) = 0,
C = −F (a) . Entonces G (x) = F (x) − F (a) ∀x ∈ [a, b] . En particular,
G (b) =
Z
b
a
f (x) dx = F (b) − F (a) .
¥
Para el cálculo de integrales definidas, se puede usar primero las técnicas de integrales
indefinidas (sustitución, integración por partes) y al final usar la regla de Barrow. Pero también
existen versiones de sustitución e integración por partes para integrales definidas:
Sustitución: Sea g una función con derivada continua en el intervalo [a, b] (g es de clase
C 1 en [a, b]). Sea f una función continua en la imagen de g. Entonces
Z
b
f [g (x)] g 0 (x) dx =
a
Z
g(b)
f (u) du
g(a)
Es decir, vale la sustitución u = g (x) y el correspondiente ”diferencial” du = g 0 (x) dx = du
dx dx
con la precaución de integrar entre los valores de la variable de integración u. Cuando x recorre
valores entre a y b, u = g (x) recorrerá valores entre g (a) y g (b) .
Ejemplo:
¯
Z π
Z 0
Z 1
1 3 ¯¯1
1
2
2
2
sin x cos xdx =
u du = −
u du = − u ¯ = −
π
3
3
1
2
0
0
con la sustitución u = sin x, du = cos xdx.
Integración por partes:
Z
a
Ejemplo:
Z
1
2
log xdx =
b
udv = uv|ba −
x log x|21
−
Z
1
2
Z
b
vdu
a
1
x dx = 2 log 2 − 1
x
Vía las sustituciones
u = log x ⇒ du =
dv = dx ⇒ v = x
147
1
dx
x
Capítulo 6. Integración
Ejercicios:
11. Calcular las siguientes integrales
R2
1)
3)
x5 dx
2)
sin xdx
4)
1
Rπ
−π
12. Calcular las siguientes integrales
Rπ
1) −π (sin x + cos x) dx
3)
R2
x
−1 e dx
13. Hallar el área entre las curvas y = x y y = x3.
R1
−1 x
Rπ
0
1
3
dx
cos xdx
2)
4)
R1
5
−1 2x dx
R3
2
−1 4x dx
14. Hallar el área entre la curva y = (x − 1) (x − 2) (x − 3) y el eje x.
15. Calcular las siguientes integrales
Rπ
1) 0 sin5 x cos xdx
2)
3)
R π2
0
¡ ¢
x sin 2x2 dx
Rπ
0
cos4 xdx
16. Calcular las siguientes integrales (usar el ejercicio 50 del capítulo 1)
R 2π
k∈Z
1) 0 sin kxdx,
2)
3)
4)
5)
6)
7)
R 2π
0
R 2π
0
R 2π
0
R 2π
0
R 2π
0
R 2π
0
coskxdx,
k∈Z
cosnx cos mxdx,
n, m ∈ Z, n, m ≥ 0
sinnx sin mxdx,
n, m ∈ Z, n, m ≥ 0
sinnx cos mxdx,
n, m ∈ Z, n, m ≥ 0
sin2 nxdx,
cos2 nxdx,
n ∈ Z, n ≥ 0
n ∈ Z, n ≥ 0
2
17. Hallar el área bajo la curva xe−x entre 0 y un número B > 0. ¿Tiende esta área
hacia un límite conforme B tiende hacia ∞?
18. Calcular las siguientes integrales
R2
1) 1 x3 log xdx
3)
R1
−1 xe
x dx
148
2)
R2√
x log xdx
1
6.3 Algunas aplicaciones
Comentarios sobre el origen de la notación
Dada la relación funcional y = f (x) , de llamar ∆x = h, el incremento sufrido por la
variable independiente y ∆y = f (x + ∆x) − f (x), surgió, al considerar el límite del cociente
incremental
∆y
= f 0 (x) ,
lim
∆x→0 ∆x
dy
el nombre dx
para ese límite.
Una forma de calcular el área bajo el gráfico de una función continua f entre las cotas
a y b, consiste en dividir el intervalo [a, b] por medio de una ”partición”. Se eligen n − 1
puntos intermedios y se divide el intervalo en n sub-intervalos:
a = x0 < x1 < ... < xn = b
La partición queda identificada por los puntos de subdivisión: P = {x0 , x1 , ..., xn }. Una medida
de su finura o precisión está dada por la ”norma de la partición: kP k = min (xi − xi−1 ). En
cada intervalo [xi−1 , xi ] se elige un punto cualquiera ξ i y se consideran las llamadas sumas
de Riemann
n
X
f (ξ i ) (xi − xi−1 )
(17)
i=i
Una representación gráfica ayuda a comprender el objeto de estas sumas
a
xi −1 ξ i xi
b
figura 6.3
Si se llama ∆xi = xi − xi−1 , la suma de Riemann (17) se puede reescribir
n
X
f (ξ i ) ∆xi
i=i
O bien, abreviadamente,
X
f (x) ∆x.
P
Pues bien, se prueba que
Z
a
b
f (x) dx = lim
kP k→0
X
f (x) ∆x.
P
Hecho que explica la notación y la existencia de la partícula dx en la integral.
149
Capítulo 6. Integración
6.3
Algunas aplicaciones
Cálculo de áreas. Ejemplo. área de un círculo de radio r. Se obtiene la mitad del área con
Z rr
Z rp
³ x ´2
2
2
r − x dx = r
1−
dx
I =
r
−r
−r
x
= sin t ⇒ dx = r cos tdt
r
Z arcsin(1)
Z arcsin(1)
1 + cos 2t
2
2
2
I = r
dt
cos tdt = r
2
arcsin(−1)
arcsin(−1)
)
( ¯π
¯π
¯2
1 ¯¯ 2
π
1
π
2
t¯ + sin 2t¯¯
= r
= + 0 = r2
2 −π
4
2
2
−π
2
2
Trabajo. Para una fuerza constante F que se desplaza a lo largo de un segmento [a, b],
el trabajo realizado por la fuerza se define como el producto F (b − a) . si la fuerza es
variable y ponemos el segmento en un sistema de coordenadas, digamos que el valor de la
→
−
fuerza en el punto x es F (x) (la componente de la fuerza en la dirección ab). Hecha
una partición P en [a, b] con puntos intermedios ξ i , una aproximación del trabajo en
todo el intervalo la da la suma de los trabajos en cada intervalito con fuerza constante
F (ξ) :
X
T =
F (ξ i ) ∆xi
Es razonable entonces definir el trabajo de la fuerza en el intervalo por
T =
Z
b
F (x) dx
a
Longitud de arco. Dada una curva descripta como gráfico de una función f , entre dos
extremos (a, f (a)) y (b, f (b)), tomada una partición P del intervalo [a, b], la longitud
de la poligonal que une los puntos (xi , f (xi )) es una buena aproximación de la longitud
de la curva.
∆y i
∆xi
xi −1
xi
figura 6.4
Para estimar la longitud de cada segmento de la poligonal, según el teorema de Pitágoras,
sirve el número
r
p
∆y 2
∆x2 + ∆y 2 = 1 +
∆x
∆x2
150
6.3 Algunas aplicaciones
que da una longitud total
X
s
1+
µ
∆y
∆x
¶2
∆x.
Cuando la norma de la partición tiende a cero, esta suma se convierte en
s
µ ¶2
Z b
dy
L=
1+
dx
dx
a
Ejemplo. Longitud de la semicircunderencia de radio r con centro en el origen.
p
y = f (x) = r2 − x2 entre − r y r
· ¸2
µ ¶2
dy
−x
dy
x2
dy
r2
1
= √
,
= 2
,
1
+
=
=
¡ ¢2
2
2
2
2
2
dx
dx
r −x
dx
r −x
r −x
1 + xr
Z 1
1
1
q
q
dx
=
rdu =
¢
¡
2
x 2
−r
−1
1+ r
1 + (u)
³π π ´
= r arcsin u|1−1 = r
+
= πr.
2
2
L =
Z
r
Ejercicios:
19. Hallar la longitud del gráfico de y =
resultados del capítulo 1.
√
r2 − x2 para r cos θ ≤ x ≤ r. Comparar con los
20. Un resorte tiene 45cm de largo y se necesita una fuerza de 5kgr para mantenerlo comprimido a una longitud de 40cm. Si la fuerza está dada como f (x) = kx, donde k es
una constante y x es el decrecimiento en la longitud, ¿cuál es la constante k?. Cuánto
trabajo se realiza al comprimir el resorte de 40cm a 30cm?
21. Una partícula atrae a otra con una fuerza inversamente proporcional al cuadrado de la
distancia que las separa. Sea C la constante de proporcionalidad. Si ponemos el origen de
coordenadas en la primer partícula, cuánto trabajo trabajo se realiza al mover la segunda
partícula a lo largo de una recta, alejándola de la primera desde una distancia r1 hasta
una distancia r > r1 ?
151
Capítulo 6. Integración
Referencias
[1] Serge Lang, Cálculo, Addison Wesley Iberoamericana (1990).
[2] Michael Sullivan, Precálculo - 4ta. Edición - Prentice Hall (1996).
[3] Michael Spivak, Calculus, 2a Edición, Reverté S.A. (1992).
[4] G. Thomas y R. Finney, Cálculo con Geometría Analítica vol I, Addison - Wesley
Iberoamericana (1977).
[5] A. Aragón, J. Pinasco, C. Schifini y A. Varela, Introducción a la Matemática, U.N.G.S.
(2006).
[6] R. Courant y F. John, Introducción al Cálculo y al Análisis Matemático, Limusa (1974).
[7] L. Bers, Calculus, Holt, Rinehart and Winston; 2d ed edition (1976)
[8] J. Rey Pastor, P. Pi Calleja y C. A. Trejo, Análisis Matemático I, Kapelusz (1952).
[9] W. Rudin, Principios de Análisis Matemático, Mc. Graw Hill (1966).
[10] Creighton Buck, Cálculo Superior, Mc. Graw Hill (1969).
152