Cateto Cateto Hipotenusa Ángulo recto 3cm 4cm 5cm Estudia la

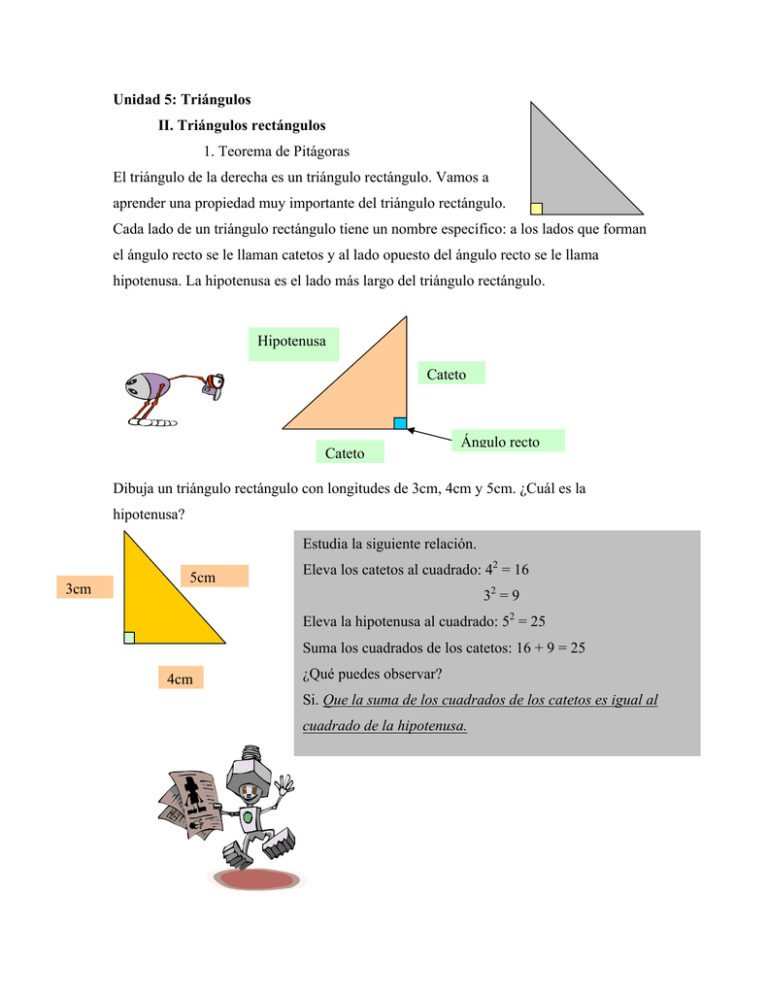
Unidad 5: Triángulos
II. Triángulos rectángulos
1. Teorema de Pitágoras
El triángulo de la derecha es un triángulo rectángulo. Vamos a
aprender una propiedad muy importante del triángulo rectángulo.
Cada lado de un triángulo rectángulo tiene un nombre específico: a los lados que forman
el ángulo recto se le llaman catetos y al lado opuesto del ángulo recto se le llama
hipotenusa. La hipotenusa es el lado más largo del triángulo rectángulo.
Hipotenusa
Cateto
Cateto
Ángulo recto
Dibuja un triángulo rectángulo con longitudes de 3cm, 4cm y 5cm. ¿Cuál es la
hipotenusa?
Estudia la siguiente relación.
3cm
5cm
Eleva los catetos al cuadrado: 42 = 16
32 = 9
Eleva la hipotenusa al cuadrado: 52 = 25
Suma los cuadrados de los catetos: 16 + 9 = 25
4cm
¿Qué puedes observar?
Si. Que la suma de los cuadrados de los catetos es igual al
cuadrado de la hipotenusa.
Es precisamente esa la relación que vamos a utilizar en esta lección conocida como el
Teorema de Pitágoras.
El Teorema de Pitágoras:
En un triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado
de la hipotenusa.
Se puede expresar en símbolos de la siguiente forma. Vamos a dejar que la longitud de
los catetos esté representada por a y b. La hipotenusa con una c.
c
a
a2 + b2 = c2
a y b son los catetos.
c es la hipotenusa
b
Ejemplos:
1) Halla la medida de la hipotenusa si la medida de los catetos es 6cm y 8cm.
Como es un triángulo rectángulo, solo sustituimos en la fórmula del teorema: a2 + b2 = c2.
a=6
b=8
c=?
62 + 82 = c2
36 + 64 = c2
100 = c2
100 = c
10 = c
Sustituir en el Teorema de Pitágoras
Elevar al cuadrado cada longitud
Efectuar la suma
Calcular la raíz cuadrada. (Una calculadora
puede ser útil.)
2) Si la longitud de la hipotenusa es 13m y la de uno de los catetos es 12m, halla la
medida del otro cateto.
a = 12
b=?
c = 13
122 + b2 = 132
144 + b2 = 169
b2 = 169 – 144
b2 = 25
b = 25
b=5
Sustituir en el Teorema de Pitágoras
Elevar al cuadrado cada longitud
Restamos 144 para dejar la b solo
Calcular la raíz cuadrada. (Una calculadora
puede ser útil.)
3) Halla la longitud del lado que falta.
a2 + b2 = c2
152 + 182 = c2
c
15m
225 + 324 = c2
549 = c2
549 = c
18m
4)
6m
23.43 = c
b
12m
62 + b2 = 122
36 + b2 = 144
b2 = 144 – 36
b2 = 108
b = 108
b = 10.39
Una calculadora es útil para hacer estas
aproximaciones.