Cálculo Diferencial - Aprende Matemáticas

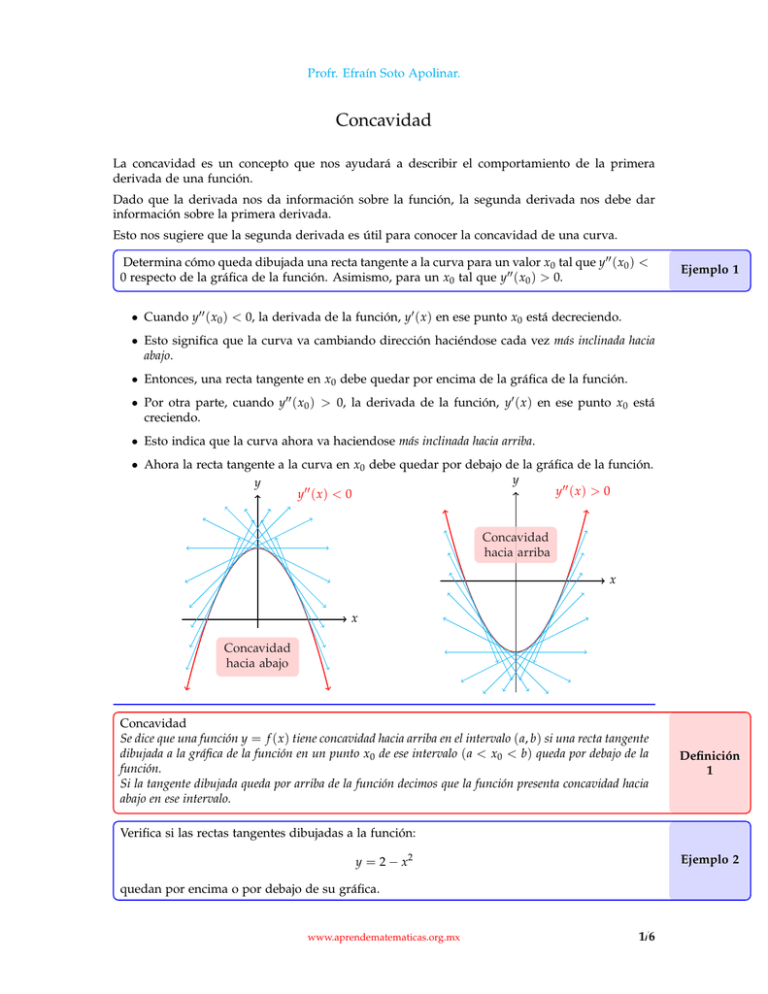
Profr. Efraín Soto Apolinar.
Concavidad
La concavidad es un concepto que nos ayudará a describir el comportamiento de la primera
derivada de una función.
Dado que la derivada nos da información sobre la función, la segunda derivada nos debe dar
información sobre la primera derivada.
Esto nos sugiere que la segunda derivada es útil para conocer la concavidad de una curva.
Determina cómo queda dibujada una recta tangente a la curva para un valor x0 tal que y00 ( x0 ) <
0 respecto de la gráfica de la función. Asimismo, para un x0 tal que y00 ( x0 ) > 0.
Ejemplo 1
• Cuando y00 ( x0 ) < 0, la derivada de la función, y0 ( x ) en ese punto x0 está decreciendo.
• Esto significa que la curva va cambiando dirección haciéndose cada vez más inclinada hacia
abajo.
• Entonces, una recta tangente en x0 debe quedar por encima de la gráfica de la función.
• Por otra parte, cuando y00 ( x0 ) > 0, la derivada de la función, y0 ( x ) en ese punto x0 está
creciendo.
• Esto indica que la curva ahora va haciendose más inclinada hacia arriba.
• Ahora la recta tangente a la curva en x0 debe quedar por debajo de la gráfica de la función.
y
y
y00 ( x ) > 0
y00 ( x ) < 0
Concavidad
hacia arriba
x
x
Concavidad
hacia abajo
Concavidad
Se dice que una función y = f ( x ) tiene concavidad hacia arriba en el intervalo ( a, b) si una recta tangente
dibujada a la gráfica de la función en un punto x0 de ese intervalo ( a < x0 < b) queda por debajo de la
función.
Si la tangente dibujada queda por arriba de la función decimos que la función presenta concavidad hacia
abajo en ese intervalo.
Definición
1
Verifica si las rectas tangentes dibujadas a la función:
y = 2 − x2
Ejemplo 2
quedan por encima o por debajo de su gráfica.
www.aprendematematicas.org.mx
1/6
Profr. Efraín Soto Apolinar.
• Volvemos a retomar el ejemplo de la página ??.
• Ya sabemos que la primera derivada de esta función es: y0 ( x ) = −2 x
• Mientras que la segunda derivada es: y00 ( x ) = −2.
• Observa que la segunda derivada es negativa siempre.
• Esto nos dice que la pendiente de las rectas tangentes van decreciendo conforme x crece.
• Es decir, la gráfica de la función tiene concavidad hacia abajo, dado que las rectas tangentes
van quedando por encima de la gráfica de la función:
y
3
2
1
x
−2
−1
2
1
−1
y = 2 − x2
−2
Indica la concavidad en cada uno de los puntos críticos de la siguiente función:
Ejemplo 3
y = 3 x4 − 20 x3 + 12 x2 + 96 x − 10
• Tenemos que calcular todos los puntos críticos de esta función.
• Empezamos calculando su derivada:
dy
dx
= 12 x3 − 60 x2 + 24 x + 96
= 12 · x3 − 5 x2 + 2 x + 8
Profesor:
Si se requiere,
sugiera estudiar
extra-clase
la
• Observa que la derivada se hace cero para x = −1.
• Entonces, podemos dividir entre x + 1 la derivada para factorizarla:
−5 2
8
−1 6 −8
1 −6 8
0
1
división sintética.
−1
www.aprendematematicas.org.mx
2/6
Profr. Efraín Soto Apolinar.
• Esto nos permite reescribir la derivada de la siguiente forma:
dy
= 12 · ( x + 1) x2 − 6 x + 8
dx
= 12 · ( x + 1)( x − 4)( x − 2)
• Ahora fácilmente podemos calcular los puntos críticos de la función igualando a cero cada
factor.
• Es decir, los puntos críticos de la función son: x1 = −1, x2 = 4, y x3 = 2.
• Para conocer la concavidad en cada uno de ellos, vamos a calcular la segunda derivada y a
evaluarla en cada punto crítico:
d2 y
= 36 x2 − 120 x + 24
dx2
• Al evaluarla en x = x1 = −1, obtenemos:
d2 y = 36 (−1)2 − 120 (−1) + 24 = 180 > 0
dx2 x =−1
• Entonces, en este punto tiene un mínimo, y por tanto, tiene concavidad hacia arriba.
• Para el siguiente punto crítico tenemos:
d2 y = 36 (2)2 − 120 (2) + 24 = −72 < 0
dx2 x =2
que nos indica que la función tiene un máximo ahí y concavidad hacia abajo.
• Para x = x3 = 4, obtenemos:
d2 y dx2 = 36 (4)2 − 120 (4) + 24 = 120 > 0
x =4
por lo que la función tiene un mínimo en ese punto crítico y concavidad hacia arriba.
• La siguiente gráfica muestra toda esta información:
y
500
y = 3 x4 − 20 x3 + 12 x2 + 96 x − 10
400
300
200
100
−3
−2
−1
x
1
2
3
4
5
6
−100
www.aprendematematicas.org.mx
3/6
Profr. Efraín Soto Apolinar.
En el ejemplo anterior hemos visto que la concavidad cambió, empezando la función con concavidad hacia arriba, luego hacia abajo y termina con concavidad hacia arriba de nuevo.
Una buena pregunta que debemos hacer ahora es cómo reconocer en qué punto deja de tener
concavidad hacia arriba y empieza a tener concavidad hacia abajo.
Eso debe ocurrir en el punto en que la derivada deja de crecer y empieza a decrecer. Es decir,
debe ocurrir en el punto xc en el cual la segunda derivada se hace cero.
Calcula los intervalos donde la función:
y = 3 x4 − 20 x3 + 12 x2 + 96 x − 10
Ejemplo 4
tiene concavidad hacia arriba y donde tiene concavidad hacia abajo.
• Para calcular los intervalos debemos conocer exactamente dónde cambia la concavidad de
la función.
• Es decir, en qué punto cambia de signo su segunda derivada.
• En el ejemplo anterior calculamos los puntos críticos de la función, como su concavidad en
cada uno de ellos.
• Entonces, calculamos su segunda derivada:
d2 y
= 36 x2 − 120 x + 24
dx2
• Ahora vamos a igualarla a cero y vamos a resolver para x:
√
−b ± b2 − 4 ac
x =
2a p
−(−120) ± (−120)2 − 4 (36)(24)
=
2 (36)
p
120 ± 14400 − (3456)
=
√ 72
120 ± 10944
=
72
• Lo que puede reescribirse como:
√
√
120 ± 24 19
5 ± 19
x=
=
72
3
• Esto es,
x1 =
5+
√
3
19
≈ 3.1196
y
x2 =
5−
√
3
19
≈ 0.2137
• Estos dos puntos son los límites donde la función cambia de concavidad.
• Entonces, los intervalos donde la función presenta concavidad hacia arriba son: (−∞, 0.2137),
y (3.1196, ∞).
www.aprendematematicas.org.mx
4/6
Profr. Efraín Soto Apolinar.
• Y el intervalo donde la función tiene concavidad hacia abajo es: (0.2137, 0.31186).
• Este resultado se verifica visualmente en la gráfica de la función.
Punto de inflexión
Sea y = f ( x ) una función con segunda derivada definida en x0 . El punto x0 es un punto de inflexión si
f 00 ( x0 ) = 0.
Definición
2
En otras palabras, un punto de inflexión es aquel punto donde la concavidad de la función cambia.
Calcula todos los puntos de inflexión de la función:
y = e− x
Ejemplo 5
2
• Empezamos calculando la segunda derivada de la función:
dy
dx
d2 y
dx2
2
= −2 xe− x
2
=
4 x2 − 2 · e− x
• Para que la segunda derivada se haga cero, es necesario que 4 x2 − 2 = 0 luego:
4 x2
x
2
x
⇒
= 2
1
=
2
=
⇒
√
1
2
±√ = ±
≈ 0.7071
2
2
• Ahora es fácil localizar en la gráfica los puntos de inflexión de esta función:
y
1
0.8
0.6
0.4
0.2
y = e− x
−3
−2
1
−√
2
1
√
2
2
3
2
x
√
√
• Los intervalos con diferente
√
√ concavidad son: (−∞, −1/ 2) y (1/ 2, ∞) con concavidad
hacia arriba y (−1/ 2, 1/ 2) con concavidad hacia abajo.
www.aprendematematicas.org.mx
5/6
Profr. Efraín Soto Apolinar.
Créditos
Albert
Einstein
Todo debe hacerse tan simple como sea posible, pero no más.
Este material se extrajo del libro Matemáticas I escrito por Efraín Soto Apolinar. La idea es compartir estos trucos para que más gente se enamore de las matemáticas, de ser posible, mucho más
que el autor.
Autor: Efraín Soto Apolinar.
Edición: Efraín Soto Apolinar.
Composición tipográfica: Efraín Soto Apolinar.
Diseño de figuras: Efraín Soto Apolinar.
Productor general: Efraín Soto Apolinar.
Año de edición: 2010
Año de publicación: Pendiente.
Última revisión: 01 de agosto de 2010.
Derechos de autor: Todos los derechos reservados a favor de Efraín Soto Apolinar. México. 2010.
Espero que estos trucos se distribuyan entre profesores de matemáticas de todos los niveles y sean
divulgados entre otros profesores y sus alumnos.
Este material es de distribución gratuita.
Profesor, agradezco sus comentarios y sugerencias a la cuenta de correo electrónico:
[email protected]
www.aprendematematicas.org.mx
6/6