POSICIONES DE RECTAS Y PLANOS EN EL ESPACIO Se estudia

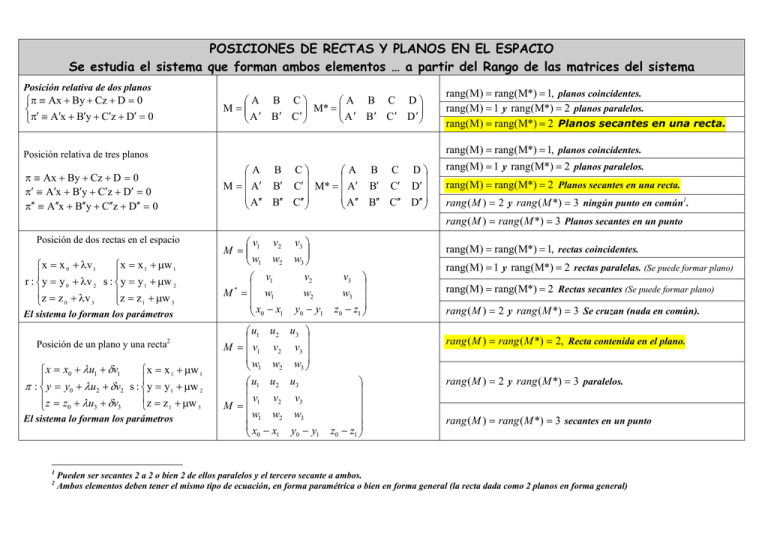
POSICIONES DE RECTAS Y PLANOS EN EL ESPACIO
Se estudia el sistema que forman ambos elementos … a partir del Rango de las matrices del sistema
Posición relativa de dos planos
⎧π ≡ Ax + By + Cz + D = 0
⎨
⎩π′ ≡ A′x + B′y + C′z + D′ = 0
⎛A B C⎞
⎛A B C D⎞
⎟⎟ M* = ⎜⎜
⎟⎟
M = ⎜⎜
⎝ A ′ B′ C ′ ⎠
⎝ A ′ B′ C ′ D ′ ⎠
rang(M ) = rang(M*) = 1, planos coincidentes.
rang(M ) = 1 y rang(M*) = 2 planos paralelos.
rang(M ) = rang(M*) = 2 Planos secantes en una recta.
rang(M ) = rang(M*) = 1, planos coincidentes.
Posición relativa de tres planos
⎛A B C⎞
⎛A B C D⎞
⎜
⎟
⎜
⎟
M = ⎜ A′ B′ C′ ⎟ M* = ⎜ A′ B′ C′ D′ ⎟
⎜ A′′ B′′ C′′ ⎟
⎜ A′′ B′′ C′′ D′′ ⎟
⎝
⎠
⎝
⎠
π ≡ Ax + By + Cz + D = 0
π′ ≡ A′x + B′y + C′z + D′ = 0
π′′ ≡ A′′x + B′′y + C′′z + D′′ = 0
rang(M ) = 1 y rang(M*) = 2 planos paralelos.
rang(M ) = rang(M*) = 2 Planos secantes en una recta.
rang ( M ) = 2 y rang ( M *) = 3 ningún punto en común1.
rang ( M ) = rang ( M *) = 3 Planos secantes en un punto
Posición de dos rectas en el espacio
⎧ x = x 0 + λv 1
⎧x = x 1 + μw 1
⎪
⎪
r : ⎨ y = y 0 + λv 2 s : ⎨ y = y 1 + μw 2
⎪z = z + λ v
⎪z = z + μw
1
3
0
3
⎩
⎩
El sistema lo forman los parámetros
2
Posición de un plano y una recta
⎧ x = x0 + λu1 + δv1
⎧x = x 1 + μw 1
⎪
⎪
π : ⎨ y = y0 + λu2 + δv2 s : ⎨ y = y 1 + μw 2
⎪ z = z + λu + δv
⎪z = z + μw
1
3
0
3
3
⎩
⎩
El sistema lo forman los parámetros
1
2
⎛ v v2 v3 ⎞
⎟⎟
M = ⎜⎜ 1
⎝ w1 w2 w3 ⎠
v2
⎛ v1
⎜
*
M = ⎜ w1
w2
⎜x − x y − y
0
1
⎝ 0 1
⎛ u1 u2 u3 ⎞
⎟
⎜
M = ⎜ v1 v2 v3 ⎟
⎜w w w ⎟
2
3⎠
⎝ 1
⎛ u1 u2 u3
⎜
⎜ v v2 v3
M =⎜ 1
w w2 w3
⎜ 1
⎜x − x y − y
0
1
⎝ 0 1
rang(M ) = rang(M*) = 1, rectas coincidentes.
⎞
⎟
w3 ⎟
z0 − z1 ⎟⎠
v3
rang(M ) = 1 y rang(M*) = 2 rectas paralelas. (Se puede formar plano)
rang(M ) = rang(M*) = 2 Rectas secantes (Se puede formar plano)
rang ( M ) = 2 y rang ( M *) = 3 Se cruzan (nada en común).
rang ( M ) = rang ( M *) = 2, Recta contenida en el plano.
⎞
⎟
⎟
⎟
⎟
z0 − z1 ⎟⎠
rang ( M ) = 2 y rang ( M *) = 3 paralelos.
rang ( M ) = rang ( M *) = 3 secantes en un punto
Pueden ser secantes 2 a 2 o bien 2 de ellos paralelos y el tercero secante a ambos.
Ambos elementos deben tener el mismo tipo de ecuación, en forma paramétrica o bien en forma general (la recta dada como 2 planos en forma general)