fuerza 2d

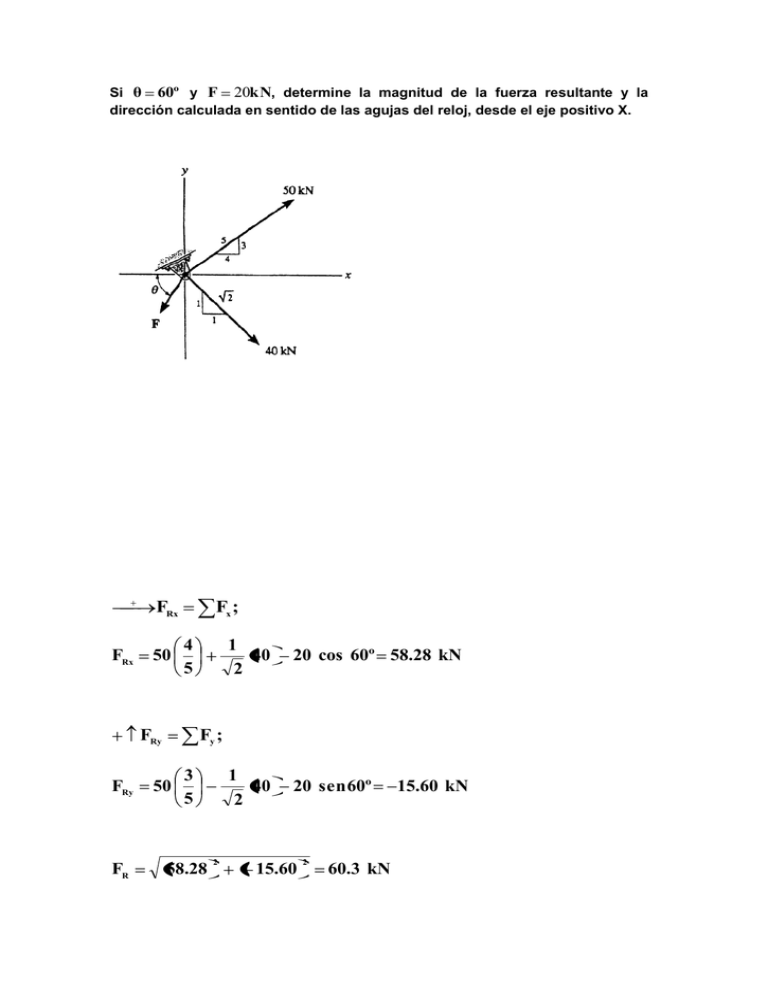
Si θ 60º y F 20kN, determine la magnitud de la fuerza resultante y la
dirección calculada en sentido de las agujas del reloj, desde el eje positivo X.
FRx
FRx
50
Fx ;
4
5
FRy
FRy
FR
1
40
2
20 cos 60º 58.28 kN
1
40
2
20 sen 60º
Fy ;
50
3
5
58.28
2
15.60
2
60.3 kN
15.60 kN
θ tan
1
15.60
58.28
15.0º
Determine las componentes X y Y de F1 y F2 .
F1y
200 cos 45º
141 N
F2x
150 cos 30º
130 N
F2y
150 sen 30º
75 N
Tres fuerzas actúan en el enganche . Determine la magnitud y dirección de
en F1 de
manera que la fuerza resultante sea dirigida a lo largo de la axisa X’ (+) y tenga una
magnitud de 1 KN.
→FRx+ =
1000
)
:
+F1
cos(
-1000
F1
F1 cos (
= 818.198
) = 347.827
+
F1 = 889 N
La fuerza de 500 lb actuando en la estructura va a ser resuelta en dos componentes
actuando a través de la axisa del lado AB y AC. Si el componente de la fuerza a través de AC
es requerida a ser 300 lb, dirigida desde A a C, determine la magnitud de la fuerza actuante
a través de AB y el ángulo
de la fuerza de 500 lb.
Utilizaremos la ley del paralelogramo
Trigonometría: Usando la ley de los senos:
= 0.5796
=
=
=
FAB = 485 lb
Determine el ángulo de concepción de los puntales de AB y AC de
modo que la fuerza horizontal de 400 libras tiene una
componente de 600 libras, que actúa a la izquierda, en la misma
dirección de B hacia A tomar
Paralelogramo la ley: la ley de paralelogramo además se muestra en la fig. (A).
Trigonometría: utilizando la ley del coseno fig. (b), tenemos
El ángulo Ø puede ser determinado utilizando la ley de los senos fig. (b).
Las fuerzas actuando sobre el diente del engranaje es F = 20 lb. Resuelva esta
fuerza dentro de dos componentes actuando entre las líneas aa y bb,
Usamos el método del rectángulo para resolver el problema
Si
y
, determine la magnitud y orientación, medida
desde el eje x positivo, de la fuerza resultante de las tres fuerzas que
actúan sobre el anaquel.
Sumamos algebraicamente las componentes de las fuerzas, de donde:
;
;
La magnitud de la fuerza resultante
El ángulo de dirección
es:
medido en sentido horario desde el eje x positivo es
Determine la magnitud y orientación
de
para que la fuerza de la
resultante se dirija a lo largo del eje “Y” positivo y tiene una magnitud de
1500 N
En notación escalar: sumamos todos los componentes de las fuerzas algebraicamente
tanto en el eje “X” como en el eje “Y” y obtenemos que:
Como estamos en el eje de las X positivas:
(1)
Como el eje de las “Y” es positivo también nos queda:
Como ya resolvimos (1) y (2) obtenemos que:
Determine la magnitud y orientación, mida en sentido contrario a las manecillas del reloj
desde el eje Y positivo, (en función a la fuerza resultante), FB = 600N y θ = 200.
Notación escalar: resumen de las componentes de fuerzas algébricas.
La magnitud de la fuerza resultante FR es
La dirección del ángulo θ medida en sentido contrario a las manecillas del reloj desde el eje Y
positivo es
La viga se izó con dos cadenas. Si la fuerza resultante se dirige 600N lo
largo del eje y positivo, determinar las magnitudes de las fuerzas FA y FB
actuar en cada cadena y la orientación θ de FB de manera que la
magnitud de θ un mínimo. FA actúa a 300 en el eje y como se muestra.
Un mínimo de FB
Determine la amplitud del ángulo (
) para el lado AB de manera que la
fuerza horizontal de 400 lb tenga un componente de 500 lb dirigido desde A alrededor de
C. ¿Cuál es la compone de fuerza actuendo a través del miembro AB ?. Tome
Utilizaremos la ley del paralelogramo
Trigonometría: Usando la ley de los senos:
= .8035
=
=
Usando la ley de los senos obtenemos:
=
.
FAB = 621 lb
La componente de la fuerza F que actúa a lo largo de la línea AA es que se
requieren 30 libras, determinar la magnitud de F y sus componentes a lo largo
de la línea BB.
f=19.6 lb R//
Fb=26.4 lb R//
Exprese F1 y F2 como vectores cartesianos.
Determine la x y componentes de la fuerza de 800-lb
Fx=800sen40º=514lb
Fy=-800cos40º=-613lb
Determinar el ángulo θ entre la bordea dora de la hoja de soporte de metal
Descomponga la fuerza de 50lb en componentes. (a) a lo largo del eje x y eje
y, (b) eje x y eje y prima.
a) DCL
Mediante un triangulo de fuerzas.
b) DCL
Fx
50lbCos45
Fx
35.4lb
Fy
50lbSen30
Fy
35.4lb
sen 15
Fx
sen 45
Fy
sen 120
50lb
sen 120
50lb
Fx 14.9lb
Fy
40.8lb
Exprese cada una de las tres fuerzas como un vector cartesiano respecto al
aje x y eje y. Determine la magnitud y dirección de F1 sabiendo que la
resultante de la fuerza X prima positiva tiene una magnitud de FR=600N.
Expresado de manera Cartesiana.
F1 ( F1 cos i F1 sen j)N
F2
(350 i ) N
F3
( 100 j ) N
Aplicando Definicion de Fuerza Resultante.
FR
FR
(600cos30)i (600sen30)j
519.61i 300j
FR
F
Igualando componentei y j
519.6 F1 cos
350
F1 cos
300
169.6
F1 sen
F1 sen
F1
100
400
400
2
(169.6) 2
F1
434.4 N Respuesta
Direccion de F1
Tan
1
400
169.6
67.2 Respuesta
Determine la magnitud y dirección de la resultante
las tres fuerzas encontrando primero la resultante F´=F2+F3
formación FR=F´+F1.
= 23.53º - 21.15º = 2.37º
de
y la
Tres cables se ponen el tubo tal que ellos crean una fuerza consiguiente
que tiene una magnitud de 900 libras. Si dos de los cables son sujetados
a fuerzas conocidas, como se muestra en la figura, determine la
dirección θ de los terceros cables de modo que la magnitud de fuerza F
en los cables sea mínima. Todos mienten en fuerzas del avión x-y.
¿Cuál es la magnitud de F?
SUGERENCIA: primero se encuentra la resultante de las dos fuerzas
conocidas.
F´=
F= 900 – 802.64 = 97.4 lb Ans
=
;
Determine la magnitud de la fuerza consiguiente y su dirección, medida
en contrario del eje X positivo.
FRX =
FX;
FRX = (850) – 625 sin 30º - 750 sin 45º = -162.8 N
+ FRY =
FY;
FRY = (850) – 625 cos 30º - 750 cos 45º = -520.9 N
FR =
= tan-1 [
= 546 N
] = 72.64º
= 180º + 72.64º = 253º
Determinar la magnitud de la fuerza resultante y su dirección medida hacia la
izquierda desde el eje x positivo.
Si
, determinar la de ángulos y para que la fuerza resultante se
dirige a lo largo del eje x positivo y tiene una magnitud de
.
El carro debe ser remolcado usando dos cuerdas. Determine la magnitud de
fuerzas Fa y el Fb que actúa en cada cuerda adentro orden para desarrollar
un forcé resultante de 950N directo a lo largo del eje positivo de X. Sen ѳ=5
Ley del Paralelogramo: el paralelogramo como se muestra en la figura (a).
Trigonometría: Usando la figura (b)
El camión es remolcado mediante dos cuerdas. Si la fuerza resultante es
, dirigida a lo
largo del eje X positivo. Determinar las magnitudes de las fuerzas y
que actúan en cada
cuerda y el ángulo de
donde la magnitud de
es mínima.
Actúa en
desde el
eje X, como se muestra.
Ley paralelogramo: Para producir una fuerza mínima
, ha de actuar de forma
perpendicular a la ley de paralelogramo . La adición es mostrada en la Fig. (a)
Resolver el problema 2.41, sumando el rectángulo ó las componentes X,Y de la fuerza para
obtener la fuerza resultante.
Determinar el ángulo para la conexión de un miembro de la placa para
que la fuerza resultante de la FA y FB se dirige horizontalmente a la
derecha. También, ¿cuál es la magnitud de la fuerza resultante.
Ley del paralelogramo: La ley del paralelogramo se muestra en la fig. (A).
Trigonometría: Ley de Uso de los senos [fig. (B)].
hemos
A partir del triángulo = 180 - (90-54.93) -50 =
94.93.Asi, utilizando la ley, la magnitud de Fr.
Dos fuerzas se aplican en el extremo de un tornillo en el ojo para
eliminar el post. Determine el ángulo (0 <beta <90) y la magnitud de la
fuerza F para que la fuerza resultante que actúa sobre el puesto está
dirigido verticalmente hacia arriba y tiene una magnitud de 750N
Ley del paralelogramo: La ley del paralelogramo se muestra en Finlandia. (A).
Trigonometría: Ley de Uso de los senos [fig. (B)]. que tenemos.
Asi.
El resorte tiene una tiesura de k = 800 N/m y una longitud de 200 mm.
Determina la fuerza en los cables BC y BD cuando el resorte se sostiene
en la posición mostrada
La fuerza en el resorte: El resorte estirado
Aplicando 3-2, tenemos
Ecuaciones de equilibrio:
(1)
(2)
Sustituyendo Eqs. (1) y (2) produce:
Determine la magnitud de la fuerza resultante
y su dirección,
medido en sentido contrario a las agujas del reloj del eje x positivo.
Determine el ángulo θ (θ < 90º) entre los dos pavoneos para que las 500 lb
de la fuerza horizontal tenga una componente de 600 lb dirigida de A
hacia C. ¿Cuál es la componente de fuerza que está actuando a lo largo
del miembro BA?
Ley del paralelogramo: La ley del paralelogramo de
suma se muestra en Fig. a
Trigonometría: Usando la ley de los cosenos (fig.
b), tenemos:
El ángulo θ (θ < 90º) lo podemos determinar usando la
ley de los senos (fig. b)
El camión para ser remolcado con dos cuerdas, determinar la magnitud de las fuerzas de la FA
y FB que actúa sobre cada cuerda con el fin de desarrollar una fuerza resultante de 950 N
dirigida a lo largo del eje x positivo Set = 50.
La ley del paralelogramo: la ley del paralelogramo se muestra en la fig. (A)
Trigonometría: el uso de ley de los senos fig. (b), tenemos
El Logis remolcado por dos tractores A y B. Determinar la magnitud de las dos fuerzas de
arrastre FA y FB, si es necesario que la fuerza resultante tiene una magnitud P.= 10 kN y se
dirigió
a
lo
largo
del
eje
x.
Set
θ
=
15
º.
a ley del paralelogramo: La ley del paralelogramo se muestra en la figura (a)
Trigonometría: Uso de ley de los senos (Fig.), hemos
fA= 3.66 kn R//
fb= 7.07kn R//